Шум или ошибка — основная проблема в сигнале, которая нарушает надежность системы связи. Кодирование с контролем ошибок — это процедура кодирования, выполняемая для контроля появления ошибок. Эти методы помогают в обнаружении ошибок и исправлении ошибок.
Существует много различных кодов, исправляющих ошибки, в зависимости от применяемых к ним математических принципов. Но исторически эти коды были классифицированы на линейные блочные коды и коды свертки .
Линейные Блочные Коды
В линейных блочных кодах биты четности и биты сообщения имеют линейную комбинацию, что означает, что результирующее кодовое слово является линейной комбинацией любых двух кодовых слов.
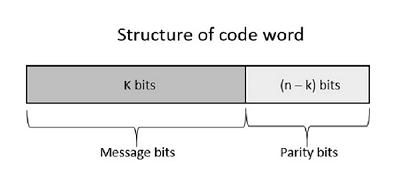
Рассмотрим некоторые блоки данных, которые содержат k битов в каждом блоке. Эти биты отображаются с блоками, которые имеют n битов в каждом блоке. Здесь n больше, чем k . Передатчик добавляет избыточные биты, которые являются (nk) битами. Отношение k / n является скоростью кода . Обозначается через r, а значение r равно r <1 .
Добавленные здесь биты (nk) являются битами четности . Биты четности помогают в обнаружении и исправлении ошибок, а также в поиске данных. В передаваемых данных самые левые биты кодового слова соответствуют битам сообщения, а самые правые биты кодового слова соответствуют битам четности.
Систематический код
Любой линейный блочный код может быть систематическим кодом, пока он не будет изменен. Следовательно, неизмененный блочный код называется систематическим кодом .
Ниже приведено представление структуры кодовых слов в соответствии с их распределением.
Если сообщение не изменено, оно называется систематическим кодом. Это означает, что шифрование данных не должно изменять данные.
Сверточные коды
До сих пор в линейных кодах мы обсуждали, что систематический неизмененный код является предпочтительным. Здесь данные из общего числа n битов, если переданы, k битов являются битами сообщения и (nk) битами являются биты четности.
В процессе кодирования биты четности вычитаются из целых данных, а биты сообщения кодируются. Теперь биты четности снова добавляются, и все данные снова кодируются.
На следующем рисунке приведены примеры блоков данных и потоков данных, используемых для передачи информации.
Весь процесс, изложенный выше, утомителен и имеет недостатки. Выделение буфера является основной проблемой, когда система занята.
Этот недостаток устраняется в сверточных кодах. Где весь поток данных назначается символам, а затем передается. Поскольку данные представляют собой поток битов, для хранения не требуется буфер.
Коды Хэмминга
Свойство линейности кодового слова состоит в том, что сумма двух кодовых слов также является кодовым словом. Коды Хэмминга — это тип линейных кодов, исправляющих ошибки , которые могут обнаруживать до двухбитовых ошибок или исправлять однобитовые ошибки без обнаружения неисправленных ошибок.
При использовании кодов Хэмминга дополнительные биты четности используются для идентификации ошибки одного бита. Чтобы перейти от одного бита к другому, в данных нужно изменить несколько битов. Такое количество битов можно назвать расстоянием Хэмминга . Если четность имеет расстояние 2, может быть обнаружен однобитовый переворот. Но это не может быть исправлено. Кроме того, любые два бита не могут быть обнаружены.
Тем не менее, код Хэмминга — лучшая процедура, чем обсуждаемые ранее при обнаружении и исправлении ошибок.
Коды BCH
Коды БЧХ названы в честь изобретателей B ose, C haudari и H ocquenghem. Во время разработки кода BCH существует контроль количества символов, которые должны быть исправлены, и, следовательно, возможна множественная битовая коррекция. Коды БЧХ — это мощный метод исправления ошибок.
Для любых натуральных чисел m ≥ 3 и t <2 m-1 существует двоичный код BCH. Ниже приведены параметры такого кода.
Длина блока n = 2 м -1
Количество проверочных цифр n — k ≤ mt
Минимальное расстояние d min ≥ 2t + 1
Этот код может называться кодом BCH с коррекцией ошибок .
Циклические коды
Циклическое свойство кодовых слов заключается в том, что любой циклический сдвиг кодового слова также является кодовым словом. Циклические коды следуют этому циклическому свойству.
Для линейного кода C , если каждое кодовое слово, т. Е. C = (C1, C2, …… Cn) из C, имеет циклический сдвиг вправо компонентов, оно становится кодовым словом. Этот сдвиг вправо равен n-1 циклическим сдвигам влево. Следовательно, он инвариантен при любом сдвиге. Таким образом, линейный код C , поскольку он инвариантен при любом сдвиге, можно назвать циклическим кодом .
Циклические коды используются для исправления ошибок. Они в основном используются для исправления двойных ошибок и пакетных ошибок.
Следовательно, это несколько кодов с исправлением ошибок, которые должны быть обнаружены в приемнике. Эти коды предотвращают появление ошибок и нарушают связь. Они также предотвращают прослушивание сигнала нежелательными приемниками. Для этого существует класс методов сигнализации, которые обсуждаются в следующей главе.