Мосты переменного тока

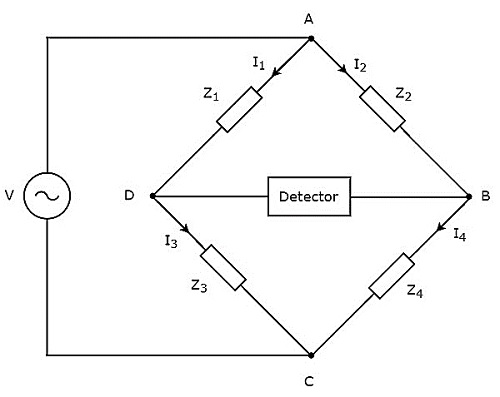
В этой главе мы поговорим о мостах переменного тока, которые можно использовать для измерения индуктивности. Мосты переменного тока работают только с сигналом переменного напряжения. Принципиальная схема моста переменного тока показана на рисунке ниже.

Как показано на рисунке выше, мост переменного тока в основном состоит из четырех плеч, которые соединены в форме ромба или квадрата . Все эти руки состоят из некоторого сопротивления.

Детектор и источник переменного напряжения также необходимы для определения значения неизвестного импеданса. Следовательно, один из этих двух размещен в одной диагонали моста переменного тока, а другой — в другой диагонали моста переменного тока. Состояние балансировки моста Уитстона как —

$$R_ {4} = \ гидроразрыва {R_ {2} R_ {3}} {R_ {1}}$$

Мы получим условие балансировки моста переменного тока , просто заменив R на Z в вышеприведенном уравнении.

$$Z_ {4} = \ гидроразрыва {Z_ {2} Z_ {3}} {Z_ {1}}$$

$\ Rightarrow Z_ {1} Z_ {4} = Z_ {2} Z_ {3}$

Здесь $Z_ {1}$ и $Z_ {2}$ являются фиксированными импедансами. Принимая во внимание, что $Z_ {3}$ является стандартным переменным сопротивлением, а $Z_ {4}$ — неизвестным сопротивлением.

Примечание. Мы можем выбрать любые два из этих четырех импедансов в качестве фиксированных импедансов, один импеданс в качестве стандартного переменного импеданса и другой импеданс в качестве неизвестного импеданса в зависимости от приложения.

Ниже приведены два моста переменного тока, которые можно использовать для измерения индуктивности .

• Максвеллов мост
• Сено мост

Теперь давайте поговорим об этих двух мостах переменного тока один за другим.

Максвеллов мост

Мост Максвелла — это мост переменного тока, имеющий четыре плеча, которые связаны в форме ромба или квадратной формы . Два плеча этого моста состоят из одного резистора, один из них состоит из последовательной комбинации резистора и индуктора, а другой — из параллельной комбинации резистора и конденсатора.

Детектор переменного тока и источник переменного напряжения используются для определения значения неизвестного импеданса. Следовательно, один из этих двух находится в одной диагонали моста Максвелла, а другой — в другой диагонали моста Максвелла.

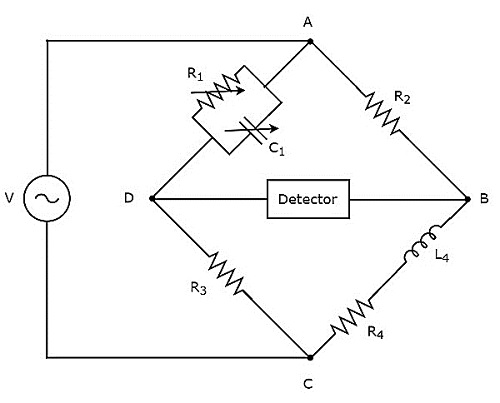
Мост Максвелла используется для измерения значения средней индуктивности. Принципиальная схема моста Максвелла показана на рисунке ниже.

В приведенной выше схеме плечи AB, BC, CD и DA вместе образуют ромб или квадратную форму. Плечи AB и CD состоят из резисторов, $R_ {2}$ и $R_ {3}$ соответственно. Плечо BC состоит из последовательной комбинации резистора $R_ {4}$ и индуктора $L_ {4}$. Плечо DA состоит из параллельной комбинации резистора $R_ {1}$ и конденсатора $C_ {1}$.

Пусть $Z_ {1}, Z_ {2}, Z_ {3}$ и $Z_ {4}$ являются импедансами плеч DA, AB, CD и BC соответственно. Значения этих сопротивлений будут

$$Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}}$$

$$\ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}$$

$Z_ {2} = R_ {2}$

$Z_ {3} = R_ {3}$

$Z_ {4} = R_ {4} + j \ omega L_ {4}$

Замените эти значения импеданса в следующем условии балансировки моста переменного тока.

$$Z_ {4} = \ гидроразрыва {Z_ {2} Z_ {3}} {Z_ {1}}$$

$$R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left ({\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} \ right)}$$

$\ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ { 1}}$

$\ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + \ frac {j \ omega R_ {1} C_ {1} R_ {2} R_ {3}} {R_ {1}}$

$\ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + j \ omega C_ {1} R_ {2} R_ {3}$

Сравнивая соответствующие вещественные и мнимые члены вышеприведенного уравнения, получим

$R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}}$ Уравнение 1

$L_ {4} = C_ {1} R_ {2} R_ {3}$ Уравнение 2

Подставляя значения резисторов $R_ {1}$, $R_ {2}$ и $R_ {3}$ в уравнение 1, мы получим значение резистора, $R_ {4}$. Аналогично, подставляя значение конденсатора, $C_ {1}$ и значения резисторов, $R_ {2}$ и $R_ {3}$ в уравнении 2, мы получим значение индуктора, $L_ {4 }$.

Преимущество моста Максвелла состоит в том, что оба значения резистора $R_ {4}$ и индуктора $L_ {4}$ не зависят от значения частоты.

Сено мост

Мост Хэя является модифицированной версией моста Максвелла, который мы получаем, модифицируя плечо, которое состоит из параллельной комбинации резистора и конденсатора в плечо, которое состоит из последовательной комбинации резистора и конденсатора в мосте Максвелла.

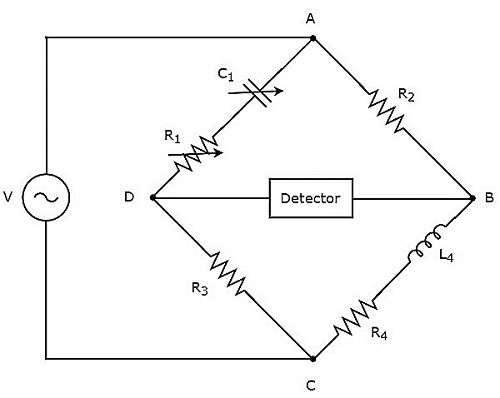
Мост Хэя используется для измерения значения высокой индуктивности. Принципиальная схема моста Хэя показана на рисунке ниже.

В приведенной выше схеме плечи AB, BC, CD и DA вместе образуют ромб или квадратную форму. Плечи, AB и CD состоят из резисторов, $R_ {2}$ и $R_ {3}$ соответственно. Плечо BC состоит из последовательной комбинации резистора $R_ {4}$ и индуктора $L_ {4}$. Плечо DA состоит из последовательной комбинации резистора $R_ {1}$ и конденсатора $C_ {1}$.

Пусть $Z_ {1}, Z_ {2}, Z_ {3}$ и $Z_ {4}$ являются импедансами плеч DA, AB, CD и BC соответственно. Значения этих сопротивлений будут

$$Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}}$$

$\ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}}$

$Z_ {2} = R_ {2}$

$Z_ {3} = R_ {3}$

$Z_ {4} = R_ {4} + j \ omega L_ {4}$

Замените эти значения импеданса в следующем условии балансировки моста переменного тока.

$$Z_ {4} = \ гидроразрыва {Z_ {2} Z_ {3}} {Z_ {1}}$$

$R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ омега C_ {1}} \ right)}$

$R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ {1} \ right)}$

Умножьте числитель и знаменатель члена правой части вышеприведенного уравнения на $1 - j \ omega R_ {1} C_ {1}$.

$\ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ { 1} \ right)} \ times \ frac {\ left (1 - j \ omega R_ {1} C_ {1} \ right)} {\ left (1 - j \ omega R_ {1} C_ {1} \ right )}$

$\ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3} + j \ omega R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)}$

Сравнивая соответствующие вещественные и мнимые члены вышеприведенного уравнения, получим

$R_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)}$ Уравнение 3

$L_ {4} = \ frac {R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)}$ Уравнение 4

Подставляя значения $R_ {1}, R_ {2}, R_ {3}, C_ {1}$ и $\ omega$ в уравнение 3 и уравнение 4, мы получим значения резистора, $R_ {4 }$ и индуктор, $L_ {4}$.