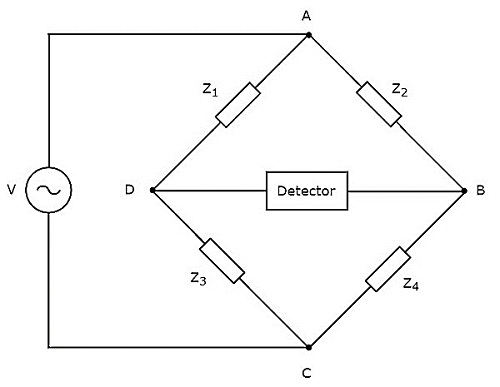
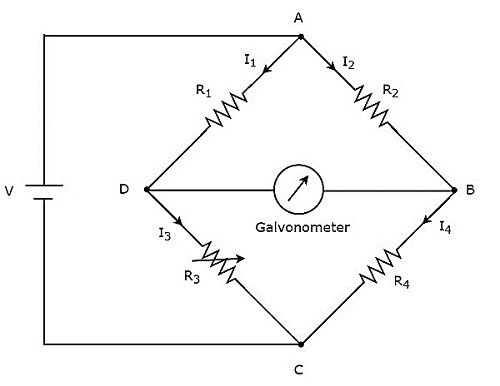
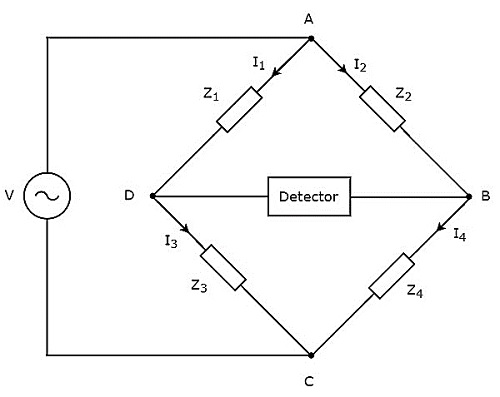
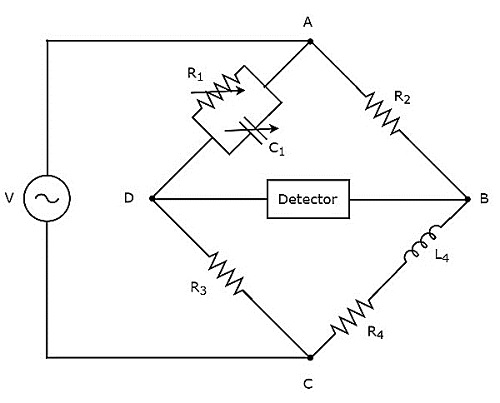
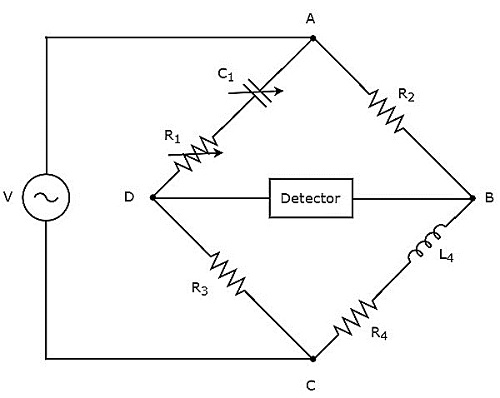
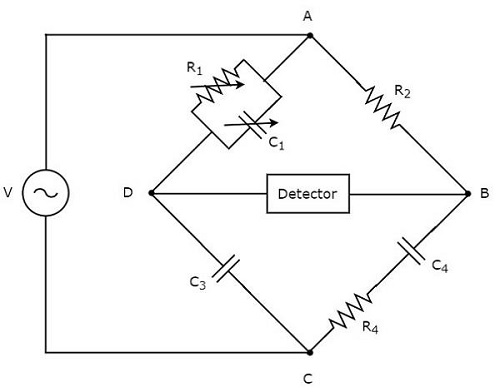
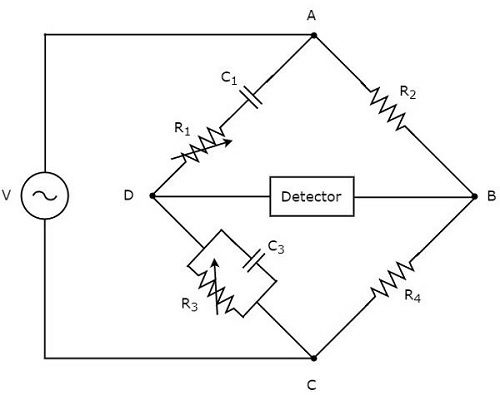
Вступление

Инструменты, которые используются для измерения любого количества, известны как измерительные инструменты. Этот учебник охватывает в основном электронные приборы , которые полезны для измерения электрических величин или параметров.

Ниже приведены наиболее часто используемые электронные инструменты.

• Вольтметр
• Амперметр
• омметр
• мультиметр

Теперь давайте кратко обсудим эти инструменты.

Вольтметр

Как следует из названия, вольтметр является измерительным прибором, который измеряет напряжение в любых двух точках электрической цепи. Существует два типа вольтметров: вольтметр постоянного тока и вольтметр переменного тока.

Вольтметр постоянного тока измеряет напряжение постоянного тока в любых двух точках электрической цепи, тогда как вольтметр переменного тока измеряет напряжение переменного тока в любых двух точках электрической цепи. Пример практического вольтметра постоянного тока показан на рисунке ниже.

Вольтметр постоянного тока, показанный на рисунке выше, представляет собой вольтметр постоянного тока $(0-100) V$ . Следовательно, его можно использовать для измерения напряжения постоянного тока от нуля до 10 вольт.

Амперметр

Как следует из названия, амперметр — это измерительный прибор, который измеряет ток, протекающий через любые две точки электрической цепи. Существует два типа амперметров: амперметр постоянного тока и амперметр переменного тока.

Амперметр постоянного тока измеряет постоянный ток, который протекает через любые две точки электрической цепи. Принимая во внимание, что амперметр переменного тока измеряет переменный ток, который течет через любые две точки электрической цепи. Пример практического амперметра переменного тока показан на рисунке ниже —

Амперметр переменного тока, показанный на рисунке выше, представляет собой амперметр переменного тока (0−100)A$(0-100) A \:$ . Следовательно, его можно использовать для измерения переменного тока от нуля до 100 ампер.

омметр

Омметр используется для измерения значения сопротивления между любыми двумя точками электрической цепи. Он также может быть использован для определения значения неизвестного резистора. Существует два типа омметров: последовательный омметр и шунтирующий омметр.

В омметре последовательного типа резистор, значение которого неизвестно и должно быть измерено, должен быть последовательно подключен к омметру. Это полезно для измерения высоких значений сопротивлений .

В омметре шунтового типа резистор, значение которого неизвестно и должно быть измерено, должен быть подключен параллельно (шунт) омметру. Это полезно для измерения низких значений сопротивлений .

Пример практического шунтирующего омметра показан на рисунке выше. Омметр, показанный на рисунке выше, является омметром $(0-100) \ Omega$ shunt . Следовательно, его можно использовать для измерения значений сопротивления от нуля до 100 Ом.

мультиметр

Мультиметр — это электронный прибор, используемый для измерения величин, таких как напряжение, ток и сопротивление, по одному. Он может использоваться для измерения постоянного и переменного напряжения, постоянного и переменного тока и сопротивлений нескольких диапазонов. Практический мультиметр показан на следующем рисунке —

Как показано на рисунке, этот мультиметр можно использовать для измерения различных высоких сопротивлений, низких сопротивлений, напряжений постоянного тока, напряжений переменного тока, постоянных токов и токов переменного тока. Различные масштабы и диапазон значений для каждой из этих величин отмечены на рисунке выше.

Инструменты, которые мы рассмотрели в этой главе, имеют обозначение типа инструментов , так как указатели этих инструментов отклоняются и указывают на определенное значение. Мы поговорим об этих электронных измерительных приборах подробнее в следующих главах.

Характеристики производительности

Характеристики измерительных приборов, которые помогают узнать производительность прибора и помочь в измерении любого количества или параметра, известны как рабочие характеристики .

Типы характеристик производительности

Рабочие характеристики инструментов можно классифицировать на следующие два типа .

• Статические характеристики
• Динамические характеристики

Теперь давайте поговорим об этих двух типах характеристик одна за другой.

Статические характеристики

Характеристики величин или параметров измерительных приборов, которые не меняются во времени, называются статическими характеристиками. Иногда эти величины или параметры могут медленно изменяться во времени. Ниже приведен список статических характеристик .

• точность
• точность
• чувствительность
• разрешение
• Статическая ошибка

Теперь давайте поговорим об этих статических характеристиках один за другим.

точность

Алгебраическая разница между указанным значением инструмента, $A_ {i}$, и истинным значением, $A_ {t}$, называется точностью . Математически это можно представить как —

$$Точность = A_ {i} - A_ {t}$$

Термин «точность» означает, насколько указанное значение инструмента, $A_ {i}$, ближе к истинному значению, $A_ {t}$.

Статическая ошибка

Разница между истинным значением, $A_ {t}$ количества, которое не изменяется во времени, и указанным значением инструмента, $A_ {i}$, называется статической ошибкой , $e_ {s}$ , Математически это можно представить как —

$$e_ {s} = A_ {t} - A_ {i}$$

Термин «статическая ошибка» означает неточность прибора. Если статическая ошибка представлена ​​в процентах, то она называется процентом статической ошибки . Математически это можно представить как —

$$\% e_ {s} = \ frac {e_ {s}} {A_ {t}} \ times 100$$

Подставим значение $e_ {s}$ в правой части приведенного выше уравнения —

$$\% e_ {s} = \ frac {A_ {t} - A_ {i}} {A_ {t}} \ times 100$$

Куда,

$\% e_ {s}$ — это процент статической ошибки.

точность

Если инструмент указывает одно и то же значение несколько раз, когда он используется для измерения одного и того же количества в одинаковых условиях для любого числа раз, то мы можем сказать, что инструмент имеет высокую точность .

чувствительность

Коэффициент изменения выходной мощности, $\ Delta A_ {out}$ инструмента для данного изменения входного значения, $\ Delta A_ {in}$, который должен быть измерен, называется чувствительностью, S. Математически это может быть представлено как —

$$S = \ frac {\ Delta A_ {out}} {\ Delta A_ {in}}$$

Термин « чувствительность» означает наименьшее изменение в измеряемом входном сигнале, которое требуется для реагирования прибора.

• Если калибровочная кривая является линейной , то чувствительность прибора будет постоянной и равна наклону калибровочной кривой.

• Если калибровочная кривая нелинейна , то чувствительность прибора не будет постоянной, и она будет изменяться по отношению к входу.

Если калибровочная кривая является линейной , то чувствительность прибора будет постоянной и равна наклону калибровочной кривой.

Если калибровочная кривая нелинейна , то чувствительность прибора не будет постоянной, и она будет изменяться по отношению к входу.

разрешение

Если выходной сигнал прибора будет изменяться только при наличии определенного приращения на входе, то этот прирост на входе называется разрешением . Это означает, что прибор способен эффективно измерять входной сигнал при наличии разрешения входного сигнала.

Динамические характеристики

Характеристики инструментов, которые используются для измерения величин или параметров, которые очень быстро меняются во времени, называются динамическими характеристиками. Ниже приведен список динамических характеристик .

• Скорость отклика
• Динамическая ошибка
• верность
• запаздывание

Теперь давайте поговорим об этих динамических характеристиках по одному.

Скорость отклика

Скорость, с которой прибор реагирует на любое изменение измеряемой величины, называется скоростью отклика . Это указывает на скорость работы инструмента.

запаздывание

Величина задержки, присутствующая в отклике прибора при изменении измеряемой величины, называется задержкой измерения. Это также просто называется лагом .

Динамическая ошибка

Разница между истинным значением, $A_ {t}$ величины, которая изменяется во времени, и указанным значением инструмента, $A_ {i}$, называется динамической ошибкой, $e_ {d}$.

верность

Степень, в которой прибор показывает изменение измеренной величины без какой-либо динамической ошибки, называется верностью

Электронные измерительные приборы — ошибки

Ошибки, которые возникают во время измерения, известны как ошибки измерения . В этой главе давайте поговорим о типах ошибок измерения.

Типы ошибок измерения

Мы можем классифицировать ошибки измерения по следующим трем типам.

• Грубые ошибки
• Случайные ошибки
• Систематические ошибки

Теперь давайте поговорим об этих трех типах ошибок измерения по одной.

Грубые ошибки

Ошибки, которые возникают из-за отсутствия опыта наблюдателя при измерении значений, называются грубыми ошибками . Значения грубых ошибок будут варьироваться от наблюдателя к наблюдателю. Иногда грубые ошибки также могут возникать из-за неправильного выбора инструмента. Мы можем минимизировать грубые ошибки, выполнив эти два шага.

• Выберите наиболее подходящий инструмент в зависимости от диапазона измеряемых значений.
• Внимательно запишите показания

Систематические ошибки

Если прибор выдает ошибку, которая имеет постоянное равномерное отклонение во время работы, это называется систематической ошибкой . Систематические ошибки возникают из-за характеристик материалов, используемых в приборе.

Типы систематических ошибок

Систематические ошибки могут быть классифицированы на следующие три типа .

• Инструментальные ошибки — ошибки этого типа возникают из-за недостатков инструментов и эффектов загрузки.

• Ошибки окружающей среды — ошибки этого типа возникают из-за изменений в окружающей среде, таких как изменение температуры, давления и т. Д.

• Наблюдательные ошибки — Этот тип ошибок возникает из-за наблюдателя при съемке показаний счетчика. Ошибки параллакса относятся к этому типу ошибок.

Инструментальные ошибки — ошибки этого типа возникают из-за недостатков инструментов и эффектов загрузки.

Ошибки окружающей среды — ошибки этого типа возникают из-за изменений в окружающей среде, таких как изменение температуры, давления и т. Д.

Наблюдательные ошибки — Этот тип ошибок возникает из-за наблюдателя при съемке показаний счетчика. Ошибки параллакса относятся к этому типу ошибок.

Случайные ошибки

Ошибки, возникающие из-за неизвестных источников во время измерения, называются случайными ошибками . Следовательно, невозможно устранить или минимизировать эти ошибки. Но если мы хотим получить более точные значения измерений без какой-либо случайной ошибки, то это возможно, выполнив следующие два шага.

• Шаг 1 — Проведите больше чтений разными наблюдателями.

• Шаг 2 — Проведите статистический анализ показаний, полученных на Шаге 1.

Шаг 1 — Проведите больше чтений разными наблюдателями.

Шаг 2 — Проведите статистический анализ показаний, полученных на Шаге 1.

Ниже приведены параметры, которые используются в статистическом анализе.

• Имею в виду
• медиана
• отклонение
• Отклонение
• Стандартное отклонение

Теперь давайте поговорим об этих статистических параметрах .

Имею в виду

Пусть $x_ {1}, x_ {2}, x_ {3}, ...., x_ {N}$ являются показаниями $N$ конкретного измерения. Среднее или среднее значение этих показаний может быть рассчитано по следующей формуле.

$$m = \ frac {x_ {1} + x_ {2} + x_ {3} + .... + x_ {N}} {N}$$

Где $m$ — это среднее или среднее значение.

Если количество показаний конкретного измерения больше, то среднее или среднее значение будет приблизительно равно истинному значению

медиана

Если число показаний конкретного измерения больше, тогда трудно рассчитать среднее или среднее значение. Здесь рассчитайте среднее значение, и оно будет приблизительно равно среднему значению.

Для вычисления медианного значения сначала мы должны расположить показания конкретного измерения в порядке возрастания . Мы можем вычислить среднее значение, используя следующую формулу, когда число показаний является нечетным числом .

$$M = x _ {\ left (\ frac {N + 1} {2} \ right)}$$

Мы можем рассчитать среднее значение, используя следующую формулу, когда число показаний является четным числом .

$$M = \ frac {x _ {\ left (N / 2 \ right)} + x_ \ left (\ left [N / 2 \ right] +1 \ right)} {2}$$

Отклонение от среднего

Разница между показаниями конкретного измерения и средним значением называется отклонением от среднего . Одним словом, это называется отклонением . Математически это можно представить как

$$D_ {I} = X_ {I} -m$$

Куда,

$d_ {i}$ — это отклонение чтения $i ^ {th}$ от среднего значения.

$x_ {i}$ — это значение чтения $i ^ {th}$.

$m$ — это среднее или среднее значение.

Стандартное отклонение

Среднеквадратичное отклонение называется стандартным отклонением . Математически это можно представить как

$$\ sigma = \ sqrt {\ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + { D_ {N}} ^ {2}} {N}}$$

Вышеприведенная формула действительна, если число показаний N больше или равно 20. Мы можем использовать следующую формулу для стандартного отклонения, когда число показаний N меньше 20.

$$\ sigma = \ sqrt {\ frac {{d_ {1}} ^ {2} + {d_ {2}} ^ {2} + {d_ {3}} ^ {2} + .... + { D_ {N}} ^ {2}} {N-1}}$$

Куда,

$\ sigma$ — стандартное отклонение

$d_ {1}, d_ {2}, d_ {3},…, d_ {N}$ — отклонения первого, второго, третьего,…, $N ^ {th}$ показаний от среднего значения соответственно.

Примечание. Если значение стандартного отклонения невелико, считывание значений измерения будет более точным.

отклонение

Квадрат стандартного отклонения называется дисперсией . Математически это можно представить как

$$V = \ Sigma ^ {2}$$

Куда,

$V$ — дисперсия

$\ sigma$ — стандартное отклонение

Средний квадрат отклонения также называется дисперсией . Математически это можно представить как

$$V = \ гидроразрыва {{D_ {1}} ^ {2} + {D_ {2}} ^ {2} + {D_ {3}} ^ {2} + .... + {D_ {N} } ^ {2}} {N}$$

Вышеприведенная формула действительна, если число показаний N больше или равно 20. Мы можем использовать следующую формулу для дисперсии, когда число показаний N меньше 20.

$$V = \ гидроразрыва {{D_ {1}} ^ {2} + {D_ {2}} ^ {2} + {D_ {3}} ^ {2} + .... + {D_ {N} } ^ {2}} {N-1}$$

Куда,

$V$ — дисперсия

$d_ {1}, d_ {2}, d_ {3},…, d_ {N}$ — отклонения первого, второго, третьего,…, $N ^ {th}$ показаний от среднего значения соответственно.

Итак, с помощью статистических параметров мы можем анализировать показания конкретного измерения. Таким образом, мы получим более точные значения измерений.

Электронные измерительные приборы

Инструменты, используемые для измерения любого количества, известны как измерительные инструменты . Если приборы могут измерять основные электрические величины, такие как напряжение и ток, они называются основными измерительными приборами .

Типы основных измерительных приборов

Мы можем классифицировать основные измерительные приборы по следующим двум типам.

• вольтметры
• амперметры

Давайте кратко обсудим эти два основных измерительных инструмента.

вольтметры

Как следует из названия, вольтметр является измерительным прибором, который измеряет напряжение в любых двух точках электрической цепи. Единицами напряжения являются вольт, а измерительным прибором — метр. Следовательно, слово «вольтметр» получается путем объединения двух слов «вольт» и «метр» .

Мы можем классифицировать вольтметры на следующие два типа в зависимости от типа напряжения, которое оно может измерить.

• Вольтметры постоянного тока
• Вольтметры переменного тока

Вольтметр постоянного тока

Как следует из названия, вольтметр постоянного тока измеряет напряжение постоянного тока в любых двух точках электрической цепи. Практический вольтметр постоянного тока показан на рисунке ниже.

Вольтметр постоянного тока, показанный на рисунке, представляет собой вольтметр постоянного тока $(0-10) V$ . Следовательно, его можно использовать для измерения напряжения постоянного тока от нуля до 10 вольт.

Вольтметр переменного тока

Как следует из названия, вольтметр переменного тока измеряет напряжение переменного тока в любых двух точках электрической цепи. Практический вольтметр переменного тока показан на рисунке ниже.

Вольтметр переменного тока, показанный на рисунке выше, представляет собой вольтметр переменного тока $(0-250) V$ . Следовательно, его можно использовать для измерения напряжения переменного тока от нуля до 250 вольт.

амперметры

Как следует из названия, амперметр — это измерительный прибор, который измеряет ток, протекающий через любые две точки электрической цепи. Единицей тока является ампера, а измерительным прибором — метр. Слово «амперметр» получается путем сочетания «ам» ампер с «метр» .

Мы можем классифицировать амперметры на следующие два типа в зависимости от типа тока, который он может измерять.

• Амперметры постоянного тока
• AC амперметры

Амперметр постоянного тока

Как следует из названия, амперметр постоянного тока измеряет постоянный ток, который протекает через любые две точки электрической цепи. Практический амперметр постоянного тока показан на рисунке.

Амперметр постоянного тока, показанный на рисунке выше, представляет собой амперметр постоянного тока стоимостью $(0-50) A$ . Следовательно, его можно использовать для измерения постоянного тока от нуля до 50 ампер.

Амперметр переменного тока

Как следует из названия, амперметр переменного тока измеряет переменный ток, который протекает через любые две точки электрической цепи. Практический амперметр переменного тока показан на рисунке ниже.

Амперметр переменного тока, показанный на рисунке выше, представляет собой амперметр переменного тока $(0-100) A$ . Следовательно, его можно использовать для измерения переменного тока от нуля до 100 ампер.

Мы обсудим различные вольтметры и амперметры в следующих нескольких главах.

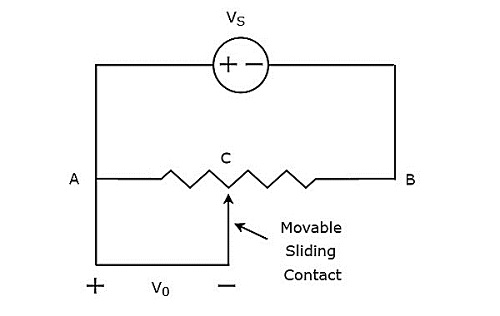
Вольтметры постоянного тока

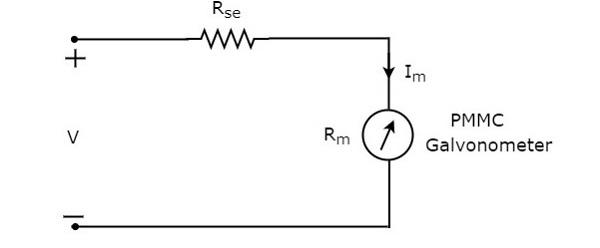
Вольтметр постоянного тока — это измерительный прибор, который используется для измерения напряжения постоянного тока в любых двух точках электрической цепи. Если мы поместим резистор последовательно с гальванометром с подвижной катушкой с постоянными магнитами (PMMC), то вся комбинация вместе будет действовать как вольтметр постоянного тока .

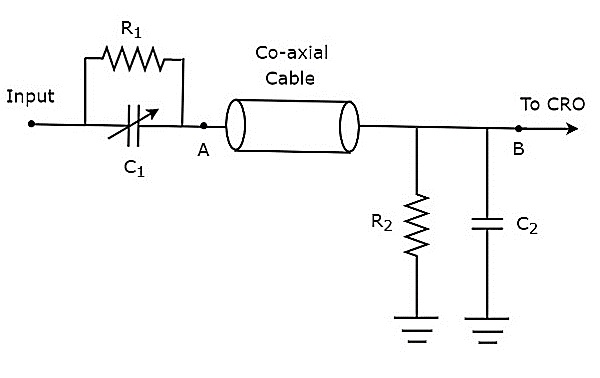
Последовательное сопротивление, которое используется в вольтметре постоянного тока, также называется последовательным множителем или просто множителем. Это в основном ограничивает количество тока, протекающего через гальванометр, чтобы предотвратить превышение током измерителя значения полной шкалы отклонения. Принципиальная схема вольтметра постоянного тока показана на рисунке ниже.

Мы должны поместить этот вольтметр постоянного тока через две точки электрической цепи, где должно измеряться напряжение постоянного тока.

Примените KVL вокруг петли вышеупомянутой цепи.

$V-I_ {m} R_ {se} -I_ {m} R_ {m} = 0$ (уравнение 1)

$$\ Rightarrow V-I_ {m} R_ {m} = I_ {m} R_ {se}$$

$$\ Rightarrow R_ {se} = \ frac {V-I_ {m} R_ {m}} {I_ {m}}$$

$\ Rightarrow R_ {se} = \ frac {V} {I_ {m}} - R_ {m}$ (уравнение 2)

Куда,

$R_ {se}$ — сопротивление множителя серии

$V$ — измеряемое постоянное напряжение полного диапазона

$I_ {m}$ — ток отклонения полной шкалы

$R_ {m}$ — внутреннее сопротивление гальванометра

Отношение измеряемого постоянного напряжения полного диапазона, $V$ и падения напряжения постоянного тока на гальванометре, $V_ {m}$, известно как множитель , м. Математически это можно представить как

$m = \ frac {V} {V_ {m}}$ (уравнение 3)

Из уравнения 1 мы получим следующее уравнение для измеряемого постоянного напряжения полного диапазона , $V$.

$V = I_ {m} R_ {se} + I_ {m} R_ {m}$ (уравнение 4)

Падение постоянного напряжения на гальванометре, $V_ {m}$, является произведением тока отклонения полной шкалы, $I_ {m}$ и внутреннего сопротивления гальванометра, $R_ {m}$. Математически это можно записать как

$V_ {m} = I_ {m} R_ {m}$ (уравнение 5)

Заменить , уравнение 4 и уравнение 5 в уравнении 3.

т= гидроразрываIтRсе+IтRтIтRм $$т = \ гидроразрыва {I_ {т} R_ {} се + I_ {т} R_ {т}} {I_ {т} R_ {м}}$$

$\ Rightarrow m = \ frac {R_ {se}} {R_ {m}} + 1$

$\ Rightarrow m-1 = \ frac {R_ {se}} {R_ {m}}$

$R_ {se} = R_ {m} \ left (m-1 \ right)$ (Уравнение 6)

Мы можем найти значение сопротивления последовательного множителя , используя либо Уравнение 2, либо Уравнение 6 на основе доступных данных.

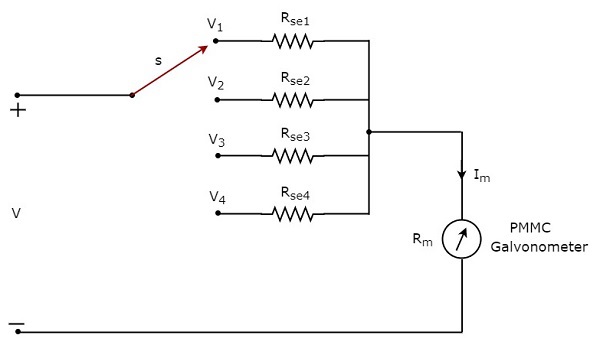
Многодиапазонный вольтметр постоянного тока

В предыдущем разделе мы обсуждали вольтметр постоянного тока, который получается путем последовательного размещения умножительного резистора с гальванометром PMMC. Этот вольтметр постоянного тока можно использовать для измерения определенного диапазона напряжений постоянного тока.

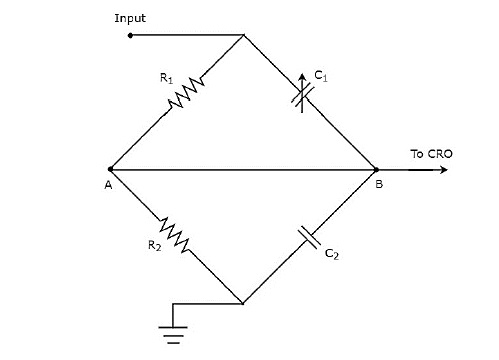
Если мы хотим использовать вольтметр постоянного тока для измерения напряжений постоянного тока в нескольких диапазонах , то вместо резистора с одним множителем мы должны использовать несколько параллельных умножительных резисторов, и вся эта комбинация резисторов включена последовательно с гальванометром PMMC. Принципиальная схема многодиапазонного вольтметра постоянного тока показана на рисунке ниже.

Мы должны поместить этот многодиапазонный вольтметр постоянного тока через две точки электрической цепи, где должно измеряться напряжение постоянного тока требуемого диапазона. Мы можем выбрать желаемый диапазон напряжений, подключив переключатель s к соответствующему резистору умножителя.

Пусть $m_ {1}, m_ {2}, m_ {2}$ и $m_ {4}$ являются множителями множителя вольтметра постоянного тока, когда мы рассматриваем измеряемые напряжения постоянного тока полного диапазона как, $V_ {1} , V_ {2}, V_ {3}$ и $V_ {4}$ соответственно. Ниже приведены формулы, соответствующие каждому множителю.

$$м_ {1} = \ {гидроразрыва V_ {1}} {V_ {м}}$$

$$м_ {2} = \ {гидроразрыва V_ {2}} {V_ {м}}$$

$$м_ {3} = \ {гидроразрыва V_ {3}} {V_ {м}}$$

$$м_ {4} = \ {гидроразрыва V_ {4}} {V_ {м}}$$

В вышеприведенной схеме есть четыре последовательных умножающих резистора , $R_ {se1}, R_ {se2}, R_ {se3}$ и $R_ {se4}$. Ниже приведены формулы, соответствующие этим четырем резисторам.

$$R_ {se1} = R_ {m} \ left (m_ {1} -1 \ right)$$

$$R_ {se2} = R_ {m} \ left (m_ {2} -1 \ right)$$

$$R_ {se3} = R_ {m} \ left (m_ {3} -1 \ right)$$

$$R_ {se4} = R_ {m} \ left (m_ {4} -1 \ right)$$

Таким образом, мы можем найти значения сопротивления каждого последовательного множительного резистора, используя приведенные выше формулы.

Вольтметры переменного тока

Прибор, который используется для измерения напряжения переменного тока в любых двух точках электрической цепи, называется вольтметром переменного тока . Если вольтметр переменного тока состоит из выпрямителя, то он называется вольтметром переменного тока на основе выпрямителя.

Вольтметр постоянного тока измеряет только напряжение постоянного тока. Если мы хотим использовать его для измерения напряжения переменного тока, мы должны выполнить следующие два шага.

• Шаг 1 — Преобразование сигнала напряжения переменного тока в сигнал напряжения постоянного тока с помощью выпрямителя.

• Шаг 2 — Измерьте постоянное или среднее значение выходного сигнала выпрямителя.

Шаг 1 — Преобразование сигнала напряжения переменного тока в сигнал напряжения постоянного тока с помощью выпрямителя.

Шаг 2 — Измерьте постоянное или среднее значение выходного сигнала выпрямителя.

Мы получаем вольтметр переменного тока на основе выпрямителя, просто включив схему выпрямителя в основной вольтметр постоянного тока. Эта глава посвящена выпрямительным вольтметрам переменного тока.

Типы вольтметров переменного тока на основе выпрямителя

Ниже приведены два типа вольтметров переменного тока на основе выпрямителя.

• Вольтметр переменного тока с использованием полуволнового выпрямителя
• Вольтметр переменного тока с использованием двухполупериодного выпрямителя

Теперь давайте поговорим об этих двух вольтметрах переменного тока один за другим.

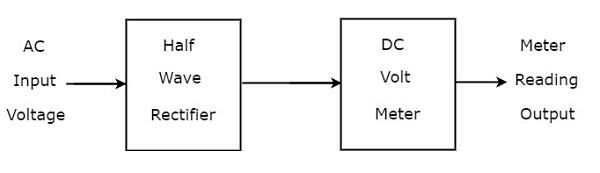
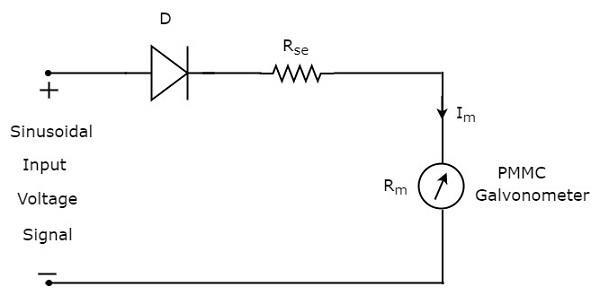
Вольтметр переменного тока с использованием полуволнового выпрямителя

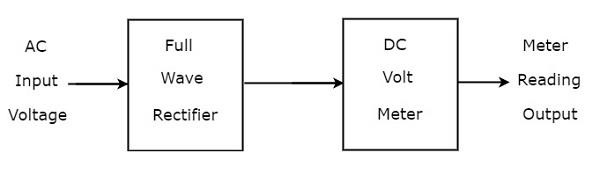
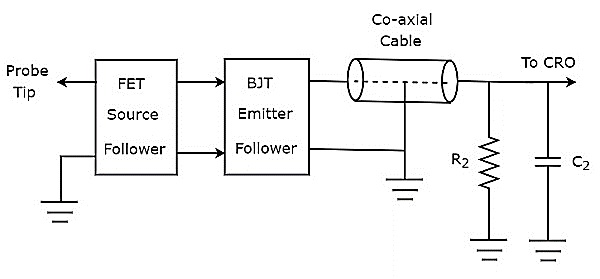
Если полуволновой выпрямитель подключен впереди вольтметра постоянного тока, то вся эта комбинация вместе называется вольтметром переменного тока с использованием полуволнового выпрямителя. Блок-схема вольтметра переменного тока с использованием полуволнового выпрямителя показана на рисунке ниже.

Приведенная блок-схема состоит из двух блоков: полуволнового выпрямителя и вольтметра постоянного тока. Мы получим соответствующую принципиальную схему, просто заменив каждый блок соответствующими компонентами на приведенной выше блок-схеме. Итак, принципиальная схема вольтметра переменного тока с использованием полуволнового выпрямителя будет выглядеть так, как показано на рисунке ниже.

Среднеквадратичное значение синусоидального (переменного) сигнала входного напряжения

$$V_ {эфф} = \ гидроразрыва {V_ {т}} {\ SQRT {2}}$$

$$\ Rightarrow V_ {m} = \ sqrt {2} V_ {rms}$$

$$\ Rightarrow V_ {m} = 1.414 V_ {rms}$$

Куда,

$V_ {m}$ — максимальное значение синусоидального (переменного) сигнала входного напряжения.

DC или среднее значение выходного сигнала полуволнового выпрямителя

Vпостоянноготока= гидроразрываVт р $$V_ {} постоянного тока = \ гидроразрыва {V_ {т}} {\ р}$$

Подставим значение $V_ {m}$ в приведенном выше уравнении.

$$V_ {dc} = \ frac {1.414 V_ {rms}} {\ pi}$$

$$V_ {dc} = 0,45 V_ {rms}$$

Следовательно, вольтметр переменного тока выдает выходное напряжение, которое в 0,45 раза превышает среднеквадратичное значение синусоидального (переменного тока) сигнала входного напряжения.

Вольтметр переменного тока с использованием двухполупериодного выпрямителя

Если двухполупериодный выпрямитель подключен впереди вольтметра постоянного тока, то вся эта комбинация вместе называется вольтметром переменного тока, использующим двухполупериодный выпрямитель. Блок-схема вольтметра переменного тока с использованием двухполупериодного выпрямителя показана на рисунке ниже.

Приведенная блок-схема состоит из двух блоков: двухполупериодного выпрямителя и вольтметра постоянного тока. Мы получим соответствующую принципиальную схему, просто заменив каждый блок соответствующими компонентами на приведенной выше блок-схеме.

Итак, принципиальная схема вольтметра переменного тока с использованием двухполупериодного выпрямителя будет выглядеть так, как показано на рисунке ниже.

Среднеквадратичное значение синусоидального (переменного) сигнала входного напряжения

$$V_ {эфф} = \ гидроразрыва {V_ {т}} {\ SQRT {2}}$$

 RightarrowVm= sqrt2Vrms $$\ Rightarrow V_ {m} = \ sqrt {2} \: V_ {rms}$$

$$\ Rightarrow V_ {m} = 1.414 V_ {rms}$$

Куда,

$V_ {m}$ — максимальное значение синусоидального (переменного) сигнала входного напряжения.

Постоянное или среднее значение выходного сигнала двухполупериодного выпрямителя

Vпостоянноготока= гидроразрыва2Vт р $$V_ {} постоянного тока = \ гидроразрыва {2V_ {т}} {\ р}$$

Подставим значение $V_ {m}$ в приведенном выше уравнении

Vdc= frac2 times1.414Vrms pi $$V_ {dc} = \ frac {2 \ times 1.414 \: V_ {rms}} {\ pi}$$

Vdc=0,9Vrms $$V_ {dc} = 0,9 \: V_ {rms}$$

Следовательно, вольтметр переменного тока выдает выходное напряжение, которое в 0,9 раза превышает среднеквадратичное значение синусоидального (переменного тока) сигнала входного напряжения.

Другие вольтметры переменного тока

В предыдущей главе мы говорили о вольтметрах переменного тока на основе выпрямителя. В этой главе рассматриваются следующие два типа вольтметров переменного тока.

• Пиковый отклик переменного вольтметра
• Истинный среднеквадратичный отклик переменного вольтметра

Теперь давайте поговорим об этих двух типах вольтметров переменного тока один за другим.

Пиковый отклик переменного вольтметра

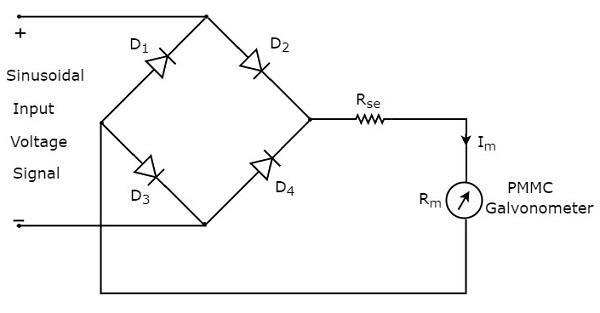
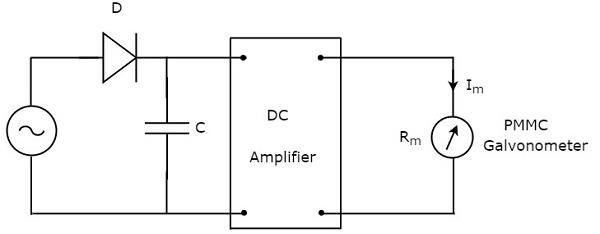
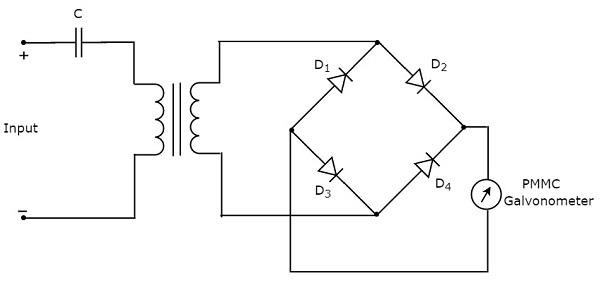
Как следует из названия, пиковый переменный вольтметр реагирует на пиковые значения сигнала переменного напряжения. Это означает, что этот вольтметр измеряет пиковые значения напряжения переменного тока. Принципиальная электрическая схема пикового вольтметра переменного тока показана ниже —

Вышеуказанная схема состоит из диода, конденсатора, усилителя постоянного тока и гальванометра PMMC. Диод, присутствующий в вышеупомянутой цепи, используется для цели выпрямления. Таким образом, диод преобразует сигнал напряжения переменного тока в сигнал напряжения постоянного тока. Конденсатор заряжается до пикового значения этого сигнала напряжения постоянного тока.

Во время положительного полупериода сигнала переменного напряжения диод проводит ток, и конденсатор заряжается до пикового значения сигнала переменного напряжения. Когда значение сигнала переменного напряжения меньше этого значения, диод будет иметь обратное смещение.

Таким образом, конденсатор разряжается через резистор усилителя постоянного тока до следующего положительного полупериода сигнала переменного напряжения. Когда значение сигнала переменного напряжения больше напряжения конденсатора, диод проводит, и процесс будет повторяться.

Мы должны выбирать значения компонентов таким образом, чтобы конденсатор быстро заряжался и разряжался медленно. В результате измеритель всегда реагирует на это напряжение конденсатора, то есть пиковое значение напряжения переменного тока .

Истинный среднеквадратичный отклик переменного вольтметра

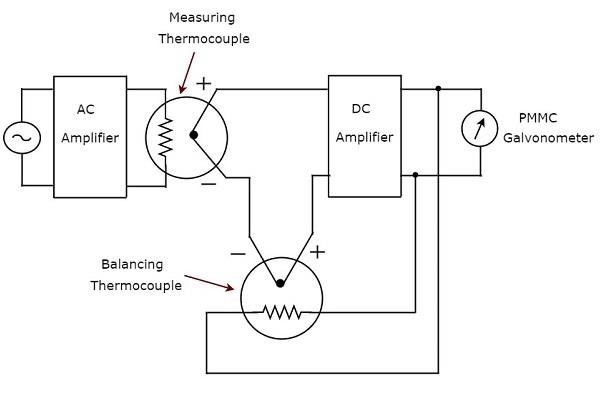
Как следует из названия, истинный среднеквадратичный отклик переменного вольтметра реагирует на истинные среднеквадратичные значения сигнала переменного напряжения. Этот вольтметр измеряет среднеквадратичные значения переменного напряжения. Принципиальная электрическая схема переменного вольтметра, реагирующего на среднеквадратичное значение, показана на рисунке ниже.

Вышеуказанная схема состоит из усилителя переменного тока, двух термопар, усилителя постоянного тока и гальванометра PMMC. Усилитель переменного тока усиливает сигнал переменного напряжения. Две термопары, которые используются в вышеупомянутой цепи, являются измерительной термопарой и балансировочной термопарой. Измерительная термопара выдает выходное напряжение, которое пропорционально среднеквадратичному значению сигнала переменного напряжения.

Любая термопара преобразует квадрат входной величины в нормальную величину. Это означает, что существует нелинейная связь между выходом и входом термопары. Эффектом нелинейного поведения термопары можно пренебречь, если использовать другую термопару в цепи обратной связи. Термопара, которая используется для этой цели в вышеупомянутой схеме, известна как уравновешивающая термопара .

Две термопары, а именно измерительная термопара и уравновешивающая термопара вместе образуют невесту на входе усилителя постоянного тока. В результате счетчик всегда реагирует на истинное среднеквадратичное значение сигнала переменного напряжения.

Амперметры постоянного тока

Ток — это скорость потока электрического заряда. Если этот электрический заряд течет только в одном направлении, то результирующий ток называется постоянным током (DC). Прибор, который используется для измерения постоянного тока, называется амперметром постоянного тока .

Если поместить резистор параллельно гальванометру с подвижной катушкой с постоянными магнитами (PMMC), то вся комбинация будет действовать как амперметр постоянного тока. Параллельное сопротивление, которое используется в амперметре постоянного тока, также называется сопротивлением шунта или просто шунтом . Значение этого сопротивления следует считать малым, чтобы измерить постоянный ток большого значения.

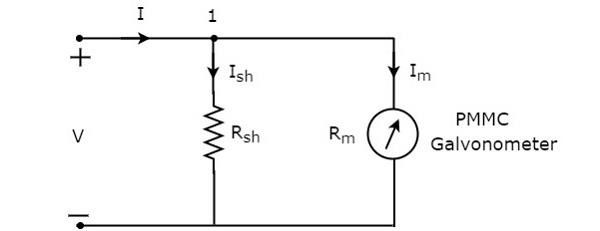
Принципиальная схема амперметра постоянного тока показана на рисунке ниже.

Мы должны поместить этот амперметр постоянного тока последовательно с ответвлением электрической цепи, где должен измеряться постоянный ток. Напряжение на элементах, которые соединены параллельно, одинаково. Таким образом, напряжение на шунтирующем резисторе, $R_ {sh}$, и напряжение на сопротивлении гальванометра, $R_ {m}$, одинаково, поскольку эти два элемента соединены параллельно в вышеуказанной цепи. Математически это можно записать как

$$I_ {ш} R_ {ш} = I_ {т} R_ {м}$$

$\ Rightarrow R_ {sh} = \ frac {I_ {m} R_ {m}} {I_ {sh}}$ (уравнение 1)

Уравнение KCL в узле 1

$$- I + I_ {ш} + I_ {т} = 0$$

$$\ Rightarrow I_ {sh} = I-I_ {m}$$

Подставьте значение $I_ {sh}$ в уравнение 1.

$R_ {sh} = \ frac {I_ {m} R_ {m}} {I-I_ {m}}$ (уравнение 2)

Возьмем $I_ {m}$ как общее в знаменателе, который присутствует в правой части уравнения 2

$$R_ {ш} = \ {гидроразрыва I_ {т} R_ {т}} {I_ {т} (\ гидроразрыва {1} {I_ {т}} - 1)}$$

$\ Rightarrow R_ {sh} = \ frac {R_ {m}} {\ frac {I} {I_ {m}} - 1}$ (уравнение 3)

Куда,

$R_ {sh}$ — сопротивление шунта

$R_ {m}$ — внутреннее сопротивление гальванометра

$I$ — общий постоянный ток, который должен быть измерен

$I_ {m}$ — ток отклонения полной шкалы

Соотношение общего постоянного тока, который должен быть измерен, $I$ и тока полной шкалы отклонения гальванометра, $I_ {m}$, известно как коэффициент умножения, м . Математически это можно представить как

$m = \ frac {I} {I_ {m}}$ (уравнение 4)

$R_ {sh} = \ frac {R_ {m}} {m-1}$ (уравнение 5)

Мы можем найти значение сопротивления шунта , используя уравнение 2 или уравнение 5 на основе доступных данных.

Многодиапазонный DC амперметр

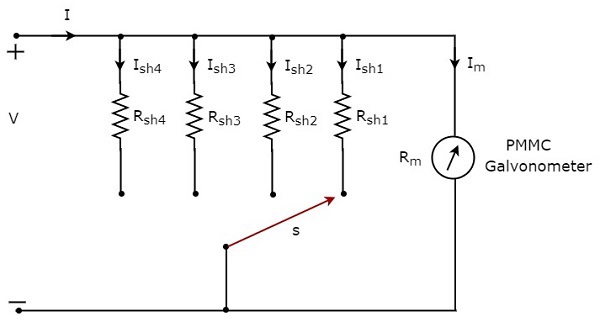
В предыдущем разделе мы обсуждали амперметр постоянного тока, который получается путем размещения резистора параллельно гальванометру PMMC. Этот амперметр постоянного тока можно использовать для измерения определенного диапазона постоянных токов.

Если мы хотим использовать амперметр постоянного тока для измерения постоянных токов в нескольких диапазонах , мы должны использовать несколько параллельных резисторов вместо одного резистора, и вся эта комбинация резисторов параллельна гальванометру PMMC. Принципиальная схема многодиапазонного амперметра постоянного тока показана на рисунке ниже.

Поместите этот многодиапазонный амперметр постоянного тока последовательно с ответвлением электрической цепи, где должен измеряться постоянный ток требуемого диапазона. Требуемый диапазон токов выбирается путем подключения переключателя s к соответствующему шунтирующему резистору.

Пусть $m_ {1}, m_ {2}, m_ {3}$ и $m_ {4}$ являются множителями множителя амперметра постоянного тока, когда мы рассматриваем суммарные постоянные токи, которые должны быть измерены как, $I_ {1}, I_ {2}, I_ {3}$ и $I_ {4}$ соответственно. Ниже приведены формулы, соответствующие каждому множителю.

$$м_ {1} = \ {гидроразрыва I_ {1}} {I_ {т}}$$

$$м_ {2} = \ {гидроразрыва I_ {2}} {I_ {т}}$$

$$м_ {3} = \ {гидроразрыва I_ {3}} {I_ {т}}$$

$$м_ {4} = \ {гидроразрыва I_ {4}} {I_ {т}}$$

В схеме выше есть четыре шунтирующих резистора , $R_ {sh1}, R_ {sh2}, R_ {sh2}$ и $R_ {sh4}$. Ниже приведены формулы, соответствующие этим четырем резисторам.

$$R_ {Ш1} = \ гидроразрыва {R_ {т}} {M_ {1} -1}$$

$$R_ {SH2} = \ гидроразрыва {R_ {т}} {M_ {2} -1}$$

$$R_ {SH3} = \ гидроразрыва {R_ {т}} {M_ {3} -1}$$

$$R_ {SH4} = \ гидроразрыва {R_ {т}} {M_ {4} -1}$$

Приведенные выше формулы помогут нам найти значения сопротивления каждого шунтирующего резистора.

Амперметр переменного тока

Ток — это скорость потока электрического заряда. Если направление этого электрического заряда регулярно меняется, то результирующий ток называется переменным током (AC) .

Прибор, который используется для измерения переменного тока, протекающего через любую ветвь электрической цепи, называется амперметром переменного тока .

Пример — Амперметр переменного тока типа термопары.

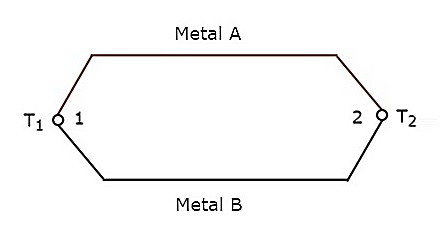
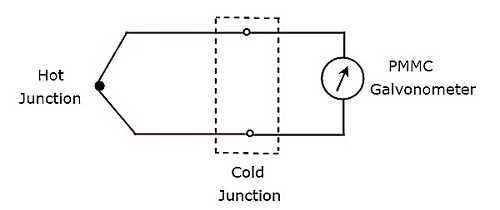
Теперь давайте обсудим амперметр переменного тока типа термопары.

Амперметр переменного тока типа термопары

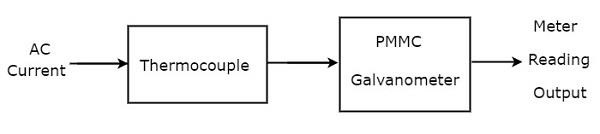
Если термопара подключена перед гальванометром PMMC, то вся эта комбинация называется амперметром переменного тока типа термопары. Блок-схема амперметра переменного тока типа термопары показана на рисунке ниже.

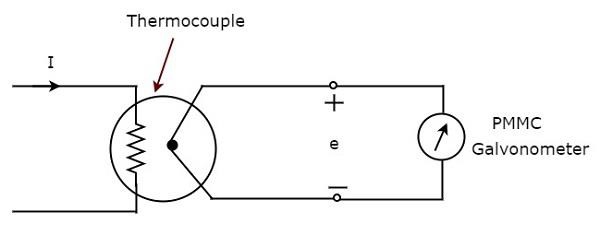
Приведенная блок-схема состоит в основном из двух блоков: термопары и гальванометра PMMC. Мы получим соответствующую принципиальную схему, просто заменив каждый блок соответствующими компонентами на приведенной выше блок-схеме. Таким образом, принципиальная схема амперметра переменного тока типа термопары будет выглядеть так, как показано на рисунке ниже.

Термопара генерирует ЭДС, $e$, всякий раз, когда переменный ток I протекает через нагревательный элемент. Эта ЭДС, $e$, прямо пропорциональна среднеквадратичному значению тока I, который протекает через нагревательный элемент. Таким образом, мы должны откалибровать шкалу прибора PMMC для считывания среднеквадратичных значений тока .

Итак, в этой главе мы завершили все основные измерительные приборы, такие как вольтметры постоянного тока, вольтметры переменного тока, амперметры постоянного тока и амперметры переменного тока. В следующей главе давайте поговорим о счетчиках или измерительных приборах, которые измеряют значение сопротивления.

Омметры

Прибор, который используется для измерения значения сопротивления между любыми двумя точками в электрической цепи, называется омметром . Его также можно использовать для определения значения неизвестного резистора. Единицами сопротивления являются ом, а измерительным прибором — метр. Таким образом, слово «омметр» получается путем сочетания слов «ом» и «метр» .

Типы омметров

Ниже приведены два типа омметров.

• Омметр серии
• Шунт Омметр

Теперь давайте поговорим об этих двух типах омметров один за другим.

Омметр серии

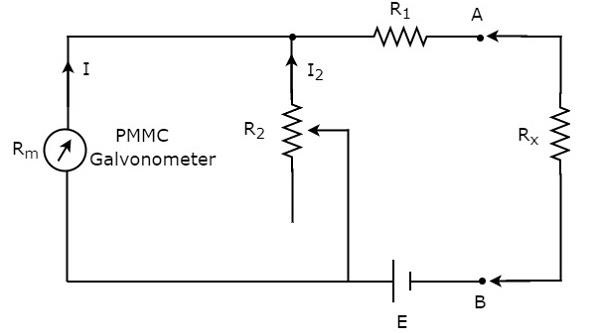
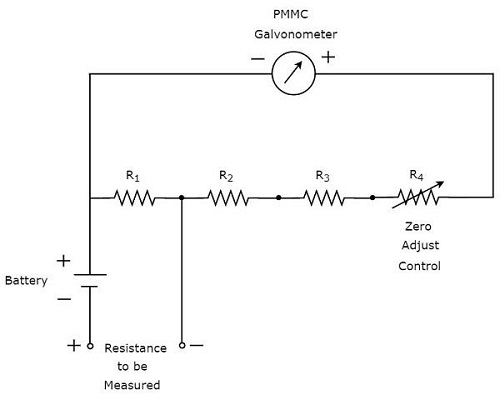
Если значение резистора неизвестно и его необходимо измерить, поместив его последовательно с омметром, то этот омметр называется последовательным омметром. Принципиальная электрическая схема омметра серии показана на рисунке ниже.

Часть цепи, которая находится слева от клемм A и B, является последовательным омметром . Итак, мы можем измерить значение неизвестного сопротивления, поместив его справа от клемм A и B. Теперь давайте поговорим о калибровочной шкале серийного омметра.

• Если $R_ {x} = 0 \: \ Omega$, то клеммы A и B будут закорочены друг с другом. Таким образом, ток счетчика делится между резисторами, $R_ {1}$ и $R_ {2}$. Теперь измените значение резистора, $R_ {2}$ таким образом, чтобы весь ток измерителя протекал через резистор, только $R_ {1}$. В этом случае счетчик показывает ток отклонения полной шкалы . Следовательно, этот полномасштабный ток отклонения измерителя может быть представлен как $0 \: \ Omega$.

• Если $R_ {x} = \ infty \: \ Omega$, то клеммы A и B будут разомкнуты друг с другом. Таким образом, через резистор ток не течет, $R_ {1}$. В этом случае счетчик показывает нулевой ток отклонения. Следовательно, это нулевое отклонение метра может быть представлено как $\ infty \ Omega$.

• Таким образом, рассматривая различные значения $R_ {x}$, измеритель показывает разные отклонения. Соответственно, мы можем представить эти отклонения с соответствующим значением сопротивления.

Если $R_ {x} = 0 \: \ Omega$, то клеммы A и B будут закорочены друг с другом. Таким образом, ток счетчика делится между резисторами, $R_ {1}$ и $R_ {2}$. Теперь измените значение резистора, $R_ {2}$ таким образом, чтобы весь ток измерителя протекал через резистор, только $R_ {1}$. В этом случае счетчик показывает ток отклонения полной шкалы . Следовательно, этот полномасштабный ток отклонения измерителя может быть представлен как $0 \: \ Omega$.

Если $R_ {x} = \ infty \: \ Omega$, то клеммы A и B будут разомкнуты друг с другом. Таким образом, через резистор ток не течет, $R_ {1}$. В этом случае счетчик показывает нулевой ток отклонения. Следовательно, это нулевое отклонение метра может быть представлено как $\ infty \ Omega$.

Таким образом, рассматривая различные значения $R_ {x}$, измеритель показывает разные отклонения. Соответственно, мы можем представить эти отклонения с соответствующим значением сопротивления.

Серийный омметр состоит из калибровочной шкалы. Он имеет обозначения 0 $\ Omega$ и $\ infty \: \ Omega$ в конечных точках правой и левой частей шкалы соответственно. Серийный омметр полезен для измерения высоких значений сопротивлений.

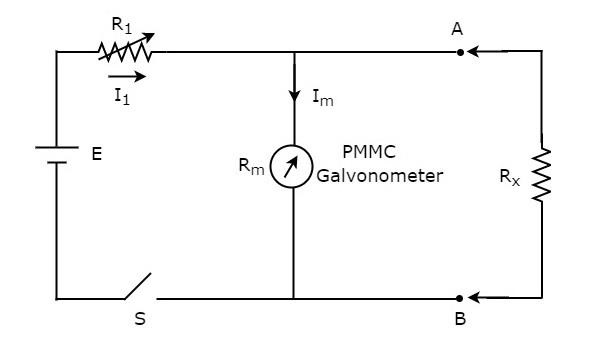
Шунт Омметр

Если значение резистора неизвестно и его необходимо измерить, поместив его параллельно (шунтирующий) с омметром, то этот омметр называется шунтирующим омметром. Принципиальная электрическая схема шунтирующего омметра показана на рисунке ниже.

Часть цепи, которая находится слева от клемм A и B, является шунтирующим омметром . Таким образом, мы можем измерить значение неизвестного сопротивления, поместив его справа от клемм A и B.

Теперь давайте поговорим о калибровочной шкале шунтирующего омметра. Замкните выключатель S вышеуказанной цепи, пока он используется.

• Если $R_ {x} = 0 \: \ Omega$, то клеммы A и B будут закорочены друг с другом. Благодаря этому весь ток $I_ {1}$ протекает через клеммы A и B. В этом случае ток не протекает через гальванометр PMMC. Следовательно, нулевое отклонение гальванометра PMMC может быть представлено как $0 \: \ Omega$.

• Если $R_ {x} = \ infty \: \ Omega$, то клеммы A и B будут разомкнуты друг с другом. Таким образом, ток не протекает через клеммы A и B. В этом случае весь ток $I_ {1}$ протекает через гальванометр PMMC. Если требуется, измените (отрегулируйте) значение резистора, $R_ {1}$, пока гальванометр PMMC не покажет ток отклонения полной шкалы. Следовательно, этот полномасштабный ток отклонения гальванометра PMMC можно представить как $\ infty \: \ Omega$

• Таким образом, рассматривая различные значения $R_ {x}$, измеритель показывает разные отклонения. Соответственно, мы можем представить эти отклонения с соответствующими значениями сопротивления.

Если $R_ {x} = 0 \: \ Omega$, то клеммы A и B будут закорочены друг с другом. Благодаря этому весь ток $I_ {1}$ протекает через клеммы A и B. В этом случае ток не протекает через гальванометр PMMC. Следовательно, нулевое отклонение гальванометра PMMC может быть представлено как $0 \: \ Omega$.

Если $R_ {x} = \ infty \: \ Omega$, то клеммы A и B будут разомкнуты друг с другом. Таким образом, ток не протекает через клеммы A и B. В этом случае весь ток $I_ {1}$ протекает через гальванометр PMMC. Если требуется, измените (отрегулируйте) значение резистора, $R_ {1}$, пока гальванометр PMMC не покажет ток отклонения полной шкалы. Следовательно, этот полномасштабный ток отклонения гальванометра PMMC можно представить как $\ infty \: \ Omega$

Таким образом, рассматривая различные значения $R_ {x}$, измеритель показывает разные отклонения. Соответственно, мы можем представить эти отклонения с соответствующими значениями сопротивления.

Шунтирующий омметр состоит из калибровочной шкалы. Он имеет обозначения $0 \: \ Omega$ и $\ infty \: \ Omega$ в конечных точках левой и правой частей шкалы соответственно.

Шунтирующий омметр полезен для измерения низких значений сопротивлений . Таким образом, мы можем использовать либо последовательный омметр, либо шунтирующий омметр, основываясь на значениях сопротивлений, которые должны быть измерены, т. Е. На высоком или на низком уровне.

MultiMeter

В предыдущих главах мы обсуждали вольтметры, амперметры и омметры. Эти измерительные приборы используются для измерения напряжения, тока и сопротивления соответственно. Это означает, что у нас есть отдельные измерительные приборы для измерения напряжения, тока и сопротивления.

Предположим, что если один измерительный прибор можно использовать для измерения величин, таких как напряжение, ток и сопротивление, по одному, то он называется мультиметром . Он получил название мультиметр, поскольку он может измерять несколько электрических величин по одному.

Измерения с использованием мультиметра

Мультиметр — это прибор, используемый для измерения постоянного и переменного напряжения, постоянного и переменного тока и сопротивлений нескольких диапазонов. Он также называется электронным мультиметром или измерителем напряжения (VOM).

Измерение постоянного напряжения

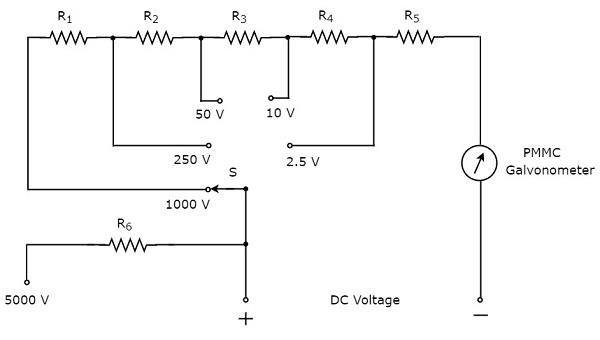
Часть принципиальной схемы мультиметра, которую можно использовать для измерения напряжения постоянного тока, показана на рисунке ниже.

Вышеуказанная схема выглядит как многодиапазонный вольтметр постоянного тока. Комбинация резистора последовательно с гальванометром PMMC представляет собой вольтметр постоянного тока . Таким образом, он может быть использован для измерения напряжения постоянного тока до определенного значения.

Мы можем увеличить диапазон напряжений постоянного тока, которые можно измерить с помощью того же вольтметра постоянного тока, увеличив значение сопротивления. эквивалентное значение сопротивления увеличивается, когда мы подключаем резисторы последовательно .

В приведенной выше схеме мы можем измерять напряжение постоянного тока до 2,5 В , используя комбинацию резисторов, $R_ {5}$ последовательно с гальванометром PMMC. Подключив резистор, $R_ {4}$ последовательно с предыдущей цепью, мы можем измерить напряжение постоянного тока до 10 В. Таким образом, мы можем увеличить диапазон напряжений постоянного тока, просто подключив резистор последовательно с предыдущей (более ранней) цепью.

Мы можем измерить напряжение постоянного тока в любых двух точках электрической цепи, подключив переключатель S к требуемому диапазону напряжения.

Измерение постоянного тока

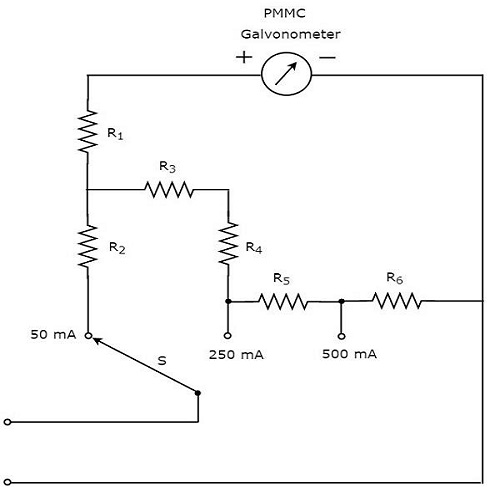
Часть принципиальной схемы мультиметра, которую можно использовать для измерения постоянного тока, показана на рисунке ниже.

Вышеуказанная схема выглядит как многодиапазонный амперметр постоянного тока. Комбинация резистора параллельно с гальванометром PMMC представляет собой амперметр постоянного тока . Таким образом, он может быть использован для измерения постоянного тока до определенного значения.

Мы можем получить различные диапазоны постоянного тока, измеренные одним и тем же амперметром постоянного тока, поместив резисторы параллельно с предыдущим резистором. В приведенной выше схеме резистор $R_ {1}$ соединен последовательно с гальванометром PMMC, чтобы предотвратить повреждение счетчика из-за большого тока.

Мы можем измерить постоянный ток, который течет через любые две точки электрической цепи, подключив переключатель S к требуемому диапазону тока

Измерение переменного напряжения

Часть принципиальной схемы мультиметра, которую можно использовать для измерения напряжения переменного тока, показана на рисунке ниже.

Вышеуказанная схема выглядит как многодиапазонный вольтметр переменного тока . Мы знаем, что мы получим вольтметр переменного тока, просто поместив выпрямитель последовательно (каскад) с вольтметром постоянного тока. Вышеуказанная схема была создана путем размещения комбинации диодов и резистора, $R_ {6}$ между резистором, $R_ {5}$ и гальванометром PMMC.

Мы можем измерить напряжение переменного тока в любых двух точках электрической цепи, подключив переключатель S к требуемому диапазону напряжения.

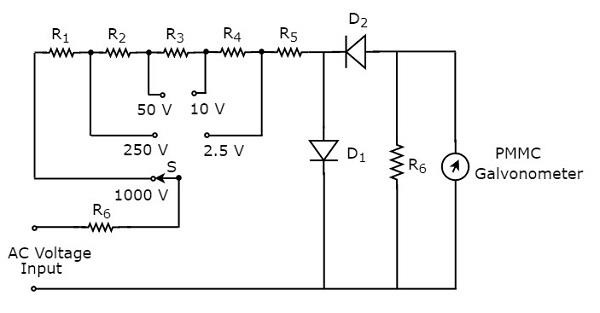
Измерение сопротивления

Часть электрической схемы мультиметра, которую можно использовать для измерения сопротивления, показана на рисунке ниже.

Мы должны выполнить следующие две задачи, прежде чем проводить какие-либо измерения.

• Короткое замыкание прибора
• Изменяйте регулировку нуля, пока измеритель не покажет ток полной шкалы. Это означает, что метр показывает нулевое значение сопротивления.

Теперь вышеприведенная схема работает как шунтирующий омметр и имеет масштабное умножение 1, то есть 10 ⁰ . Мы также можем рассматривать степени 10 высших порядков как умножения шкалы для измерения высоких сопротивлений.

Генераторы сигналов

Генератор сигналов — это электронное оборудование, которое обеспечивает стандартные тестовые сигналы, такие как синусоида, прямоугольная волна, треугольная волна и т. Д. Он также называется осциллятором, поскольку он генерирует периодические сигналы.

Генератор сигналов, который генерирует периодический сигнал, имеющий частоту диапазона звуковой частоты (AF), называется генератором сигналов AF . диапазон звуковых частот составляет от 20 Гц до 20 кГц.

AF Синусоидальный генератор

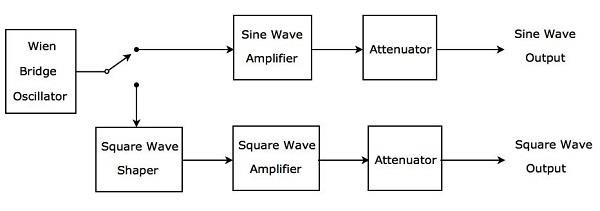
Генератор сигналов AF, который генерирует синусоидальную или прямоугольную волну в диапазоне звуковых частот в соответствии с требованиями, называется генератором синусоидальной и прямоугольной волны. Его блок-схема показана на рисунке ниже.

Приведенная блок-схема состоит в основном из двух путей . Это верхний путь и нижний путь. Верхний путь используется для создания синусоидальной волны AF, а нижний путь используется для создания прямоугольной волны AF.

Мостовой генератор Wien будет генерировать синусоидальную волну в диапазоне звуковых частот. Исходя из этого требования, мы можем подключить выход генератора Wien Bridge либо к верхнему, либо к нижнему пути с помощью переключателя.

Верхний путь состоит из блоков, таких как синусоидальный усилитель и аттенюатор. Если этот переключатель используется для подключения выхода мостового генератора Вина к верхнему тракту, он выдаст желаемую синусоидальную волну АФ на выходе верхнего тракта.

Нижний путь состоит из следующих блоков: формирователь прямоугольных импульсов, усилитель прямоугольных импульсов и аттенюатор. Формирователь прямоугольной волны преобразует синусоидальную волну в прямоугольную. Если этот переключатель используется для подключения выхода мостового генератора Вина к нижнему тракту, он будет генерировать желаемую прямоугольную волну АФ на выходе нижнего тракта. Таким образом, блок-схема, которую мы рассмотрели, может быть использована для создания синусоидальной волны AF или прямоугольной волны AF в зависимости от требований.

Генератор функций

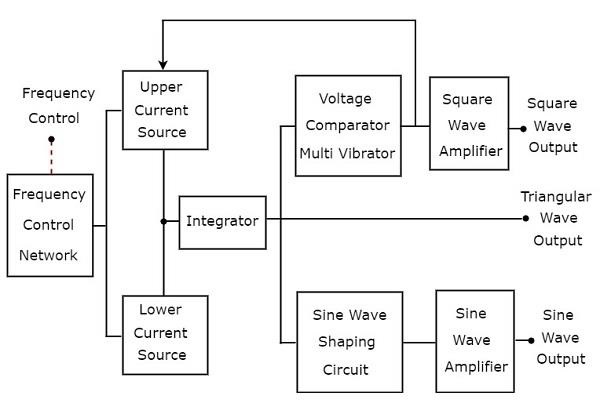
Генератор функций представляет собой генератор сигналов, который генерирует три или более периодических волн. Рассмотрим следующую блок-схему генератора функций, который будет генерировать периодические волны, такие как треугольная волна, прямоугольная волна и синусоида.

На приведенной выше блок-схеме есть два источника тока , а именно верхний источник тока и нижний источник тока. Эти два источника тока регулируются частотно-регулируемым напряжением.

Треугольная волна

Интегратор, представленный на приведенной выше блок-схеме, получает постоянный ток поочередно от верхнего и нижнего источников тока в течение одинакового промежутка времени. Таким образом, интегратор будет неоднократно производить два типа выходных данных одновременно.

• Выходное напряжение интегратора линейно увеличивается относительно времени за период, в течение которого интегратор получает ток от верхнего источника тока.

• Выходное напряжение интегратора линейно уменьшается относительно времени в течение периода, в течение которого интегратор получает ток от источника с более низким током.

Выходное напряжение интегратора линейно увеличивается относительно времени за период, в течение которого интегратор получает ток от верхнего источника тока.

Выходное напряжение интегратора линейно уменьшается относительно времени в течение периода, в течение которого интегратор получает ток от источника с более низким током.

Таким образом, интегратор, представленный на приведенной выше блок-схеме, будет генерировать треугольную волну .

Прямоугольная волна и синусоида

Выход интегратора, то есть треугольная волна, применяется в качестве входа для двух других блоков, как показано на блок-схеме выше, чтобы получить прямоугольную и синусоидальную волны соответственно. Давайте поговорим об этих двух по одному.

Прямоугольная волна

Треугольная волна имеет положительный наклон и отрицательный наклон поочередно в течение одинакового промежутка времени. Таким образом, мультивибратор компаратора напряжения, представленный на приведенной выше блок-схеме, будет генерировать следующие два типа выходных сигналов в течение одинакового промежутка времени.

• Один тип постоянного (более высокого) напряжения на выходе мультивибратора компаратора напряжения за период, в течение которого мультивибратор компаратора напряжения получает положительный наклон треугольной волны.

• Другой тип постоянного (более низкого) напряжения на выходе мультивибратора компаратора напряжения для периода, в течение которого мультивибратор компаратора напряжения получает отрицательный наклон треугольной волны.

Один тип постоянного (более высокого) напряжения на выходе мультивибратора компаратора напряжения за период, в течение которого мультивибратор компаратора напряжения получает положительный наклон треугольной волны.

Другой тип постоянного (более низкого) напряжения на выходе мультивибратора компаратора напряжения для периода, в течение которого мультивибратор компаратора напряжения получает отрицательный наклон треугольной волны.

Мультивибратор компаратора напряжения, представленный на приведенной выше блок-схеме, будет создавать прямоугольную волну . Если амплитуда прямоугольной волны, генерируемой на выходе мультивибратора компаратора напряжения, недостаточна, то ее можно усилить до требуемого значения с помощью усилителя прямоугольной волны.

Синусоидальная волна

Схема формирования синусоидальной волны будет генерировать синусоидальную волну из треугольной входной волны. По сути, эта схема состоит из сети с диодным сопротивлением. Если амплитуда синусоидальной волны, создаваемой на выходе схемы формирования синусоидальной волны, недостаточна, то ее можно усилить до требуемого значения с помощью усилителя синусоидальной волны.

Волновые анализаторы

Электронный инструмент, используемый для анализа волн, называется анализатором волн . Он также называется анализатором сигнала, поскольку термины «сигнал» и «волна» могут часто использоваться взаимозаменяемо.

Мы можем представить периодический сигнал в виде суммы следующих двух членов.

• Компонент постоянного тока
• Серия синусоидальных гармоник

Итак, анализ периодического сигнала — это анализ составляющих гармоник, представленных в нем.

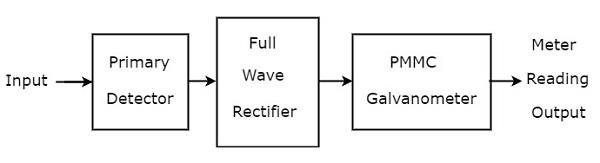
Базовый анализатор волн

Основной анализатор волн состоит в основном из трех блоков — первичного детектора, двухполупериодного выпрямителя и гальванометра PMMC. Блок-схема базового волнового анализатора показана на рисунке ниже —

Функция каждого блока, присутствующего в основном волновом анализаторе, указана ниже.

• Основной детектор — состоит из цепи LC. Мы можем отрегулировать значения индуктора L и конденсатора C таким образом, чтобы он позволял измерять только желаемую гармоническую частотную составляющую.

• Двухполупериодный выпрямитель — преобразует вход переменного тока в выход постоянного тока.

• Гальванометр PMMC — показывает пиковое значение сигнала, который получается на выходе двухполупериодного выпрямителя.

Основной детектор — состоит из цепи LC. Мы можем отрегулировать значения индуктора L и конденсатора C таким образом, чтобы он позволял измерять только желаемую гармоническую частотную составляющую.

Двухполупериодный выпрямитель — преобразует вход переменного тока в выход постоянного тока.

Гальванометр PMMC — показывает пиковое значение сигнала, который получается на выходе двухполупериодного выпрямителя.

Мы получим соответствующую принципиальную схему, просто заменив каждый блок соответствующим компонентом (-ами) в приведенной выше блок-схеме основного волнового анализатора. Итак, принципиальная схема основного волнового анализатора будет выглядеть так, как показано на следующем рисунке —

Этот базовый волновой анализатор можно использовать для анализа каждой гармонической частотной составляющей периодического сигнала.

Типы волновых анализаторов

Волновые анализаторы можно разделить на следующие два типа .

• Частотно-селективный волновой анализатор
• Супергетеродинный волновой анализатор

Теперь давайте поговорим об этих двух волновых анализаторах один за другим.

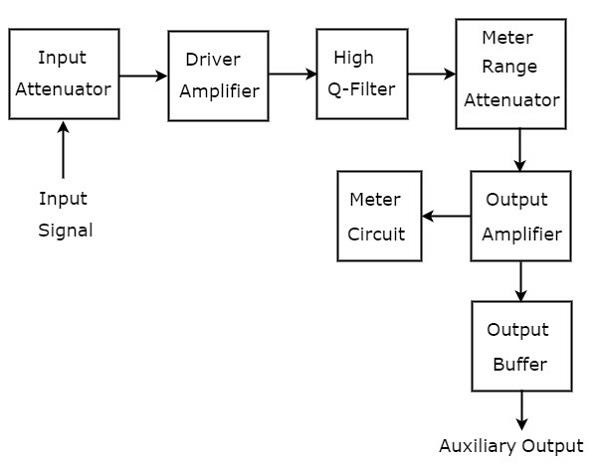
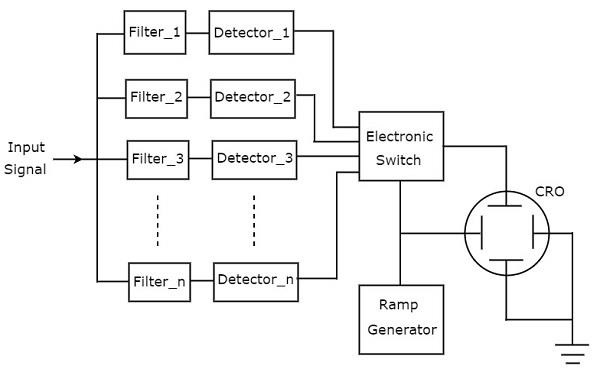
Частотно-селективный волновой анализатор

Волновой анализатор, используемый для анализа сигналов диапазона АФ, называется частотно-избирательным волновым анализатором. Блок-схема частотно-избирательного волнового анализатора показана на рисунке ниже.

Частотно-избирательный волновой анализатор состоит из набора блоков. Функция каждого блока указана ниже.

• Входной аттенюатор — Сигнал АФ, который необходимо проанализировать, подается на входной аттенюатор. Если амплитуда сигнала слишком велика, его можно ослабить с помощью входного аттенюатора.

• Driver Amplifier — усиливает полученный сигнал при необходимости.

• Высокий Q-фильтр — используется для выбора желаемой частоты и отклонения нежелательных частот. Он состоит из двух RC-секций и двух фильтрующих усилителей, и все они расположены каскадом друг с другом. Мы можем варьировать значения емкости для изменения диапазона частот в степени 10. Аналогично, мы можем варьировать значения сопротивления, чтобы изменять частоту в пределах выбранного диапазона.

• Аттенюатор измерительного диапазона — получает выбранный сигнал AF в качестве входного сигнала и создает ослабленный выходной сигнал, когда это необходимо.

• Выходной усилитель — при необходимости усиливает выбранный сигнал AF.

• Выходной буфер — используется для подачи выбранного AF-сигнала на устройства вывода.

• Meter Circuit — отображает показания выбранного сигнала AF. Мы можем выбрать показания счетчика в диапазоне вольт или децибелах.

Входной аттенюатор — Сигнал АФ, который необходимо проанализировать, подается на входной аттенюатор. Если амплитуда сигнала слишком велика, его можно ослабить с помощью входного аттенюатора.

Driver Amplifier — усиливает полученный сигнал при необходимости.

Высокий Q-фильтр — используется для выбора желаемой частоты и отклонения нежелательных частот. Он состоит из двух RC-секций и двух фильтрующих усилителей, и все они расположены каскадом друг с другом. Мы можем варьировать значения емкости для изменения диапазона частот в степени 10. Аналогично, мы можем варьировать значения сопротивления, чтобы изменять частоту в пределах выбранного диапазона.

Аттенюатор измерительного диапазона — получает выбранный сигнал AF в качестве входного сигнала и создает ослабленный выходной сигнал, когда это необходимо.

Выходной усилитель — при необходимости усиливает выбранный сигнал AF.

Выходной буфер — используется для подачи выбранного AF-сигнала на устройства вывода.

Meter Circuit — отображает показания выбранного сигнала AF. Мы можем выбрать показания счетчика в диапазоне вольт или децибелах.

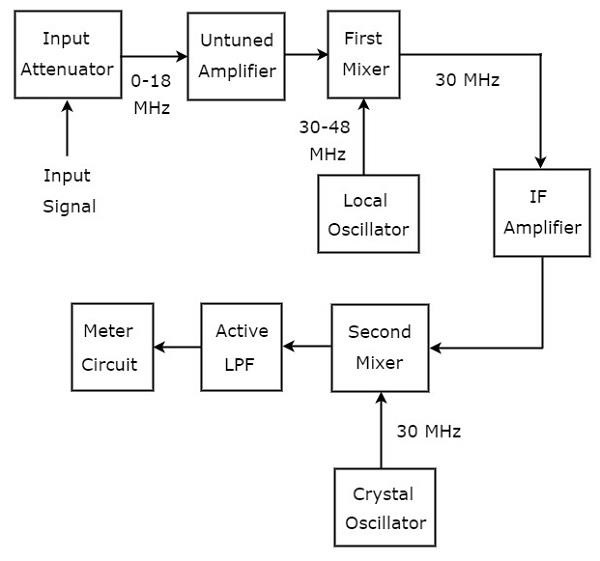
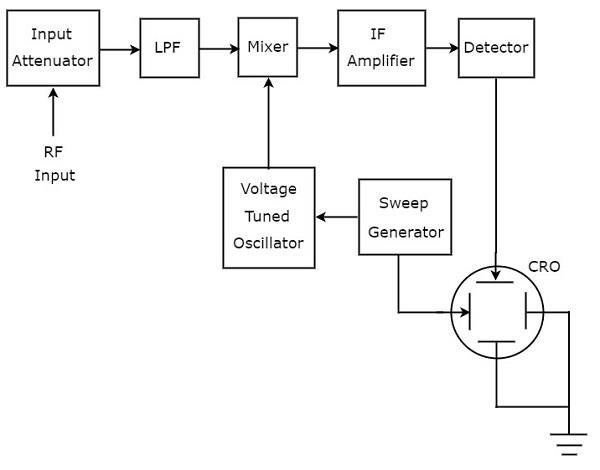
Супергетеродинный волновой анализатор

Волновой анализатор, используемый для анализа сигналов радиочастотного диапазона, называется супергетеродинным волновым анализатором. На следующем рисунке показана блок-схема супергетеродинного волнового анализатора.

Работа супергетеродинного волнового анализатора упомянута ниже.

• РЧ-сигнал, который необходимо проанализировать, подается на входной аттенюатор. Если амплитуда сигнала слишком велика, его можно ослабить с помощью входного аттенюатора .

• Ненастроенный усилитель усиливает РЧ-сигнал всякий раз, когда это необходимо, и он подается на первый микшер.

• Частотные диапазоны РЧ-сигнала и выходного сигнала гетеродина составляют 0-18 МГц и 30-48 МГц соответственно. Итак, первый микшер выдает выход с частотой 30 МГц. Это разница частот двух сигналов, которые к нему применяются.

• Усилитель ПЧ усиливает сигнал промежуточной частоты (ПЧ), т.е. выход первого микшера. Усиленный сигнал ПЧ подается на второй смеситель.

• Частоты усиленного ПЧ-сигнала и выходного сигнала кварцевого генератора одинаковы и равны 30 МГц. Итак, второй микшер выдает выходной сигнал с частотой 0 Гц. Это разница частот двух сигналов, которые к нему применяются.

• Частота среза активного фильтра нижних частот (LPF) выбрана равной 1500 Гц. Следовательно, этот фильтр разрешает выходной сигнал второго микшера.

• Meter Circuit отображает показания радиочастотного сигнала. Мы можем выбрать показания счетчика в диапазоне вольт или децибелах.

РЧ-сигнал, который необходимо проанализировать, подается на входной аттенюатор. Если амплитуда сигнала слишком велика, его можно ослабить с помощью входного аттенюатора .

Ненастроенный усилитель усиливает РЧ-сигнал всякий раз, когда это необходимо, и он подается на первый микшер.

Частотные диапазоны РЧ-сигнала и выходного сигнала гетеродина составляют 0-18 МГц и 30-48 МГц соответственно. Итак, первый микшер выдает выход с частотой 30 МГц. Это разница частот двух сигналов, которые к нему применяются.

Усилитель ПЧ усиливает сигнал промежуточной частоты (ПЧ), т.е. выход первого микшера. Усиленный сигнал ПЧ подается на второй смеситель.

Частоты усиленного ПЧ-сигнала и выходного сигнала кварцевого генератора одинаковы и равны 30 МГц. Итак, второй микшер выдает выходной сигнал с частотой 0 Гц. Это разница частот двух сигналов, которые к нему применяются.

Частота среза активного фильтра нижних частот (LPF) выбрана равной 1500 Гц. Следовательно, этот фильтр разрешает выходной сигнал второго микшера.

Meter Circuit отображает показания радиочастотного сигнала. Мы можем выбрать показания счетчика в диапазоне вольт или децибелах.

Таким образом, мы можем выбрать конкретный волновой анализатор на основе частотного диапазона анализируемого сигнала.

Анализаторы спектра

Электронный прибор, используемый для анализа волн в частотной области, называется анализатором спектра . По сути, он отображает распределение энергии сигнала на своем экране ЭЛТ. Здесь ось X представляет частоту, а ось Y представляет амплитуду.

Типы анализаторов спектра

Мы можем классифицировать анализаторы спектра по следующим двум типам .

• Фильтр Банка Спектрум Анализатор
• Супергетеродинный анализатор спектра

Теперь давайте поговорим об этих двух анализаторах спектра один за другим.

Фильтр Банка Спектрум Анализатор

Анализатор спектра, используемый для анализа сигналов диапазона АФ, называется анализатором спектра банка фильтров или анализатором спектра в реальном времени, потому что он показывает (отображает) любые изменения во всех входных частотах.

На следующем рисунке показана блок-схема анализатора спектра фильтров банка.

Работа анализатора спектра фильтров банка приведена ниже.

• Он имеет набор полосовых фильтров, и каждый из них предназначен для разрешения определенной полосы частот. Выход каждого полосового фильтра подается на соответствующий детектор.

• Все выходы детектора подключены к электронному переключателю. Этот переключатель позволяет последовательно выводить детектор на пластину вертикального отклонения CRO. Таким образом, CRO отображает частотный спектр сигнала AF на своем экране CRT.

Он имеет набор полосовых фильтров, и каждый из них предназначен для разрешения определенной полосы частот. Выход каждого полосового фильтра подается на соответствующий детектор.

Все выходы детектора подключены к электронному переключателю. Этот переключатель позволяет последовательно выводить детектор на пластину вертикального отклонения CRO. Таким образом, CRO отображает частотный спектр сигнала AF на своем экране CRT.

Супергетеродинный анализатор спектра

Анализатор спектра, используемый для анализа сигналов радиочастотного диапазона, называется супергетеродинным анализатором спектра . Его блок-схема показана на рисунке ниже.

Работа супергетеродинного спектрального анализатора упомянута ниже.

• РЧ-сигнал, который необходимо проанализировать, подается на входной аттенюатор. Если амплитуда сигнала слишком велика, он может быть ослаблен входным аттенюатором .

• Фильтр нижних частот (LPF) допускает только частотные составляющие, которые меньше частоты среза.

• Смеситель получает входные сигналы от фильтра низких частот и генератора, настроенного по напряжению. Он создает выходной сигнал, который представляет собой разницу частот двух сигналов, которые к нему применяются.

• Усилитель ПЧ усиливает сигнал промежуточной частоты (ПЧ), т. Е. Выходной сигнал микшера. Усиленный сигнал ПЧ подается на детектор.

РЧ-сигнал, который необходимо проанализировать, подается на входной аттенюатор. Если амплитуда сигнала слишком велика, он может быть ослаблен входным аттенюатором .

Фильтр нижних частот (LPF) допускает только частотные составляющие, которые меньше частоты среза.

Смеситель получает входные сигналы от фильтра низких частот и генератора, настроенного по напряжению. Он создает выходной сигнал, который представляет собой разницу частот двух сигналов, которые к нему применяются.

Усилитель ПЧ усиливает сигнал промежуточной частоты (ПЧ), т. Е. Выходной сигнал микшера. Усиленный сигнал ПЧ подается на детектор.

Выход детектора подается на вертикальную отклоняющую пластину КРО. Таким образом, CRO отображает частотный спектр РЧ-сигнала на своем экране ЭЛТ.

Таким образом, мы можем выбрать конкретный анализатор спектра на основе частотного диапазона анализируемого сигнала.

Основы осциллографов

Осциллограф — это электронное оборудование, отображающее форму волны напряжения. Среди осциллографов катодно-лучевой осциллограф (CRO) является основным и отображает изменяющийся во времени сигнал или форму волны.

В этой главе мы обсудим блок-схему CRO и измерения некоторых параметров с помощью CRO.

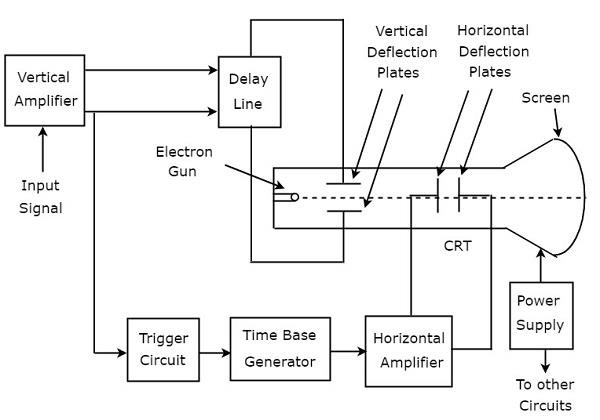
Блок-схема КРО

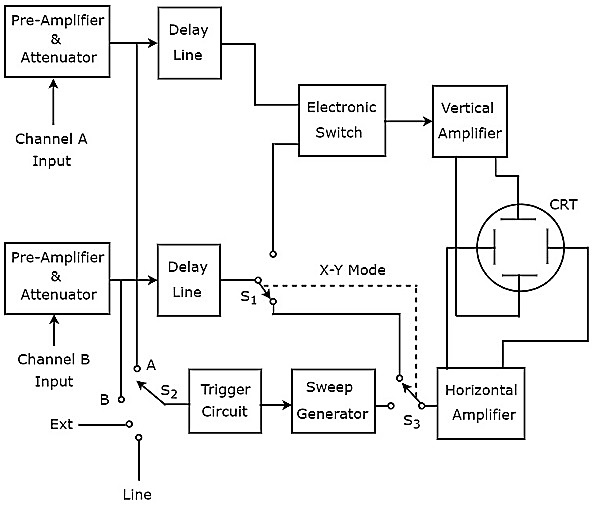
Катодно-лучевой осциллограф (CRO) состоит из набора блоков. Это вертикальный усилитель, линия задержки, схема запуска, генератор временной базы, горизонтальный усилитель, электронно-лучевая трубка (CRT) и источник питания. Блок-схема CRO показана на рисунке ниже.

Функция каждого блока CRO упоминается ниже.

• Вертикальный усилитель — усиливает входной сигнал, который должен отображаться на экране ЭЛТ.

• Линия задержки — обеспечивает некоторую задержку сигнала, получаемого на выходе вертикального усилителя. Этот задержанный сигнал затем подается на вертикальные отклоняющие пластины ЭЛТ.

• Цепь запуска — генерирует сигнал запуска для синхронизации отклонений электронного луча по горизонтали и вертикали.

• Генератор временной базы — Он генерирует пилообразный сигнал, который полезен для горизонтального отклонения электронного луча.

• Горизонтальный усилитель — усиливает пилообразный сигнал, а затем подключает его к горизонтальным отклоняющим пластинам ЭЛТ.

• Источник питания — вырабатывает как высокое, так и низкое напряжение. Отрицательное высокое напряжение и положительное низкое напряжение прикладываются к ЭЛТ и другим цепям соответственно.

• Катодно-лучевая трубка (CRT) — это важнейший блок CRO, состоящий в основном из четырех частей. Это электронная пушка, вертикальные отклоняющие пластины, горизонтальные отклоняющие пластины и флуоресцентный экран.

Вертикальный усилитель — усиливает входной сигнал, который должен отображаться на экране ЭЛТ.

Линия задержки — обеспечивает некоторую задержку сигнала, получаемого на выходе вертикального усилителя. Этот задержанный сигнал затем подается на вертикальные отклоняющие пластины ЭЛТ.

Цепь запуска — генерирует сигнал запуска для синхронизации отклонений электронного луча по горизонтали и вертикали.

Генератор временной базы — Он генерирует пилообразный сигнал, который полезен для горизонтального отклонения электронного луча.

Горизонтальный усилитель — усиливает пилообразный сигнал, а затем подключает его к горизонтальным отклоняющим пластинам ЭЛТ.

Источник питания — вырабатывает как высокое, так и низкое напряжение. Отрицательное высокое напряжение и положительное низкое напряжение прикладываются к ЭЛТ и другим цепям соответственно.

Катодно-лучевая трубка (CRT) — это важнейший блок CRO, состоящий в основном из четырех частей. Это электронная пушка, вертикальные отклоняющие пластины, горизонтальные отклоняющие пластины и флуоресцентный экран.

Электронный пучок, который создается электронной пушкой, отклоняется в вертикальном и горизонтальном направлениях с помощью пары вертикальных отклоняющих пластин и пары горизонтальных отклоняющих пластин соответственно. Наконец, отклоненный луч появится в виде пятна на флуоресцентном экране.

Таким образом, CRO будет отображать приложенный входной сигнал на экране CRT. Таким образом, мы можем анализировать сигналы во временной области с помощью CRO

Измерения с использованием CRO

Мы можем сделать следующие измерения с помощью CRO.

• Измерение амплитуды
• Измерение периода времени
• Измерение частоты

Теперь давайте поговорим об этих измерениях по одному.

Измерение амплитуды

CRO отображает сигнал напряжения как функцию времени на своем экране. Амплитуда этого сигнала напряжения постоянна, но мы можем варьировать количество делений, которые покрывают сигнал напряжения в вертикальном направлении, изменяя ручку вольт / деление на панели CRO. Поэтому мы получим амплитуду сигнала, который присутствует на экране CRO, по следующей формуле.

$$A = j \ times n_ {v}$$

Куда,

$A$ — амплитуда

$j$ — значение вольт / деление

$n_ {v}$ — количество делений, которые покрывают сигнал в вертикальном направлении.

Измерение периода времени

CRO отображает сигнал напряжения как функцию времени на своем экране. Период времени этого периодического сигнала напряжения постоянен, но мы можем варьировать количество делений, охватывающих один полный цикл сигнала напряжения в горизонтальном направлении, изменяя ручку времени / деления на панели CRO.

Следовательно, мы получим период времени сигнала, который присутствует на экране CRO, по следующей формуле.

$$T = k \ times n_ {h}$$

Куда,

$T$ — период времени

$j$ — значение времени / деления

$n_ {v}$ — это число делений, которые охватывают один полный цикл периодического сигнала в горизонтальном направлении.

Измерение частоты

Частота f периодического сигнала является обратной величиной периода времени Т. Математически она может быть представлена ​​в виде

$$F = \ гидроразрыва {1} {T},$$

Таким образом, мы можем найти частоту f периодического сигнала, выполнив следующие два шага.

• Шаг 1 — Найти период времени периодического сигнала

• Шаг 2 — Возьмите обратную величину периода времени периодического сигнала, который получается на шаге 1

Шаг 1 — Найти период времени периодического сигнала

Шаг 2 — Возьмите обратную величину периода времени периодического сигнала, который получается на шаге 1

Мы обсудим осциллографы специального назначения в следующей главе.

Осциллографы специального назначения

В предыдущей главе мы говорили о катодно-лучевом осциллографе (CRO), который является базовым осциллографом. Мы получим осциллографы специального назначения, просто включив несколько дополнительных блоков в базовый осциллограф в зависимости от требований.

Ниже приведены осциллографы специального назначения .

• Двухлучевой осциллограф
• Осциллограф Dual Trace
• Цифровой запоминающий осциллограф

Теперь давайте поговорим об этих осциллографах специального назначения один за другим.

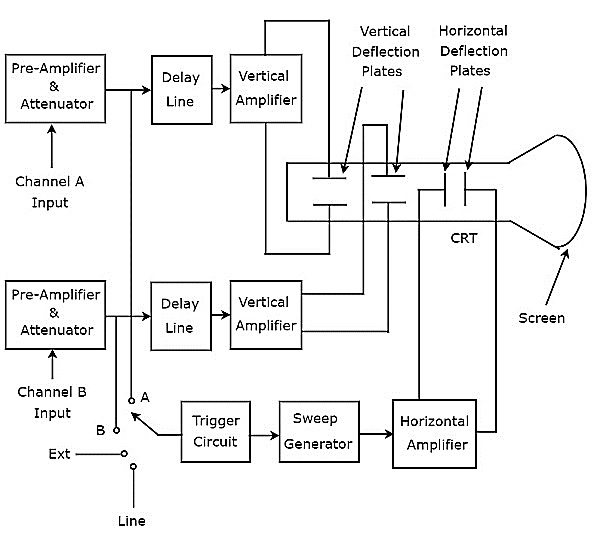
Двухлучевой осциллограф

Осциллограф, который отображает два сигнала напряжения, называется двухлучевым осциллографом. Его блок-схема показана на рисунке ниже.

Как показано на рисунке выше, ЭЛТ двухлучевого осциллографа состоит из двух наборов вертикальных отклоняющих пластин и одного набора горизонтальных отклоняющих пластин.

Комбинация следующих блоков вместе называется каналом .

• Предварительный усилитель и аттенюатор
• Линия задержки
• Вертикальный усилитель
• Набор вертикальных отклоняющих пластин

В двухлучевом осциллографе есть два канала. Таким образом, мы можем применить два сигнала, а именно A & B, как вход канала A и канала B соответственно. Мы можем выбрать любой из этих четырех сигналов в качестве входа триггера в цепь триггера, используя переключатель. Это входные сигналы A и B, внешний сигнал (Ext) и линейный вход.

Этот осциллограф будет генерировать два вертикально отклоненных луча, поскольку имеется две пары вертикальных отклоняющих пластин. В этом осциллографе блоки, которые используются для отклонения луча в горизонтальном направлении, являются общими для обоих входных сигналов. Наконец, этот осциллограф будет генерировать два входных сигнала одновременно на экране ЭЛТ.

Осциллограф Dual Trace

Осциллограф, который производит два следа на его экране, называют Двойным Осциллографом. Его блок-схема показана на рисунке ниже.

Как показано на рисунке выше, ЭЛТ осциллографа с двумя контурами состоит из набора вертикальных отклоняющих пластин и другого набора горизонтальных отклоняющих пластин. Канал состоит из четырех блоков: предварительного усилителя и аттенюатора, линии задержки, вертикального усилителя и вертикальных отклоняющих пластин.

На приведенной выше блок-схеме первые два блока отдельно присутствуют в обоих каналах. Последние два блока являются общими для обоих каналов. Следовательно, с помощью электронного переключателя мы можем подключить выход линии задержки конкретного канала к вертикальному усилителю.

Мы можем выбрать любой из этих четырех сигналов в качестве входа триггера в цепь триггера , используя переключатель. Это входные сигналы A и B, внешний сигнал (Ext) и линейный вход.

Этот осциллограф использует один и тот же электронный луч для отклонения входных сигналов A и B в вертикальном направлении с помощью электронного переключателя и производит два следа . блоки, которые отклоняют луч по горизонтали, являются общими для обоих входных сигналов.

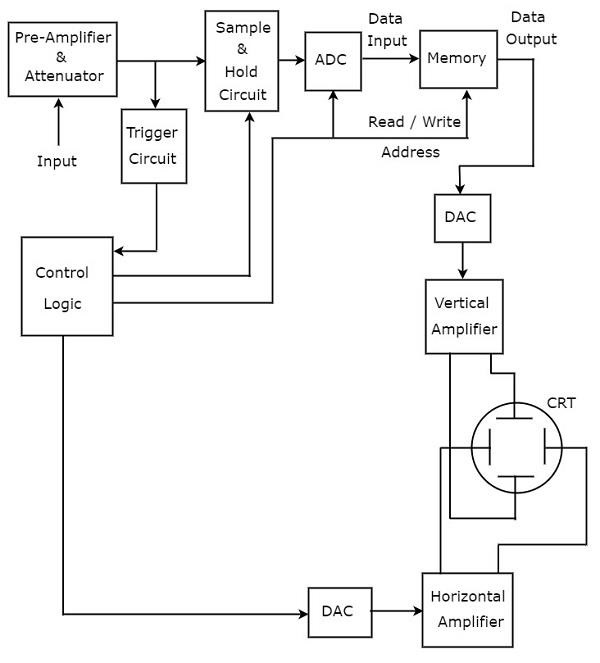
Цифровой запоминающий осциллограф

Осциллограф, который хранит форму волны в цифровой форме, известен как цифровой запоминающий осциллограф. Блок-схема (цифрового) запоминающего осциллографа ниже —

Дополнительные блоки, необходимые для хранения цифровых данных, добавляются в базовый осциллограф, чтобы преобразовать его в цифровой запоминающий осциллограф. Блоки, необходимые для хранения цифровых данных, находятся между предварительным усилителем и аттенюатором и вертикальным усилителем в цифровом запоминающем осциллографе. Это схема выборки и удержания, аналого-цифровой преобразователь (АЦП), память и цифро-аналоговый преобразователь.

Логика управления контролирует первые три блока, посылая различные сигналы управления. Такие блоки, как логика управления и цифроаналоговый преобразователь, присутствуют между схемой запуска и горизонтальным усилителем в цифровом запоминающем осциллографе.

Цифровой запоминающий осциллограф сохраняет данные в цифровом виде, прежде чем он отобразит форму сигнала на экране. Принимая во внимание, что основной осциллограф не имеет этой функции.

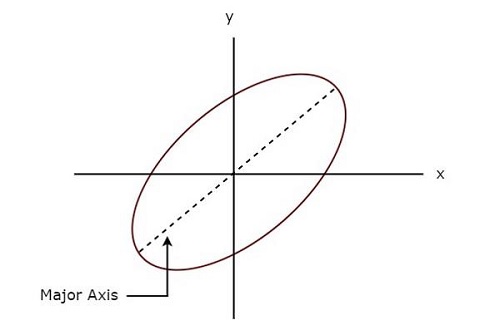
Лиссажу Фигуры

Фигура Лиссажу — это рисунок, который отображается на экране, когда синусоидальные сигналы подаются как на горизонтальные, так и на вертикальные отклоняющие пластины CRO. Эти шаблоны будут варьироваться в зависимости от амплитуд, частот и разностей фаз синусоидальных сигналов, которые применяются как к горизонтальным, так и к вертикальным отклоняющим пластинам CRO.

На следующем рисунке показан пример фигуры Лиссажу.

Вышеуказанная фигура Лиссажу имеет эллиптическую форму, а ее главная ось имеет некоторый угол наклона с положительной осью х.

Измерения с использованием фигур Лиссажу

Мы можем сделать следующие два измерения из фигуры Лиссажу.

• Частота синусоидального сигнала
• Разность фаз между двумя синусоидальными сигналами

Теперь давайте поговорим об этих двух измерениях по одному.

Измерение частоты

Фигура Лиссажу будет отображаться на экране, когда синусоидальные сигналы подаются как на горизонтальные, так и на вертикальные отклоняющие пластины CRO. Следовательно, подайте синусоидальный сигнал, который имеет стандартную известную частоту, на пластины горизонтального отклонения CRO. Аналогичным образом применяется синусоидальный сигнал, частота которого неизвестна вертикальным отклоняющим пластинам CRO

Пусть $f_ {H}$ и $f_ {V}$ — частоты синусоидальных сигналов, которые применяются к горизонтальным и вертикальным отклоняющим пластинам CRO соответственно. Соотношение между $f_ {H}$ и $f_ {V}$ можно математически представить, как показано ниже.

$$\ гидроразрыва {F_ {V}} {F_ {H}} = \ {гидроразрыва П- {H}} {П- {V}}$$

Из приведенного выше соотношения мы получим частоту синусоидального сигнала, которая применяется к пластинам вертикального отклонения CRO как

$f_ {V} = \ left (\ frac {n_ {H}} {n_ {V}} \ right) f_ {H}$ (уравнение 1)

Куда,

$n_ {H}$ — количество горизонтальных касаний

$n_ {V}$ — количество вертикальных касаний

Мы можем найти значения $n_ {H}$ и $n_ {V}$ по фигуре Лиссажу. Таким образом, подставив в уравнение 1 значения $n_ {H}$, $n_ {V}$ и $f_ {H}$, мы получим значение $f_ {V}$ , то есть частоту синусоидального сигнала. это применяется к вертикальным отклоняющим пластинам CRO.

Измерение разности фаз

Фигура Лиссажу отображается на экране, когда синусоидальные сигналы подаются как на горизонтальные, так и на вертикальные отклоняющие пластины CRO. Следовательно, применяйте синусоидальные сигналы, которые имеют одинаковую амплитуду и частоту, к горизонтальным и вертикальным отклоняющим пластинам CRO.

Для нескольких фигур Лиссажу, основанных на их форме, мы можем прямо сказать разность фаз между двумя синусоидальными сигналами.

• Если фигура Лиссажу представляет собой прямую линию с наклоном $45 ^ {\ circ}$ с положительной осью x, то разность фаз между двумя синусоидальными сигналами составит $0 ^ {\ circ}$. Это означает, что между этими двумя синусоидальными сигналами нет разности фаз.

• Если фигура Лиссажу представляет собой прямую линию с наклоном $135 ^ {\ circ}$ с положительной осью x, то разность фаз между двумя синусоидальными сигналами составит $180 ^ {\ circ}$. Это означает, что эти два синусоидальных сигнала находятся в противофазе.

• Если фигура Лиссажу имеет круглую форму , то разность фаз между двумя синусоидальными сигналами будет составлять $90 ^ {\ circ}$ или $270 ^ {\ circ}$.

Если фигура Лиссажу представляет собой прямую линию с наклоном $45 ^ {\ circ}$ с положительной осью x, то разность фаз между двумя синусоидальными сигналами составит $0 ^ {\ circ}$. Это означает, что между этими двумя синусоидальными сигналами нет разности фаз.

Если фигура Лиссажу представляет собой прямую линию с наклоном $135 ^ {\ circ}$ с положительной осью x, то разность фаз между двумя синусоидальными сигналами составит $180 ^ {\ circ}$. Это означает, что эти два синусоидальных сигнала находятся в противофазе.

Если фигура Лиссажу имеет круглую форму , то разность фаз между двумя синусоидальными сигналами будет составлять $90 ^ {\ circ}$ или $270 ^ {\ circ}$.

Мы можем рассчитать разность фаз между двумя синусоидальными сигналами, используя формулы, когда фигуры Лиссажу имеют эллиптическую форму .

• Если главная ось фигуры Лиссажу эллиптической формы, имеющая угол наклона, лежит между $0 ^ {\ circ}$ и $90 ^ {\ circ}$ с положительной осью x, то разность фаз между двумя синусоидальными сигналами будет.

Если главная ось фигуры Лиссажу эллиптической формы, имеющая угол наклона, лежит между $0 ^ {\ circ}$ и $90 ^ {\ circ}$ с положительной осью x, то разность фаз между двумя синусоидальными сигналами будет.

$$\ phi = \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = \ sin ^ {- 1} \ left (\ frac {y_ {1} } {y_ {2}} \ right)$$

• Если главная ось фигуры Лиссажу эллиптической формы, имеющая угол наклона, лежит между $90 ^ {\ circ}$ и $180 ^ {\ circ}$ с положительной осью x, то разность фаз между двумя синусоидальными сигналами будет.

Если главная ось фигуры Лиссажу эллиптической формы, имеющая угол наклона, лежит между $90 ^ {\ circ}$ и $180 ^ {\ circ}$ с положительной осью x, то разность фаз между двумя синусоидальными сигналами будет.

$$\ phi = 180 - \ sin ^ {- 1} \ left (\ frac {x_ {1}} {x_ {2}} \ right) = 180 - \ sin ^ {- 1} \ left (\ frac { y_ {1}} {y_ {2}} \ right)$$

Куда,

$x_ {1}$ — расстояние от начала координат до точки на оси х, где пересекается фигура Лиссажу эллиптической формы

$x_ {2}$ — расстояние от начала координат до вертикальной касательной эллиптической формы фигуры Лиссажу

$y_ {1}$ — расстояние от начала координат до точки на оси y, где пересекается фигура Лиссажу эллиптической формы

$y_ {2}$ — расстояние от начала координат до горизонтальной касательной эллиптической формы фигуры Лиссажу

В этой главе мы узнаем, как найти частоту неизвестного синусоидального сигнала и разность фаз между двумя синусоидальными сигналами из фигур Лиссажу, используя формулы.

CRO Probes

Мы можем подключить любую тестовую цепь к осциллографу через зонд. Поскольку CRO является базовым осциллографом, зонд, который подключен к нему, также называется CRO-зондом .

Мы должны выбрать датчик таким образом, чтобы он не создавал проблем с нагрузкой в ​​тестовой схеме. Так что мы можем правильно проанализировать тестовую схему с сигналами на экране CRO.

CRO-зонды должны иметь следующие характеристики .

• Высокий импеданс
• Высокая пропускная способность

Блок-схема датчика CRO показана на рисунке ниже.

Как показано на рисунке, CRO-зонд в основном состоит из трех блоков. Это головка зонда, коаксиальный кабель и оконечная цепь. Коаксиальный кабель просто соединяет головку зонда и концевую цепь.

Типы CRO зондов

CRO-зонды можно классифицировать на следующие два типа .

• Пассивные зонды
• Активные зонды

Теперь давайте поговорим об этих двух типах зондов один за другим.

Пассивные зонды

Если головка зонда состоит из пассивных элементов, то это называется пассивным зондом . Принципиальная схема пассивного зонда показана на рисунке ниже.

Как показано на рисунке, головка зонда состоит из параллельной комбинации резистора $R_ {1}$ и переменного конденсатора $C_ {1}$. Аналогично, оконечная цепь состоит из параллельной комбинации резистора $R_ {2}$ и конденсатора $C_ {2}$.

Вышеприведенная принципиальная схема видоизменена в виде мостовой схемы и показана на рисунке ниже.

Мы можем сбалансировать мост, отрегулировав значение переменного конденсатора, $c_ {1}$. Мы обсудим концепцию мостов в следующих главах. В настоящее время рассмотрим следующее условие балансировки моста переменного тока .

$$Z_ {1} Z_ {4} = Z_ {2} Z_ {3}$$

Замените импедансы $Z_ {1}, Z_ {2}, Z_ {3}$ и $Z_ {4}$ как $R_ {1}, \ frac {1} {j \ omega C_ {1}}, R_ {2}$ и $\ frac {1} {j \ omega C_ {2}}$ соответственно в вышеприведенном уравнении.

$$R_ {1} \ left (\ frac {1} {j \ omega C_ {2}} \ right) = \ left (\ frac {1} {j \ omega C_ {1}} \ right) R_ {2 }$$

$\ Rightarrow R_ {1} C_ {1} = R_ {2} C_ {2}$ Уравнение 1

По принципу деления напряжения мы получим напряжение на резисторе, $R_ {2}$ как

$$V_ {0} = V_ {i} \ left (\ frac {R_ {2}} {R_ {1} + R_ {2}} \ right)$$

Коэффициент ослабления — это отношение входного напряжения, $V_ {i}$ и выходного напряжения, $V_ {0}$. Итак, из вышеприведенного уравнения мы получим коэффициент затухания $\ alpha$ как

$$\ alpha = \ frac {V_ {i}} {V_ {0}} = \ frac {R_ {1} + R_ {2}} {R_ {2}}$$

$\ Rightarrow \ alpha = 1+ \ frac {R_ {1}} {R_ {2}}$

$\ Rightarrow \ alpha-1 = \ frac {R_ {1}} {R_ {2}}$

$\ Rightarrow R_ {1} = \ left (\ alpha-1 \ right) R_ {2}$ Уравнение 2

Из уравнения 2 можно сделать вывод, что значение $R_ {1}$ больше или равно значению ð ‘… 2 для целочисленных значений $\: \ alpha> 1$.

Заменить уравнение 2 на уравнение 1.

$$\ left (\ alpha-1 \ right) R_ {2} C_ {1} = R_ {2} C_ {2}$$

$\ Rightarrow \ left (\ alpha-1 \ right) C_ {1} = C_ {2}$

$\ Rightarrow C_ {1} = \ frac {C_ {2}} {\ left (\ alpha-1 \ right)}$ Уравнение 3

Из уравнения 3 можно сделать вывод, что значение $C_ {1}$ меньше или равно значению $C_ {2}$ для целочисленных значений $\ alpha> 1$.

пример

Найдем значения $R_ {1}$ и $C_ {1}$ зонда с коэффициентом затухания, $\ alpha$ равным 10. Предположим, $R_ {2} = 1 M \ Omega$ и $C_ {2} = 18pF$.

• Шаг 1 — Мы получим значение $R_ {1}$, подставив в уравнение 2 значения $\ alpha$ и $R_ {2}$.

Шаг 1 — Мы получим значение $R_ {1}$, подставив в уравнение 2 значения $\ alpha$ и $R_ {2}$.

$$R_ {1} = \ left (10-1 \ right) \ times 1 \ times 10 ^ {6}$$

$$\ Rightarrow R_ {1} = 9 \ times 10 ^ {6}$$

$$\ Rightarrow R_ {1} = 9 M \ Omega$$

Шаг 2 — Мы получим значение $C_ {1}$, подставив в уравнение 3 значения $\ alpha$ и $C_ {2}$.

$$C_ {1} = \ frac {18 \ times10 ^ {- 12}} {\ left (10-1 \ right)}$$

$$\ Rightarrow C_ {1} = 2 \ times 10 ^ {- 12}$$

$$\ Rightarrow C_ {1} = 2 пФ$$

Следовательно, значения $R_ {1}$ и $C_ {1}$ зонда будут составлять $9M \ Omega$ и $2pF$ соответственно для данных спецификаций.

Активные зонды

Если головка зонда состоит из активных электронных компонентов, то она называется активным датчиком . Блок-схема активного зонда показана на рисунке ниже.

Как показано на рисунке, головка зонда состоит из повторителя источника FET в каскаде с повторителем BJT-эмиттера. Повторитель источника FET обеспечивает высокий входной импеданс и низкий выходной импеданс. Принимая во внимание, что целью BJT-повторителя является то, что он предотвращает или устраняет рассогласование импеданса.

Две другие части, такие как коаксиальный кабель и оконечная цепь, остаются одинаковыми как в активном, так и в пассивном датчиках.

Электронные измерительные приборы — мосты

Если электрические компоненты расположены в форме моста или кольцевой структуры, то эта электрическая цепь называется мостом . В общем, мост образует петлю с набором из четырех плеч или ветвей. Каждая ветвь может содержать один или два электрических компонента.

Типы Мостов

Мы можем классифицировать мостовые схемы или мосты по следующим двум категориям на основе сигнала напряжения, с которым они могут работать.

• Мосты постоянного тока
• Мосты переменного тока

Теперь давайте кратко обсудим эти два моста.

Мосты постоянного тока

Если мостовая схема может работать только с сигналом постоянного напряжения, то это мостовая цепь постоянного тока или просто мост постоянного тока . Мосты постоянного тока используются для измерения значения неизвестного сопротивления. Принципиальная схема моста постоянного тока выглядит так, как показано на рисунке ниже.

Вышеупомянутый мост постоянного тока имеет четыре плеча, каждый из которых состоит из резистора. Среди которых два резистора имеют фиксированные значения сопротивления, один резистор является переменным резистором, а другой имеет неизвестное значение сопротивления.

Вышеупомянутая мостовая схема постоянного тока может возбуждаться источником постоянного напряжения , помещая его в одну диагональ. Гальванометр расположен в другой диагонали моста постоянного тока. Это показывает некоторое отклонение, пока мост не сбалансирован.

Изменяйте значение сопротивления переменного резистора, пока гальванометр не покажет нулевое (нулевое) отклонение. Теперь упомянутый выше мост DC считается сбалансированным. Таким образом, мы можем найти значение неизвестного сопротивления , используя узловые уравнения.

Мосты переменного тока

Если мостовая схема может работать только с сигналом переменного напряжения, то она называется мостовой цепью переменного тока или просто мостом переменного тока . Мосты переменного тока используются для измерения значения неизвестной индуктивности, емкости и частоты.

Принципиальная схема моста переменного тока выглядит так, как показано на рисунке ниже.

Принципиальная схема моста переменного тока аналогична схеме моста постоянного тока. Вышеупомянутый мост переменного тока имеет четыре плеча, и каждый рычаг состоит из некоторого импеданса. Это означает, что каждый рычаг будет иметь один или комбинацию пассивных элементов, таких как резистор, индуктор и конденсатор.

Среди четырех импедансов два импеданса имеют фиксированные значения, один импеданс является переменным, а другой — неизвестным импедансом.

Вышеупомянутая мостовая цепь переменного тока может быть возбуждена источником переменного напряжения , помещая его в одну диагональ. Детектор расположен в другой диагонали моста переменного тока. Это показывает некоторое отклонение, пока мост не сбалансирован.

Вышеупомянутая мостовая цепь переменного тока может быть возбуждена источником переменного напряжения , помещая его в одну диагональ. Детектор расположен в другой диагонали моста переменного тока. Это показывает некоторое отклонение, пока мост не сбалансирован.

Изменяйте значение импеданса переменного импеданса, пока детектор не покажет нулевое (нулевое) отклонение. Теперь вышеупомянутый мост переменного тока называется сбалансированным. Таким образом, мы можем найти значение неизвестного сопротивления , используя сбалансированное условие.

Мосты постоянного тока

Мосты постоянного тока могут работать только с сигналом постоянного напряжения. Мосты постоянного тока полезны для измерения значения неизвестного сопротивления, которое присутствует в мосте. Мост Уитстона является примером моста DC.

Теперь давайте поговорим о Мосте Уитстона, чтобы найти значение неизвестного сопротивления.

Мост Уитстона

Мост Уитстона представляет собой простой мост постоянного тока, который в основном состоит из четырех рукавов. Эти четыре плеча образуют ромб или квадратную форму, и каждый рычаг состоит из одного резистора.

Чтобы найти значение неизвестного сопротивления, нам нужны гальванометр и источник постоянного напряжения. Следовательно, один из этих двух находится в одной диагонали моста Уитстона, а другой — в другой диагонали моста Уитстона.

Мост Уитстона используется для измерения значения среднего сопротивления. Принципиальная схема моста Уитстона показана на рисунке ниже.

В приведенной выше схеме плечи AB, BC, CD и DA вместе образуют ромб или квадратную форму. Они состоят из резисторов $R_ {2}$, $R_ {4}$, $R_ {3}$ и $R_ {1}$ соответственно. Пусть ток, протекающий через эти плечи резисторов, составляет $I_ {2}$, $I_ {4}$, $I_ {3}$ и $I_ {1}$ соответственно, а направления этих токов показаны на рисунке.

Диагональные рычаги DB и AC состоят из гальванометра и источника постоянного напряжения V вольт соответственно. Здесь резистор $R_ {3}$ является стандартным переменным резистором, а резистор $R_ {4}$ — неизвестным резистором. Мы можем сбалансировать мост , изменяя значение сопротивления резистора, $R_ {3}$.

Вышеуказанная мостовая схема уравновешена, когда ток не проходит через диагональный рычаг DB. Это означает, что в гальванометре нет отклонения , когда мост сбалансирован.

Мост будет сбалансирован, когда будут выполнены следующие два условия .

• Напряжение на плече AD равно напряжению на плече AB. т.е.

Напряжение на плече AD равно напряжению на плече AB. т.е.

$$V_ {AD} = V_ {AB}$$

$\ Rightarrow I_ {1} R_ {1} = I_ {2} R_ {2}$ Уравнение 1

• Напряжение на плече постоянного тока равно напряжению на плече BC. т.е.

Напряжение на плече постоянного тока равно напряжению на плече BC. т.е.

$$V_ {DC} = V_ {BC}$$

$\ Rightarrow I_ {3} R_ {3} = I_ {4} R_ {4}$ Уравнение 2

Из приведенных выше двух условий балансировки мы получим следующие два вывода.

• Ток, протекающий через плечо AD, будет равен току плеча DC. т.е.

Ток, протекающий через плечо AD, будет равен току плеча DC. т.е.

$$I_ {1} = I_ {3}$$

• Ток, протекающий через плечо AB, будет равен току плеча BC. т.е.

Ток, протекающий через плечо AB, будет равен току плеча BC. т.е.

$$I_ {2} = I_ {4}$$

Возьмите соотношение Уравнения 1 и Уравнения 2.

$\ frac {I_ {1} R_ {1}} {I_ {3} R_ {3}} = \ frac {I_ {2} R_ {2}} {I_ {4} R_ {4}}$ Уравнение 3

Замените $I_ {1} = I_ {3}$ и $I_ {2} = I_ {4}$ в уравнении 3.

$$\ гидроразрыва {I_ {3} R_ {1}} {I_ {3} R_ {3}} = \ гидроразрыва {I_ {4} R_ {2}} {I_ {4} R_ {4}}$$

$$\ Rightarrow \ frac {R_ {1}} {R_ {3}} = \ frac {R_ {2}} {R_ {4}}$$

$$\ Rightarrow R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}}$$

Подставляя известные значения резисторов $R_ {1}$, $R_ {2}$ и $R_ {3}$ в вышеприведенное уравнение, мы получим значение резистора, $R_ {4}$ .

Мосты переменного тока

В этой главе мы поговорим о мостах переменного тока, которые можно использовать для измерения индуктивности. Мосты переменного тока работают только с сигналом переменного напряжения. Принципиальная схема моста переменного тока показана на рисунке ниже.

Как показано на рисунке выше, мост переменного тока в основном состоит из четырех плеч, которые соединены в форме ромба или квадрата . Все эти руки состоят из некоторого сопротивления.

Детектор и источник переменного напряжения также необходимы для определения значения неизвестного импеданса. Следовательно, один из этих двух размещен в одной диагонали моста переменного тока, а другой — в другой диагонали моста переменного тока. Состояние балансировки моста Уитстона как —

$$R_ {4} = \ гидроразрыва {R_ {2} R_ {3}} {R_ {1}}$$

Мы получим условие балансировки моста переменного тока , просто заменив R на Z в вышеприведенном уравнении.

$$Z_ {4} = \ гидроразрыва {Z_ {2} Z_ {3}} {Z_ {1}}$$

$\ Rightarrow Z_ {1} Z_ {4} = Z_ {2} Z_ {3}$

Здесь $Z_ {1}$ и $Z_ {2}$ являются фиксированными импедансами. Принимая во внимание, что $Z_ {3}$ является стандартным переменным сопротивлением, а $Z_ {4}$ — неизвестным сопротивлением.

Примечание. Мы можем выбрать любые два из этих четырех импедансов в качестве фиксированных импедансов, один импеданс в качестве стандартного переменного импеданса и другой импеданс в качестве неизвестного импеданса в зависимости от приложения.

Ниже приведены два моста переменного тока, которые можно использовать для измерения индуктивности .

• Максвеллов мост
• Сено мост

Теперь давайте поговорим об этих двух мостах переменного тока один за другим.

Максвеллов мост

Мост Максвелла — это мост переменного тока, имеющий четыре плеча, которые связаны в форме ромба или квадратной формы . Два плеча этого моста состоят из одного резистора, один из них состоит из последовательной комбинации резистора и индуктора, а другой — из параллельной комбинации резистора и конденсатора.

Детектор переменного тока и источник переменного напряжения используются для определения значения неизвестного импеданса. Следовательно, один из этих двух находится в одной диагонали моста Максвелла, а другой — в другой диагонали моста Максвелла.

Мост Максвелла используется для измерения значения средней индуктивности. Принципиальная схема моста Максвелла показана на рисунке ниже.

В приведенной выше схеме плечи AB, BC, CD и DA вместе образуют ромб или квадратную форму. Плечи AB и CD состоят из резисторов, $R_ {2}$ и $R_ {3}$ соответственно. Плечо BC состоит из последовательной комбинации резистора $R_ {4}$ и индуктора $L_ {4}$. Плечо DA состоит из параллельной комбинации резистора $R_ {1}$ и конденсатора $C_ {1}$.

Пусть $Z_ {1}, Z_ {2}, Z_ {3}$ и $Z_ {4}$ являются импедансами плеч DA, AB, CD и BC соответственно. Значения этих сопротивлений будут

$$Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}}$$

$$\ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}$$

$Z_ {2} = R_ {2}$

$Z_ {3} = R_ {3}$

$Z_ {4} = R_ {4} + j \ omega L_ {4}$

Замените эти значения импеданса в следующем условии балансировки моста переменного тока.

$$Z_ {4} = \ гидроразрыва {Z_ {2} Z_ {3}} {Z_ {1}}$$

$$R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left ({\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} \ right)}$$

$\ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ { 1}}$

$\ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + \ frac {j \ omega R_ {1} C_ {1} R_ {2} R_ {3}} {R_ {1}}$

$\ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + j \ omega C_ {1} R_ {2} R_ {3}$

Сравнивая соответствующие вещественные и мнимые члены вышеприведенного уравнения, получим

$R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}}$ Уравнение 1

$L_ {4} = C_ {1} R_ {2} R_ {3}$ Уравнение 2

Подставляя значения резисторов $R_ {1}$, $R_ {2}$ и $R_ {3}$ в уравнение 1, мы получим значение резистора, $R_ {4}$. Аналогично, подставляя значение конденсатора, $C_ {1}$ и значения резисторов, $R_ {2}$ и $R_ {3}$ в уравнении 2, мы получим значение индуктора, $L_ {4 }$.

Преимущество моста Максвелла состоит в том, что оба значения резистора $R_ {4}$ и индуктора $L_ {4}$ не зависят от значения частоты.

Сено мост

Мост Хэя является модифицированной версией моста Максвелла, который мы получаем, модифицируя плечо, которое состоит из параллельной комбинации резистора и конденсатора в плечо, которое состоит из последовательной комбинации резистора и конденсатора в мосте Максвелла.

Мост Хэя используется для измерения значения высокой индуктивности. Принципиальная схема моста Хэя показана на рисунке ниже.

В приведенной выше схеме плечи AB, BC, CD и DA вместе образуют ромб или квадратную форму. Плечи, AB и CD состоят из резисторов, $R_ {2}$ и $R_ {3}$ соответственно. Плечо BC состоит из последовательной комбинации резистора $R_ {4}$ и индуктора $L_ {4}$. Плечо DA состоит из последовательной комбинации резистора $R_ {1}$ и конденсатора $C_ {1}$.

Пусть $Z_ {1}, Z_ {2}, Z_ {3}$ и $Z_ {4}$ являются импедансами плеч DA, AB, CD и BC соответственно. Значения этих сопротивлений будут

$$Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}}$$

$\ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}}$

$Z_ {2} = R_ {2}$

$Z_ {3} = R_ {3}$

$Z_ {4} = R_ {4} + j \ omega L_ {4}$

Замените эти значения импеданса в следующем условии балансировки моста переменного тока.

$$Z_ {4} = \ гидроразрыва {Z_ {2} Z_ {3}} {Z_ {1}}$$

$R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ омега C_ {1}} \ right)}$

$R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ {1} \ right)}$

Умножьте числитель и знаменатель члена правой части вышеприведенного уравнения на $1 - j \ omega R_ {1} C_ {1}$.

$\ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ { 1} \ right)} \ times \ frac {\ left (1 - j \ omega R_ {1} C_ {1} \ right)} {\ left (1 - j \ omega R_ {1} C_ {1} \ right )}$

$\ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3} + j \ omega R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)}$

Сравнивая соответствующие вещественные и мнимые члены вышеприведенного уравнения, получим

$R_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)}$ Уравнение 3

$L_ {4} = \ frac {R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)}$ Уравнение 4

Подставляя значения $R_ {1}, R_ {2}, R_ {3}, C_ {1}$ и $\ omega$ в уравнение 3 и уравнение 4, мы получим значения резистора, $R_ {4 }$ и индуктор, $L_ {4}$.

Другие мосты переменного тока

В предыдущей главе мы обсудили два моста переменного тока, которые можно использовать для измерения индуктивности. В этой главе давайте поговорим о следующих двух мостах переменного тока .

• Мост Шеринг
• Мост Вены

Эти два моста могут быть использованы для измерения емкости и частоты соответственно.

Мост Шеринг

Мост Шеринга представляет собой мост переменного тока, имеющий четыре плеча, которые соединены в форме ромба или квадратной формы , одно плечо которого состоит из одного резистора, одно плечо состоит из последовательной комбинации резистора и конденсатора, одно плечо состоит из одного Конденсатор и другое плечо состоят из параллельной комбинации резистора и конденсатора.

Детектор переменного тока и источник переменного напряжения также используются для определения значения неизвестного импеданса, поэтому один из них расположен на одной диагонали моста Шеринга, а другой — на другой диагонали моста Шеринга.

Шеринг-мост используется для измерения значения емкости. Принципиальная схема моста Шеринга показана на рисунке ниже.

В приведенной выше схеме плечи AB, BC, CD и DA вместе образуют ромб или квадратную форму . Плечо AB состоит из резистора, $R_ {2}$. Плечо BC состоит из последовательной комбинации резистора $R_ {4}$ и конденсатора $C_ {4}$. Диск CD состоит из конденсатора $C_ {3}$. Плечо DA состоит из параллельной комбинации резистора $R_ {1}$ и конденсатора $C_ {1}$.

Пусть $Z_ {1}$, $Z_ {2}$, $Z_ {3}$ и $Z_ {4}$ являются импедансами плеч DA, AB, CD и BC соответственно. Значения этих сопротивлений будут

$Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}}$

$\ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}$

$Z_ {2} = R_ {2}$

$Z_ {3} = \ frac {1} {j \ omega C_ {3}}$

$Z_ {4} = R_ {4} + \ frac {1} {j \ omega C_ {4}}$

$\ Rightarrow Z_ {4} = \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}}$

Замените эти значения импеданса в следующем условии балансировки моста переменного тока.

$$Z_ {4} = \ гидроразрыва {Z_ {2} Z_ {3}} {Z_ {1}}$$

$$\ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (\ frac {1} {j \ omega C_ { 3}} \ right)} {\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}}$$

$\ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {j \ omega R_ {1} C_ {3}}$

$\ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ {1} C_ {3}}$

$\ Rightarrow \ frac {1} {C_ {4}} + j \ omega R_ {4} = \ frac {R_ {2}} {R_ {1} C_ {3}} + \ frac {j \ omega C_ { 1} R_ {2}} {C_ {3}}$

Сравнивая соответствующие вещественные и мнимые члены вышеприведенного уравнения, получим

$C_ {4} = \ frac {R_ {1} C_ {3}} {R_ {2}}$ Уравнение 1

$R_ {4} = \ frac {C_ {1} R_ {2}} {C_ {3}}$ Уравнение 2

Подставляя значения $R_ {1}, R_ {2}$ и $C_ {3}$ в уравнение 1, мы получим значение конденсатора, $C_ {4}$. Аналогично, подставляя значения уравнения $R_ {2}, C_ {1}$ и $C_ {3}$ в уравнение 2, мы получим значение резистора, $R_ {4}$.

Преимущество моста Шеринга состоит в том, что оба значения резистора, $R_ {4}$ и конденсатора, $C_ {4}$, не зависят от значения частоты.

Мост Вены

Мост Вена — это мост переменного тока, имеющий четыре плеча, которые связаны в форме ромба или квадратной формы. Среди двух плеч состоит из одного резистора, один плечо состоит из параллельной комбинации резистора и конденсатора, а другой плечо состоит из последовательной комбинации резистора и конденсатора.

Детектор переменного тока и источник переменного напряжения также необходимы для того, чтобы найти значение частоты. Следовательно, один из этих двух находится в одной диагонали моста Вена, а другой — в другой диагонали моста Вена.

Принципиальная схема моста Вена показана на рисунке ниже.

В приведенной выше схеме плечи AB, BC, CD и DA вместе образуют ромб или квадратную форму . Плечи, AB и BC состоят из резисторов, $R_ {2}$ и $R_ {4}$ соответственно. Плечо CD состоит из параллельной комбинации резистора $R_ {3}$ и конденсатора $C_ {3}$. Плечо DA состоит из последовательной комбинации резистора $R_ {1}$ и конденсатора $C_ {1}$.

Пусть $Z_ {1}, Z_ {2}, Z_ {3}$ и $Z_ {4}$ являются импедансами плеч DA, AB, CD и BC соответственно. Значения этих сопротивлений будут

$$Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}}$$

$$\ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}}$$

$Z_ {2} = R_ {2}$

$$Z_ {3} = \ frac {R_ {3} \ left (\ frac {1} {j \ omega C_ {3}} \ right)} {R_ {3} + \ frac {1} {j \ omega C_ {3}}}$$

$$\ Rightarrow Z_ {3} = \ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}}$$

$Z_ {4} = R_ {4}$

Замените эти значения импеданса в следующем условии балансировки моста переменного тока.

$$Z_ {1} Z_ {4} = Z_ {2} Z_ {3}$$

$$\ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} \ right) R_ {4} = R_ {2} \ left (\ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} \ right)$$

$\ Rightarrow \ left (1 + j \ omega R_ {1} C_ {1} \ right) \ left (1 + j \ omega R_ {3} C_ {3} \ right) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3}$

$\ Rightarrow \ left (1 + j \ omega R_ {3} C_ {3} + j \ omega R_ {1} C_ {1} - \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3}$

$\ Rightarrow R_ {4} \ left (\ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) + j \ omega R_ {4} \ left (R_ {3} C_ {3} + R_ {1} C_ {1} \ right) = j \ omega C_ {1} R_ {2} R_ {3}$

Приравнять соответствующие реальные члены вышеприведенного уравнения.

$$R_ {4} \ left (1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) = 0$$

$\ Rightarrow 1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} = 0$

$\ Rightarrow 1 = \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3}$

$\ omega = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}}$

Замените $\ omega = 2 \ pi f$ в вышеприведенном уравнении.

$$\ Rightarrow 2 \ pi f = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}}$$

$\ Rightarrow f = \ frac {1} {2 \ pi \ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}}$

Мы можем найти значение частоты, $f$ источника переменного напряжения, подставив в вышеприведенное уравнение значения $R_ {1}, R_ {3}, C_ {1}$ и $C_ {3}$.

Если $R_ {1} = R_ {3} = R$ и $C_ {1} = C_ {3} = C$, то мы можем найти значение частоты, $f$ источника переменного напряжения, используя следующую формулу ,

$$f = \ frac {1} {2 \ pi RC}$$

Мост Вейна в основном используется для определения значения частоты диапазона АФ.

преобразователи

По сути, преобразователь преобразует одну форму энергии в другую форму энергии. Преобразователь, который преобразует неэлектрическую форму энергии в электрическую форму, известен как электрический преобразователь . Блок-схема электрического преобразователя показана на рисунке ниже.

Как показано на рисунке, электрический преобразователь будет производить выход, который имеет электрическую энергию. Выход электрического преобразователя эквивалентен входу, который имеет неэлектрическую энергию.

Типы электрических преобразователей

Преимущественно, электрические преобразователи можно классифицировать на следующие два типа .

• Активные преобразователи
• Пассивные преобразователи

Теперь давайте кратко обсудим эти два типа преобразователей.

Активные преобразователи

Преобразователь, который может генерировать одну из электрических величин, таких как напряжение и ток, известен как активный преобразователь . Он также называется самогенерирующим преобразователем, поскольку не требует внешнего источника питания.

Блок-схема активного преобразователя показана на рисунке ниже.

Как показано на рисунке, активный преобразователь будет генерировать электрическую величину (или сигнал), которая эквивалентна неэлектрической входной величине (или сигналу).

Примеры

Ниже приведены примеры активных преобразователей.

• Пьезоэлектрический преобразователь
• Фото Электрический преобразователь
• Термоэлектрический преобразователь

Мы поговорим об этих активных преобразователях в следующей главе.

Пассивные преобразователи

Преобразователь, который не может генерировать электрические величины, такие как напряжение и ток, известен как пассивный преобразователь . Но он производит изменение в одном из пассивных элементов, таких как резистор (R), катушка индуктивности (L) и конденсатор (C). Пассивный преобразователь требует внешнего источника питания.

Блок-схема пассивного преобразователя показана на рисунке ниже.

Как показано на рисунке, пассивный преобразователь будет производить изменение в пассивном элементе в соответствии с изменением неэлектрической входной величины (или сигнала).

Примеры

Ниже приведены примеры пассивных преобразователей.

• Резистивный преобразователь
• Индуктивный преобразователь
• Емкостный преобразователь

Мы поговорим об этих пассивных преобразователях в следующих главах.

Активные преобразователи

Активный преобразователь представляет собой преобразователь, который преобразует неэлектрическую величину в электрическую величину. Давайте рассмотрим неэлектрические величины, такие как давление, освещенность и температура. Следовательно, мы получим следующие три активных преобразователя в зависимости от неэлектрической величины, которую мы выберем.

• Пьезоэлектрический преобразователь
• Фото Электрический преобразователь
• Термоэлектрический преобразователь

Теперь давайте поговорим об этих трех активных преобразователях один за другим.

Пьезоэлектрический преобразователь

Активный преобразователь называется пьезоэлектрическим преобразователем , когда он вырабатывает электрическую величину, эквивалентную давлению на входе. Следующие три вещества проявляют пьезоэлектрический эффект.

• кварцевый
• Соли Рошели
• Турмалин

Пьезоэлектрический эффект, проявляемый этими тремя веществами, — это соли турмалина, кварца и Рошеля в этом возрастающем порядке. В порядке возрастания механической прочности этих трех веществ используются соли Рошеля, Кварц, Турмалин.

Кварц используется в качестве пьезоэлектрического преобразователя, поскольку он проявляет умеренный пьезоэлектрический эффект и обладает умеренной механической прочностью среди этих трех пьезоэлектрических веществ.

Кварцевый преобразователь

Принципиальная схема кварцевого преобразователя показана на рисунке ниже. Как показано на рисунке, кристалл кварца расположен между основанием и элементом суммирования сил. Выходное напряжение может быть измерено на металлических электродах, которые размещены на двух сторонах кварцевого кристалла.

Выходное напряжение $V_ {0}$ вышеуказанного датчика давления будет

$$V_ {0} = \ гидроразрыва {q} {C},$$

Фото Электрический преобразователь

Активный преобразователь называется фотоэлектрическим преобразователем, когда он вырабатывает электрическую величину, которая эквивалентна освещенности входящего света. Принципиальная схема фотоэлектрического преобразователя показана на рисунке ниже.

Работа фотоэлектрического преобразователя упоминается ниже.

• Шаг 1 — Фотоэлектрический преобразователь выпускает электроны, когда свет падает на его катод.

• Шаг 2 — Фотоэлектрический преобразователь создает ток I в цепи из-за притяжения электронов к аноду.

Шаг 1 — Фотоэлектрический преобразователь выпускает электроны, когда свет падает на его катод.

Шаг 2 — Фотоэлектрический преобразователь создает ток I в цепи из-за притяжения электронов к аноду.

Мы можем определить чувствительность фотоэлектрического преобразователя, используя следующую формулу.

$$S = \ гидроразрыва {I} {я}$$

Куда,

$S$ — чувствительность фотоэлектрического преобразователя

$I$ — выходной ток фотоэлектрического преобразователя

$i$ — освещенность светового входа фотоэлектрического преобразователя

Термоэлектрический преобразователь

Активный преобразователь называется термоэлектрическим преобразователем , когда он вырабатывает электрическую величину, эквивалентную температуре на входе. Следующие два преобразователя являются примерами термоэлектрических преобразователей.

• Термисторный преобразователь
• Преобразователь термопары

Теперь давайте поговорим об этих двух преобразователях по одному.

Термисторный преобразователь

Резистор, который зависит от температуры, называется терморезистором. Короче говоря, это называется термистор . Температурный коэффициент термистора отрицательный. Это означает, что с ростом температуры сопротивление термистора уменьшается.

Математически соотношение между сопротивлением термистора и температурой можно представить в виде

$$R_ {1} = R_ {2} e ^ \ left (\ beta \ left [\ frac {1} {T_ {1}} - \ frac {1} {T_ {2}} \ right] \ right)$$

Где

$R_ {1}$ — сопротивление термистора при температуре ${T_ {1}} ^ {0} К$

$R_ {2}$ — сопротивление термистора при температуре ${T_ {2}} ^ {0} К$

$\ beta$ — постоянная температуры

Преимущество термисторного преобразователя заключается в том, что он дает быстрый и стабильный отклик.

Преобразователь термопары

Преобразователь термопары вырабатывает выходное напряжение для соответствующего изменения температуры на входе. Если два провода из разных металлов соединены вместе, чтобы создать два соединения, то вся эта конфигурация называется термопарой . Принципиальная схема базовой термопары показана ниже —

Вышеупомянутая термопара имеет два металла, A & B и два перехода, 1 и 2. Рассмотрим постоянную опорную температуру, $T_ {2}$ на стыке 2. Пусть температура на стыке 1 равна $T_ {1}$. Термопара генерирует ЭДС (электродвижущую силу), когда значения $T_ {1}$ и $T_ {2}$ различны.

Это означает, что термопара генерирует эдс, когда есть разность температур между двумя соединениями, 1 и 2, и она прямо пропорциональна разности температур между этими двумя соединениями. Математически это можно представить как

$$e \ alpha \ left (T_ {1} -T_ {2} \ right)$$

Куда,

$e$ — ЭДС, генерируемая термопарой.

Вышеуказанная схема термопары может быть представлена, как показано на рисунке ниже, для практического применения.

Часть цепи, которая находится между горячими и холодными контактами, включая эти два перехода, является эквивалентной моделью базовой термопары. Гальванометр PMMC подключен через холодный спай и отклоняется в соответствии с ЭДС, генерируемой через холодный спай. Термопарный преобразователь является наиболее часто используемым термоэлектрическим преобразователем.

Пассивные преобразователи

пассивный преобразователь представляет собой преобразователь, который производит изменение пассивного элемента. Мы рассмотрим пассивные элементы, такие как резистор, индуктор и конденсатор. Следовательно, мы получим следующие три пассивных преобразователя в зависимости от выбранного нами пассивного элемента.

• Резистивный преобразователь
• Индуктивный преобразователь
• Емкостный преобразователь

Теперь давайте поговорим об этих трех пассивных преобразователях один за другим.

Резистивный преобразователь

Пассивный преобразователь называется резистивным преобразователем , когда он производит изменение (изменение) значения сопротивления. следующая формула для сопротивления , R металлического проводника.

$$R = \ frac {\ rho \: l} {A}$$

Куда,

$\ rho$ — удельное сопротивление проводника

$l$ — длина проводника

$A$ — площадь поперечного сечения проводника

Значение сопротивления зависит от трех параметров $\ rho, l$ & $A$. Таким образом, мы можем сделать резистивные преобразователи на основе изменения одного из трех параметров $\ rho, l$ & $A$. Изменение любого из этих трех параметров изменяет значение сопротивления.

• Сопротивление R прямо пропорционально удельному сопротивлению проводника, $\ rho$. Таким образом, по мере того как удельное сопротивление проводника, $\ rho$ увеличивает значение сопротивления, R также увеличивается. Аналогично, когда удельное сопротивление проводника, $\ rho$, уменьшает значение сопротивления, R также уменьшается.

• Сопротивление R прямо пропорционально длине проводника, $l$. Таким образом, по мере увеличения длины проводника, $l$ увеличивает значение сопротивления, R также увеличивается. Точно так же, когда длина проводника, $l$, уменьшает значение сопротивления, R также уменьшается.

• Сопротивление R обратно пропорционально площади поперечного сечения проводника, $A$. Так, по мере того, как площадь поперечного сечения проводника, $A$ увеличивает значение сопротивления, R уменьшается. Точно так же, как площадь поперечного сечения проводника, $A$ уменьшает значение сопротивления, R увеличивается.

Сопротивление R прямо пропорционально удельному сопротивлению проводника, $\ rho$. Таким образом, по мере того как удельное сопротивление проводника, $\ rho$ увеличивает значение сопротивления, R также увеличивается. Аналогично, когда удельное сопротивление проводника, $\ rho$, уменьшает значение сопротивления, R также уменьшается.

Сопротивление R прямо пропорционально длине проводника, $l$. Таким образом, по мере увеличения длины проводника, $l$ увеличивает значение сопротивления, R также увеличивается. Точно так же, когда длина проводника, $l$, уменьшает значение сопротивления, R также уменьшается.

Сопротивление R обратно пропорционально площади поперечного сечения проводника, $A$. Так, по мере того, как площадь поперечного сечения проводника, $A$ увеличивает значение сопротивления, R уменьшается. Точно так же, как площадь поперечного сечения проводника, $A$ уменьшает значение сопротивления, R увеличивается.

Индуктивный преобразователь

Пассивный преобразователь называется индуктивным преобразователем , когда он вызывает изменение (изменение) значения индуктивности. следующая формула для индуктивности , L индуктора.

$L = \ frac {N ^ {2}} {S}$ Уравнение 1

Куда,

$N$ — число витков катушки

$S$ — число витков катушки

следующая формула для сопротивления , S катушки.

$S = \ frac {l} {\ mu A}$ Уравнение 2

Куда,

$l$ — длина магнитопровода

$\ mu$ — проницаемость ядра

$A$ — площадь магнитной цепи, через которую течет поток

Заменить уравнение 2 в уравнении 1.

$$L = \ frac {N ^ {2}} {\ left (\ frac {l} {\ mu A} \ right)}$$

$\ Rightarrow L = \ frac {N ^ {2} \ mu A} {l}$ Уравнение 3

Из уравнения 1 и уравнения 3 можно сделать вывод, что значение индуктивности зависит от трех параметров $N, S$ & $\ mu$. Таким образом, мы можем сделать индуктивные преобразователи на основе изменения одного из трех параметров $N, S$ & $\ mu$. Поскольку изменение любого из этих трех параметров изменяет значение индуктивности.

• Индуктивность L прямо пропорциональна квадрату числа витков катушки . Таким образом, по мере увеличения числа витков катушки, $N$ увеличивает значение индуктивности, $L$ также увеличивается. Точно так же, как число витков катушки, $N$ уменьшает значение индуктивности, $L$ также уменьшается.

• Индуктивность, $L$ обратно пропорциональна нежелательности катушки , $S$. Итак, по мере нежелания катушки, $S$ увеличивает значение индуктивности, $L$ уменьшается. Точно так же, как нежелание катушки, $S$ уменьшает значение индуктивности, $L$ увеличивается.

• Индуктивность, L прямо пропорциональна проницаемости сердечника , $\ mu$. Таким образом, по мере проницаемости сердечника, $\ mu$ увеличивает значение индуктивности, L также увеличивается. Точно так же, как проницаемость сердечника, $\ mu$ уменьшает значение индуктивности, L также уменьшается.

Индуктивность L прямо пропорциональна квадрату числа витков катушки . Таким образом, по мере увеличения числа витков катушки, $N$ увеличивает значение индуктивности, $L$ также увеличивается. Точно так же, как число витков катушки, $N$ уменьшает значение индуктивности, $L$ также уменьшается.

Индуктивность, $L$ обратно пропорциональна нежелательности катушки , $S$. Итак, по мере нежелания катушки, $S$ увеличивает значение индуктивности, $L$ уменьшается. Точно так же, как нежелание катушки, $S$ уменьшает значение индуктивности, $L$ увеличивается.

Индуктивность, L прямо пропорциональна проницаемости сердечника , $\ mu$. Таким образом, по мере проницаемости сердечника, $\ mu$ увеличивает значение индуктивности, L также увеличивается. Точно так же, как проницаемость сердечника, $\ mu$ уменьшает значение индуктивности, L также уменьшается.

Емкостный преобразователь

Пассивный преобразователь называется емкостным преобразователем , когда он производит изменение (изменение) значения емкости. следующая формула для емкости C конденсатора с параллельными пластинами.

$$C = \ frac {\ varepsilon A} {d}$$

Куда,

$\ varepsilon$ — диэлектрическая проницаемость или диэлектрическая проницаемость

$A$ — эффективная площадь двух пластин

$d$ — эффективная площадь двух пластин

Значение емкости зависит от трех параметров $\ varepsilon, A$ & $d$. Итак, мы можем сделать емкостные преобразователи на основе изменения одного из трех параметров $\ varepsilon, A$ & $d$. Потому что изменение любого из этих трех параметров меняет значение емкости.

• Емкость, C прямо пропорциональна диэлектрической проницаемости , $\ varepsilon$. Таким образом, в качестве диэлектрической проницаемости $\ varepsilon$ увеличивает значение емкости, C также увеличивается. Точно так же, как диэлектрическая проницаемость, $\ varepsilon$ уменьшает значение емкости, C также уменьшается.

• Емкость, C прямо пропорциональна эффективной площади двух пластин , $A$. Таким образом, поскольку эффективная площадь двух пластин, $A$ увеличивает значение емкости, C также увеличивается. Точно так же, как эффективная площадь двух пластин, $A$ уменьшает значение емкости, C также уменьшается.

• Емкость, C обратно пропорциональна расстоянию между двумя пластинами , $d$. Таким образом, с увеличением расстояния между двумя пластинами $d$ увеличивает значение емкости, а C уменьшается. Точно так же, как расстояние между двумя пластинами, $d$ уменьшает значение емкости, C увеличивается.

Емкость, C прямо пропорциональна диэлектрической проницаемости , $\ varepsilon$. Таким образом, в качестве диэлектрической проницаемости $\ varepsilon$ увеличивает значение емкости, C также увеличивается. Точно так же, как диэлектрическая проницаемость, $\ varepsilon$ уменьшает значение емкости, C также уменьшается.

Емкость, C прямо пропорциональна эффективной площади двух пластин , $A$. Таким образом, поскольку эффективная площадь двух пластин, $A$ увеличивает значение емкости, C также увеличивается. Точно так же, как эффективная площадь двух пластин, $A$ уменьшает значение емкости, C также уменьшается.

Емкость, C обратно пропорциональна расстоянию между двумя пластинами , $d$. Таким образом, с увеличением расстояния между двумя пластинами $d$ увеличивает значение емкости, а C уменьшается. Точно так же, как расстояние между двумя пластинами, $d$ уменьшает значение емкости, C увеличивается.

В этой главе мы обсудили три пассивных преобразователя. В следующей главе давайте обсудим пример для каждого пассивного преобразователя.

Измерение смещения

Физические величины, такие как смещение, скорость, сила, температура и т. Д., Являются неэлектрическими величинами. активный преобразователь преобразует физическую величину в электрический сигнал. Принимая во внимание, что пассивный преобразователь преобразует физическую величину в изменение пассивного элемента.

Таким образом, исходя из требования, мы можем выбрать либо активный датчик, либо пассивный датчик. В этой главе давайте обсудим, как измерить смещение с помощью пассивного преобразователя. Если тело, которое перемещается из одной точки в другую точку по прямой линии, то длина между этими двумя точками называется смещением .

У нас есть следующие три пассивных преобразователя

• Резистивный преобразователь
• Индуктивный преобразователь
• Емкостный преобразователь

Теперь давайте поговорим об измерении смещения с этими тремя пассивными преобразователями по одному.

Измерение смещения с помощью резистивного преобразователя

Принципиальная электрическая схема резистивного преобразователя, который используется для измерения смещения, показана на рисунке ниже.

Вышеуказанная схема состоит из потенциометра и источника напряжения, $V_ {S}$. Можно сказать, что эти два соединены параллельно относительно точек A и B. Потенциометр имеет скользящий контакт, который можно варьировать. Таким образом, точка C является переменной. В приведенной выше схеме выходное напряжение $V_ {0}$ измеряется в точках A и C.

Математически связь между напряжениями и расстояниями может быть представлена ​​как

$$\ гидроразрыва {V_ {0}} {V_ {S}} = \ гидроразрыва {AC} {AB}$$

Поэтому мы должны соединить тело, смещение которого должно быть измерено, со скользящим контактом. Таким образом, всякий раз, когда тело движется по прямой линии, точка C также меняется. Вследствие этого выходное напряжение $V_ {0}$ также изменяется соответствующим образом.

В этом случае мы можем найти смещение, измерив выходное напряжение, $V_ {0}$.

Измерение смещения с использованием индуктивного преобразователя

Принципиальная электрическая схема индуктивного преобразователя, который используется для измерения смещения, показана на рисунке ниже.

Трансформатор, представленный в вышеуказанной цепи, имеет первичную обмотку и две вторичные обмотки. Здесь конечные точки двух вторичных обмоток соединены вместе. Таким образом, мы можем сказать, что эти две вторичные обмотки связаны последовательно .

Напряжение $V_ {P}$ подается на первичную обмотку трансформатора. Пусть напряжение, развиваемое на каждой вторичной обмотке, равно 𠑉 ð’ † 1 и 𠑉 ð’ † 2. Выходное напряжение $V_ {0}$ берется через начальные точки двух вторичных обмоток.

Математически , выходное напряжение » ‰ 0 можно записать в виде

$$V_ {0} = V_ {S1} -V_ {S2}$$

Трансформатор, присутствующий в вышеуказанной схеме, называется дифференциальным трансформатором , поскольку он создает выходное напряжение, которое является разницей между $V_ {S1}$ и $V_ {S2}$.

• Если ядро ​​находится в центральной позиции, то выходное напряжение $V_ {0}$ будет равно нулю. Потому что соответствующие величины и фазы $V_ {S1}$ и $V_ {S2}$ одинаковы.

• Если ядро ​​не находится в центральной позиции, тогда выходное напряжение $V_ {0}$ будет иметь некоторую амплитуду и фазу. Потому что соответствующие величины и фазы $V_ {S1}$ и $V_ {S2}$ не равны.

Если ядро ​​находится в центральной позиции, то выходное напряжение $V_ {0}$ будет равно нулю. Потому что соответствующие величины и фазы $V_ {S1}$ и $V_ {S2}$ одинаковы.

Если ядро ​​не находится в центральной позиции, тогда выходное напряжение $V_ {0}$ будет иметь некоторую амплитуду и фазу. Потому что соответствующие величины и фазы $V_ {S1}$ и $V_ {S2}$ не равны.

Следовательно, мы должны соединить тело, смещение которого должно быть измерено, с центральным ядром. Таким образом, всякий раз, когда тело движется по прямой линии, центральное положение ядра меняется. Вследствие этого выходное напряжение $V_ {0}$ также изменяется соответствующим образом.

В этом случае мы можем найти смещение , измерив выходное напряжение, $V_ {0}$. Величина и фаза выходного напряжения, $V_ {0}$, представляют смещение тела и его направление соответственно.

Измерение смещения с помощью емкостного преобразователя

Принципиальная электрическая схема емкостного преобразователя, который используется для измерения смещения, показана на рисунке ниже.

Конденсатор , который присутствует в вышеуказанной цепи, имеет две параллельные пластины. Среди которых одна пластина закреплена, а другая пластина является подвижной. Из-за этого расстояние между этими двумя пластинами также будет изменяться. значение емкости изменяется при изменении расстояния между двумя пластинами конденсатора.

Поэтому мы должны подключить корпус, смещение которого должно измеряться, к подвижной пластине конденсатора. Таким образом, всякий раз, когда тело движется по прямой линии, расстояние между двумя пластинами конденсатора меняется. Из-за этого значение емкости изменяется.

Системы сбора данных

Системы, используемые для сбора данных, известны как системы сбора данных . Эти системы сбора данных будут выполнять такие задачи, как преобразование данных, хранение данных, передача данных и обработка данных.

Системы сбора данных рассматривают следующие аналоговые сигналы .

• Аналоговые сигналы, которые получаются при прямом измерении электрических величин, таких как постоянный и переменный ток, постоянный и переменный ток, сопротивление и т. Д.

• Аналоговые сигналы, которые получают от преобразователей, таких как LVDT, термопара и т. Д.

Аналоговые сигналы, которые получаются при прямом измерении электрических величин, таких как постоянный и переменный ток, постоянный и переменный ток, сопротивление и т. Д.

Аналоговые сигналы, которые получают от преобразователей, таких как LVDT, термопара и т. Д.

Типы систем сбора данных

Системы сбора данных могут быть классифицированы на следующие два типа .

• Аналоговые системы сбора данных
• Системы сбора цифровых данных

Теперь давайте поговорим об этих двух типах систем сбора данных одна за другой.

Аналоговые системы сбора данных

Системы сбора данных, которые могут работать с аналоговыми сигналами, известны как аналоговые системы сбора данных . Ниже приведены блоки аналоговых систем сбора данных.

• Преобразователь — преобразует физические величины в электрические сигналы.

• Формирователь сигнала — выполняет такие функции, как усиление и выбор требуемой части сигнала.

• Устройство отображения — отображает входные сигналы для целей мониторинга.

• Инструменты для графической записи — они могут использоваться для постоянной записи входных данных.

• Аппаратура на магнитной ленте — используется для сбора, хранения и воспроизведения входных данных.

Преобразователь — преобразует физические величины в электрические сигналы.

Формирователь сигнала — выполняет такие функции, как усиление и выбор требуемой части сигнала.

Устройство отображения — отображает входные сигналы для целей мониторинга.

Инструменты для графической записи — они могут использоваться для постоянной записи входных данных.

Аппаратура на магнитной ленте — используется для сбора, хранения и воспроизведения входных данных.

Системы сбора цифровых данных

Системы сбора данных, которые могут работать с цифровыми сигналами, известны как системы сбора цифровых данных . Таким образом, они используют цифровые компоненты для хранения или отображения информации.

В основном, следующие операции имеют место при сборе цифровых данных.

• Приобретение аналоговых сигналов
• Преобразование аналоговых сигналов в цифровые сигналы или цифровые данные
• Обработка цифровых сигналов или цифровых данных

Ниже приведены блоки цифровых систем сбора данных .

• Преобразователь — преобразует физические величины в электрические сигналы.

• Формирователь сигнала — выполняет такие функции, как усиление и выбор требуемой части сигнала.

• Мультиплексор — подключает один из нескольких входов к выходу. Таким образом, он действует как параллельный последовательный преобразователь.

• Аналого-цифровой преобразователь — преобразует аналоговый вход в эквивалентный цифровой выход.

• Устройство отображения — отображает данные в цифровом формате.

• Цифровой регистратор — используется для записи данных в цифровом формате.

Преобразователь — преобразует физические величины в электрические сигналы.

Формирователь сигнала — выполняет такие функции, как усиление и выбор требуемой части сигнала.

Мультиплексор — подключает один из нескольких входов к выходу. Таким образом, он действует как параллельный последовательный преобразователь.

Аналого-цифровой преобразователь — преобразует аналоговый вход в эквивалентный цифровой выход.

Устройство отображения — отображает данные в цифровом формате.

Цифровой регистратор — используется для записи данных в цифровом формате.

Системы сбора данных используются в различных приложениях, таких как биомедицинские и аэрокосмические. Таким образом, мы можем выбрать либо аналоговые системы сбора данных, либо цифровые системы сбора данных в зависимости от требований.