Другие мосты переменного тока

В предыдущей главе мы обсудили два моста переменного тока, которые можно использовать для измерения индуктивности. В этой главе давайте поговорим о следующих двух мостах переменного тока .

• Мост Шеринг
• Мост Вены

Эти два моста могут быть использованы для измерения емкости и частоты соответственно.

Мост Шеринг

Мост Шеринга представляет собой мост переменного тока, имеющий четыре плеча, которые соединены в форме ромба или квадратной формы , одно плечо которого состоит из одного резистора, одно плечо состоит из последовательной комбинации резистора и конденсатора, одно плечо состоит из одного Конденсатор и другое плечо состоят из параллельной комбинации резистора и конденсатора.

Детектор переменного тока и источник переменного напряжения также используются для определения значения неизвестного импеданса, поэтому один из них расположен на одной диагонали моста Шеринга, а другой — на другой диагонали моста Шеринга.

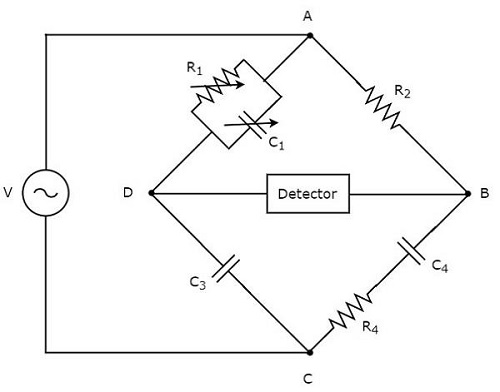
Шеринг-мост используется для измерения значения емкости. Принципиальная схема моста Шеринга показана на рисунке ниже.

В приведенной выше схеме плечи AB, BC, CD и DA вместе образуют ромб или квадратную форму . Плечо AB состоит из резистора, $R_ {2}$. Плечо BC состоит из последовательной комбинации резистора $R_ {4}$ и конденсатора $C_ {4}$. Диск CD состоит из конденсатора $C_ {3}$. Плечо DA состоит из параллельной комбинации резистора $R_ {1}$ и конденсатора $C_ {1}$.

Пусть $Z_ {1}$, $Z_ {2}$, $Z_ {3}$ и $Z_ {4}$ являются импедансами плеч DA, AB, CD и BC соответственно. Значения этих сопротивлений будут

$Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}}$

$\ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}$

$Z_ {2} = R_ {2}$

$Z_ {3} = \ frac {1} {j \ omega C_ {3}}$

$Z_ {4} = R_ {4} + \ frac {1} {j \ omega C_ {4}}$

$\ Rightarrow Z_ {4} = \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}}$

Замените эти значения импеданса в следующем условии балансировки моста переменного тока.

$$Z_ {4} = \ гидроразрыва {Z_ {2} Z_ {3}} {Z_ {1}}$$

$$\ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (\ frac {1} {j \ omega C_ { 3}} \ right)} {\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}}$$

$\ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {j \ omega C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {j \ omega R_ {1} C_ {3}}$

$\ Rightarrow \ frac {1 + j \ omega R_ {4} C_ {4}} {C_ {4}} = \ frac {R_ {2} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ {1} C_ {3}}$

$\ Rightarrow \ frac {1} {C_ {4}} + j \ omega R_ {4} = \ frac {R_ {2}} {R_ {1} C_ {3}} + \ frac {j \ omega C_ { 1} R_ {2}} {C_ {3}}$

Сравнивая соответствующие вещественные и мнимые члены вышеприведенного уравнения, получим

$C_ {4} = \ frac {R_ {1} C_ {3}} {R_ {2}}$ Уравнение 1

$R_ {4} = \ frac {C_ {1} R_ {2}} {C_ {3}}$ Уравнение 2

Подставляя значения $R_ {1}, R_ {2}$ и $C_ {3}$ в уравнение 1, мы получим значение конденсатора, $C_ {4}$. Аналогично, подставляя значения уравнения $R_ {2}, C_ {1}$ и $C_ {3}$ в уравнение 2, мы получим значение резистора, $R_ {4}$.

Преимущество моста Шеринга состоит в том, что оба значения резистора, $R_ {4}$ и конденсатора, $C_ {4}$, не зависят от значения частоты.

Мост Вены

Мост Вена — это мост переменного тока, имеющий четыре плеча, которые связаны в форме ромба или квадратной формы. Среди двух плеч состоит из одного резистора, один плечо состоит из параллельной комбинации резистора и конденсатора, а другой плечо состоит из последовательной комбинации резистора и конденсатора.

Детектор переменного тока и источник переменного напряжения также необходимы для того, чтобы найти значение частоты. Следовательно, один из этих двух находится в одной диагонали моста Вена, а другой — в другой диагонали моста Вена.

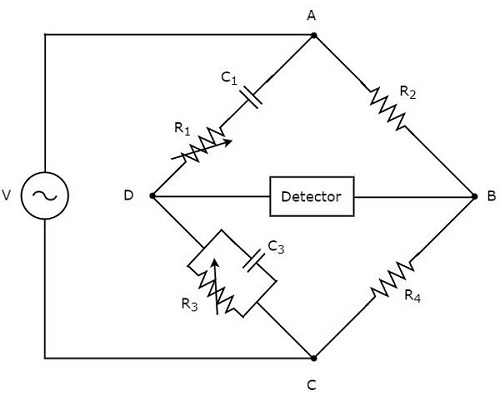
Принципиальная схема моста Вена показана на рисунке ниже.

В приведенной выше схеме плечи AB, BC, CD и DA вместе образуют ромб или квадратную форму . Плечи, AB и BC состоят из резисторов, $R_ {2}$ и $R_ {4}$ соответственно. Плечо CD состоит из параллельной комбинации резистора $R_ {3}$ и конденсатора $C_ {3}$. Плечо DA состоит из последовательной комбинации резистора $R_ {1}$ и конденсатора $C_ {1}$.

Пусть $Z_ {1}, Z_ {2}, Z_ {3}$ и $Z_ {4}$ являются импедансами плеч DA, AB, CD и BC соответственно. Значения этих сопротивлений будут

$$Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}}$$

$$\ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}}$$

$Z_ {2} = R_ {2}$

$$Z_ {3} = \ frac {R_ {3} \ left (\ frac {1} {j \ omega C_ {3}} \ right)} {R_ {3} + \ frac {1} {j \ omega C_ {3}}}$$

$$\ Rightarrow Z_ {3} = \ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}}$$

$Z_ {4} = R_ {4}$

Замените эти значения импеданса в следующем условии балансировки моста переменного тока.

$$Z_ {1} Z_ {4} = Z_ {2} Z_ {3}$$

$$\ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} \ right) R_ {4} = R_ {2} \ left (\ frac {R_ {3}} {1 + j \ omega R_ {3} C_ {3}} \ right)$$

$\ Rightarrow \ left (1 + j \ omega R_ {1} C_ {1} \ right) \ left (1 + j \ omega R_ {3} C_ {3} \ right) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3}$

$\ Rightarrow \ left (1 + j \ omega R_ {3} C_ {3} + j \ omega R_ {1} C_ {1} - \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) R_ {4} = j \ omega C_ {1} R_ {2} R_ {3}$

$\ Rightarrow R_ {4} \ left (\ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) + j \ omega R_ {4} \ left (R_ {3} C_ {3} + R_ {1} C_ {1} \ right) = j \ omega C_ {1} R_ {2} R_ {3}$

Приравнять соответствующие реальные члены вышеприведенного уравнения.

$$R_ {4} \ left (1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} \ right) = 0$$

$\ Rightarrow 1- \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3} = 0$

$\ Rightarrow 1 = \ omega ^ {2} R_ {1} R_ {3} C_ {1} C_ {3}$

$\ omega = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}}$

Замените $\ omega = 2 \ pi f$ в вышеприведенном уравнении.

$$\ Rightarrow 2 \ pi f = \ frac {1} {\ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}}$$

$\ Rightarrow f = \ frac {1} {2 \ pi \ sqrt {R_ {1} R_ {3} C_ {1} C_ {3}}}$

Мы можем найти значение частоты, $f$ источника переменного напряжения, подставив в вышеприведенное уравнение значения $R_ {1}, R_ {3}, C_ {1}$ и $C_ {3}$.

Если $R_ {1} = R_ {3} = R$ и $C_ {1} = C_ {3} = C$, то мы можем найти значение частоты, $f$ источника переменного напряжения, используя следующую формулу ,

$$f = \ frac {1} {2 \ pi RC}$$

Мост Вейна в основном используется для определения значения частоты диапазона АФ.