Учебники

NP Hard и NP-Complete Классы

Июль 31, 2018

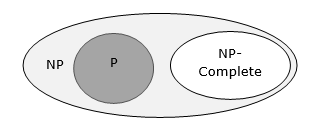
Проблема в классе NPC, если она в NP и такая же сложная, как любая проблема в NP. Проблема является NP-трудной, если все проблемы в NP сводятся к ней за полиномиальное время, даже если она не может быть в самой NP.

NP-трудной

Если для любой из этих задач существует алгоритм полиномиального времени, все задачи в NP будут решаться за полиномиальное время. Эти проблемы называются NP-полными . Феномен NP-полноты важен как по теоретическим, так и по практическим причинам.

Определение NP-полноты

Язык B является NP-полным, если он удовлетворяет двум условиям

  • Б находится в НП

  • Каждое A в NP является полиномиальным временем, приводимым к B.

Б находится в НП

Каждое A в NP является полиномиальным временем, приводимым к B.

Если язык удовлетворяет второму свойству, но не обязательно первому, язык B называется NP-Hard . Неформально, проблема поиска B является NP-трудной, если существует некоторая NP-полная проблема A, которую Тьюринг сводит к B.

Проблема в NP-Hard не может быть решена за полиномиальное время, пока P = NP . Если проблема оказывается NPC, нет необходимости тратить время на поиск эффективного алгоритма для нее. Вместо этого мы можем сосредоточиться на алгоритме аппроксимации дизайна.

NP-полные задачи

Ниже приведены некоторые задачи NP-Complete, для которых не известен алгоритм полиномиального времени.

  • Определение, имеет ли граф гамильтонов цикл
  • Определение того, является ли булева формула выполнимой и т. Д.

NP-сложные проблемы

Следующие проблемы являются NP-Hard

  • Проблема выполнимости схемы
  • Установить обложку
  • Вершинное покрытие
  • Задача коммивояжера

В этом контексте, теперь мы обсудим TSP является NP-Complete

TSP является NP-Complete

Задача коммивояжера состоит из коммивояжера и множества городов. Продавец должен посетить каждый из городов, начиная с определенного и возвращаясь в тот же город. Проблема в том, что коммивояжёр хочет минимизировать общую длину поездки.

доказательство

Чтобы доказать, что TSP является NP-Complete , сначала мы должны доказать, что TSP принадлежит NP . В TSP мы находим тур и проверяем, что тур содержит каждую вершину один раз. Затем рассчитывается общая стоимость краев тура. Наконец, мы проверяем, является ли стоимость минимальной. Это может быть выполнено за полиномиальное время. Таким образом, TSP принадлежит NP .

Во-вторых, мы должны доказать, что TSP NP-сложен . Чтобы доказать это, можно показать, что гамильтонов цикл ≤ p TSP (поскольку мы знаем, что задача о гамильтоновом цикле NP-полна).

Предположим, что G = (V, E) является экземпляром гамильтонова цикла.

Следовательно, экземпляр TSP построен. Создаем полный граф G ‘ = (V, E ‘ ) , где

E′= lbrace(i,j) двоеточиеi,j inVиi neqj

Таким образом, функция стоимости определяется следующим образом:

t (i, j) = \ begin {case} 0 & if \: (i, j) \: \ in E \\ 1 & в противном случае \ end {case}

Предположим теперь, что в G существует гамильтонов цикл. Ясно, что стоимость каждого ребра в h равна 0 в G ‘, поскольку каждое ребро принадлежит E. Следовательно, h имеет стоимость 0 в G ‘ . Таким образом, если у графа G есть гамильтонов цикл, то у графа G ‘ тур 0 стоимости.

И наоборот, мы предполагаем, что G ‘ имеет тур h ‘ стоимости не более 0 . Стоимость ребер в E ‘ равна 0 и 1 по определению. Следовательно, каждое ребро должно иметь стоимость 0, поскольку стоимость h ‘ равна 0 . Поэтому мы заключаем, что h ‘ содержит только ребра в E.

Таким образом, мы доказали, что G имеет гамильтонов цикл, если и только если G ‘ имеет обход стоимости не более 0 . TSP является NP-полной.

69
Share: