Чтобы вставить элемент в кучу, новый элемент изначально добавляется в конец кучи как последний элемент массива.
После вставки этого элемента свойство heap может быть нарушено, следовательно, свойство heap восстанавливается путем сравнения добавленного элемента с его родительским элементом и перемещения добавленного элемента на уровень, меняя позиции с родительским. Этот процесс называется перколяцией .
Сравнение повторяется до тех пор, пока родительский элемент не станет больше или равен перколирующему элементу.
Algorithm: Max-Heap-Insert (numbers[], key) heapsize = heapsize + 1 numbers[heapsize] = -∞ i = heapsize numbers[i] = key while i > 1 and numbers[Parent(numbers[], i)] < numbers[i] exchange(numbers[i], numbers[Parent(numbers[], i)]) i = Parent (numbers[], i)
Анализ
Первоначально, элемент добавляется в конец массива. Если он нарушает свойство heap, элемент обменивается с его родителем. Высота дерева равна log n . Максимальный журнал n количество операций, которые необходимо выполнить.
Следовательно, сложность этой функции составляет O (log n) .
пример
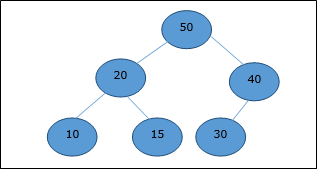
Давайте рассмотрим максимальную кучу, как показано ниже, где необходимо добавить новый элемент 5.
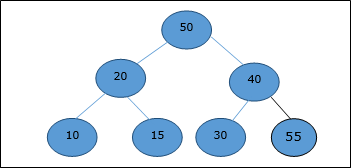
Первоначально 55 будет добавлено в конце этого массива.
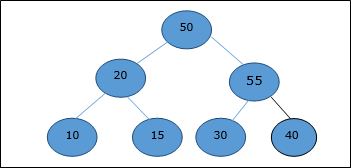
После вставки он нарушает свойство кучи. Следовательно, элемент должен поменяться с его родителем. После подкачки куча выглядит следующим образом.
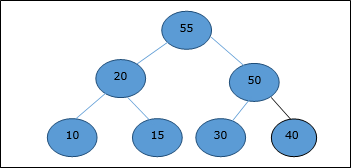
Опять же, элемент нарушает свойство кучи. Следовательно, он поменяется с родителем.
Теперь мы должны остановиться.