Объедините набор отсортированных файлов разной длины в один отсортированный файл. Нам нужно найти оптимальное решение, где результирующий файл будет сгенерирован за минимальное время.
Если указано количество отсортированных файлов, существует много способов объединить их в один отсортированный файл. Это слияние может быть выполнено парами. Следовательно, этот тип слияния называется двухсторонними шаблонами слияния .
Поскольку разные пары требуют разного количества времени, в этой стратегии мы хотим определить оптимальный способ объединения множества файлов. На каждом шаге объединяются две самые короткие последовательности.
Чтобы объединить файл p-записи и файл q-записи, возможно, потребуется перемещение записей p + q , очевидный выбор которого заключается в объединении двух самых маленьких файлов вместе на каждом шаге.
Шаблоны двустороннего слияния могут быть представлены двоичными деревьями слияния. Рассмотрим набор из n отсортированных файлов {f 1 , f 2 , f 3 ,…, f n } . Первоначально каждый элемент этого рассматривается как двоичное дерево одного узла. Чтобы найти это оптимальное решение, используется следующий алгоритм.
Algorithm: TREE (n) for i := 1 to n – 1 do declare new node node.leftchild := least (list) node.rightchild := least (list) node.weight) := ((node.leftchild).weight) + ((node.rightchild).weight) insert (list, node); return least (list);
В конце этого алгоритма вес корневого узла представляет собой оптимальную стоимость.
пример
Рассмотрим данные файлы, f 1 , f 2 , f 3 , f 4 и f 5 с 20, 30, 10, 5 и 30 количеством элементов соответственно.
Если операции слияния выполняются в соответствии с предоставленной последовательностью, то
M 1 = объединить f 1 и f 2 => 20 + 30 = 50
M 2 = объединить M 1 и f 3 => 50 + 10 = 60
М 3 = объединить М 2 и f 4 => 60 + 5 = 65
М 4 = объединить М 3 и f 5 => 65 + 30 = 95
Следовательно, общее количество операций
50 + 60 + 65 + 95 = 270
Теперь возникает вопрос, есть ли лучшее решение?
Сортируя числа по размеру в порядке возрастания, получаем следующую последовательность:
f 4 , f 3 , f 1 , f 2 , f 5
Следовательно, операции слияния могут быть выполнены на этой последовательности
M 1 = объединить f 4 и f 3 => 5 + 10 = 15
M 2 = объединить M 1 и f 1 => 15 + 20 = 35
М 3 = объединить М 2 и f 2 => 35 + 30 = 65
М 4 = объединить М 3 и f 5 => 65 + 30 = 95
Следовательно, общее количество операций
15 + 35 + 65 + 95 = 210
Очевидно, это лучше, чем предыдущий.
В этом контексте мы сейчас собираемся решить проблему, используя этот алгоритм.
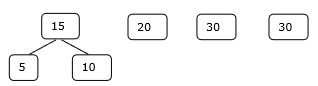
Начальный набор
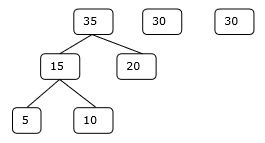
Шаг 1
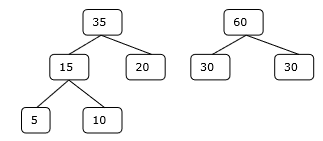
Шаг 2
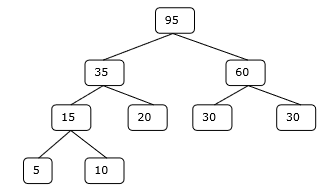
Шаг 3
Шаг 4
Следовательно, решение занимает 15 + 35 + 60 + 95 = 205 количество сравнений.