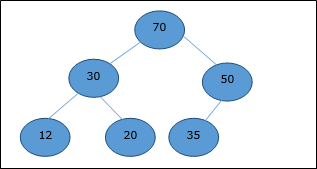
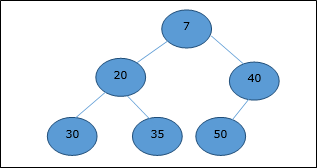
Существует несколько типов куч, однако в этой главе мы собираемся обсудить двоичную кучу. Бинарная куча — это структура данных, которая выглядит как полное двоичное дерево. Структура данных кучи подчиняется свойствам упорядочения, описанным ниже. Обычно куча представлена массивом. В этой главе мы представляем кучу H.
Поскольку элементы кучи хранятся в массиве, учитывая начальный индекс как 1 , положение родительского узла i- го элемента можно найти в ⌊ i / 2 ⌋ . Левый и правый дочерние элементы i- го узла находятся в положении 2i и 2i + 1 .
Двоичная куча может быть классифицирована далее как максимальная куча или минимальная куча на основе свойства упорядочения.
Max-Heap
В этой куче значение ключа узла больше или равно значению ключа самого высокого дочернего элемента.
Следовательно, H [Parent (i)] ≥ H [i]
Min-Heap
В средней куче значение ключа узла меньше или равно значению ключа самого нижнего потомка.
Следовательно, H [Parent (i)] ≤ H [i]
В этом контексте основные операции показаны ниже относительно Max-Heap. Для вставки и удаления элементов в кучах и из них требуется перестановка элементов. Следовательно, функция Heapify должна быть вызвана.
Представление массива
Полное двоичное дерево может быть представлено массивом, хранящим его элементы с использованием обхода порядка уровней.
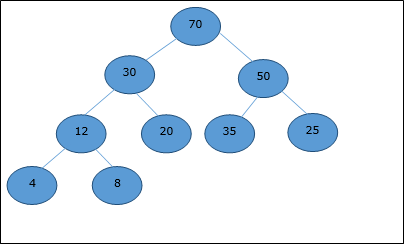
Давайте рассмотрим кучу (как показано ниже), которая будет представлена массивом H.
Рассматривая начальный индекс как 0 , используя обход уровня, элементы сохраняются в массиве следующим образом.
| Индекс | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| элементы | 70 | 30 | 50 | 12 | 20 | 35 | 25 | 4 | 8 | … |
В этом контексте операции с кучей представляются в отношении Max-Heap.
Чтобы найти индекс родителя элемента по индексу i , используется следующий алгоритм Parent (numbers [], i) .
Algorithm: Parent (numbers[], i) if i == 1 return NULL else [i / 2]
Индекс левого потомка элемента с индексом i можно найти с помощью следующего алгоритма Left-Child (numbers [], i) .
Algorithm: Left-Child (numbers[], i) If 2 * i ≤ heapsize return [2 * i] else return NULL
Индекс правого потомка элемента по индексу i можно найти с помощью следующего алгоритма Right-Child (numbers [], i) .