Покрытие вершины неориентированного графа G = (V, E) является подмножеством вершин V ‘ ⊆ V таким, что если ребро (u, v) является ребром G , то либо u в V, либо v в V ‘, либо и то и другое.
Найти покрытие вершины максимального размера в данном неориентированном графе. Это оптимальное вершинное раскрытие является оптимизационной версией NP-полной задачи. Однако не так сложно найти покрытие вершин, близкое к оптимальному.
APPROX-VERTEX_COVER (G: Graph) c ← { } E ' ← E[G]
while E ' is not empty do
Let (u, v) be an arbitrary edge of E ' c ← c U {u, v}
Remove from E ' every edge incident on either u or v
return c
пример
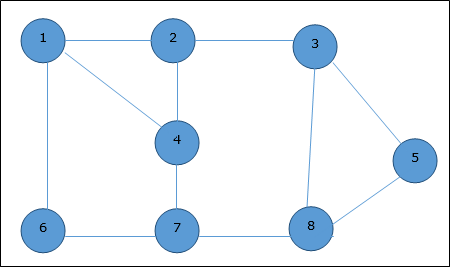
Множество ребер данного графа —
{(1,6), (1,2), (1,4), (2,3), (2,4), (6,7), (4,7), (7,8), ( 3,8), (3,5), (8,5)}
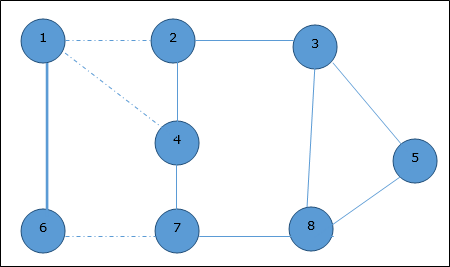
Теперь мы начнем с выбора произвольного ребра (1,6). Мы удаляем все ребра, которые либо падают на вершину 1 или 6, и добавляем ребро (1,6) для покрытия.
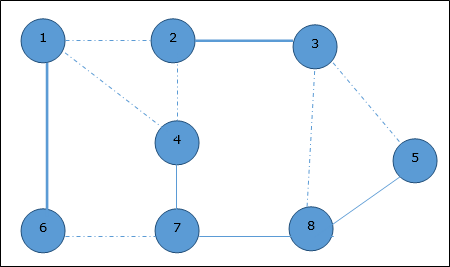
На следующем шаге мы выбрали другое ребро (2,3) наугад
Теперь мы выбираем другое ребро (4,7).
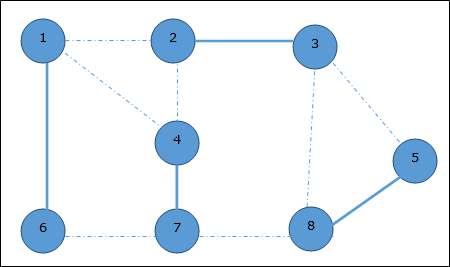
Выбираем другое ребро (8,5).
Следовательно, вершинное покрытие этого графа равно {1,2,4,5}.
Анализ
Легко видеть, что время выполнения этого алгоритма составляет O (V + E) , используя список смежности для представления E ‘ .