DAA — Введение

Алгоритм — это набор шагов операций для решения задачи, связанной с выполнением вычислений, обработкой данных и задачами автоматического рассуждения. Алгоритм является эффективным методом, который может быть выражен в течение ограниченного времени и пространства.

Алгоритм — лучший способ представить решение конкретной задачи очень простым и эффективным способом. Если у нас есть алгоритм для конкретной задачи, то мы можем реализовать его на любом языке программирования, а это означает, что алгоритм не зависит от каких-либо языков программирования .

Разработка алгоритма

Важные аспекты разработки алгоритма включают создание эффективного алгоритма для эффективного решения проблемы с использованием минимального времени и пространства.

Чтобы решить проблему, можно использовать разные подходы. Некоторые из них могут быть эффективными с точки зрения затрат времени, тогда как другие подходы могут быть эффективными с точки зрения памяти. Однако следует иметь в виду, что и потребление времени, и использование памяти не могут быть оптимизированы одновременно. Если нам требуется, чтобы алгоритм выполнялся за меньшее время, мы должны вкладывать больше памяти, а если нам требуется алгоритм для работы с меньшей памятью, нам нужно больше времени.

Этапы разработки проблемы

Следующие шаги участвуют в решении вычислительных задач.

• Определение проблемы
• Разработка модели
• Спецификация алгоритма
• Разработка алгоритма
• Проверка правильности алгоритма
• Анализ алгоритма
• Реализация алгоритма
• Тестирование программы
• Документация

Характеристики алгоритмов

Основные характеристики алгоритмов следующие:

• Алгоритмы должны иметь уникальное имя

• Алгоритмы должны иметь четко определенный набор входов и выходов

• Алгоритмы хорошо упорядочены с однозначными операциями

• Алгоритмы останавливаются за конечное время. Алгоритмы не должны работать бесконечно, т. Е. Алгоритм должен заканчиваться в некоторой точке

Алгоритмы должны иметь уникальное имя

Алгоритмы должны иметь четко определенный набор входов и выходов

Алгоритмы хорошо упорядочены с однозначными операциями

Алгоритмы останавливаются за конечное время. Алгоритмы не должны работать бесконечно, т. Е. Алгоритм должен заканчиваться в некоторой точке

ПСЕВДОКОД

Псевдокод дает общее описание алгоритма без неоднозначности, связанной с простым текстом, но также без необходимости знать синтаксис конкретного языка программирования.

Время выполнения может быть оценено в более общем виде с использованием псевдокода для представления алгоритма в виде набора фундаментальных операций, которые затем могут быть подсчитаны.

Разница между алгоритмом и псевдокодом

Алгоритм — это формальное определение с некоторыми специфическими характеристиками, которое описывает процесс, который может быть выполнен компьютером-машиной Тьюринга для выполнения конкретной задачи. Как правило, слово «алгоритм» может использоваться для описания любой задачи высокого уровня в области компьютерных наук.

С другой стороны, псевдокод — это неформальное и (часто рудиментарное) удобочитаемое описание алгоритма, оставляющее много детальных деталей о нем. Написание псевдокода не имеет ограничений по стилям, и его единственная цель — описать шаги алгоритма высокого уровня в очень реалистичной манере на естественном языке.

Например, ниже приведен алгоритм сортировки вставок.

Algorithm: Insertion-Sort 
Input: A list L of integers of length n  
Output: A sorted list L1 containing those integers present in L 
Step 1: Keep a sorted list L1 which starts off empty  
Step 2: Perform Step 3 for each element in the original list L  
Step 3: Insert it into the correct position in the sorted list L1.  
Step 4: Return the sorted list 
Step 5: Stop

Вот псевдокод, который описывает, как высокоуровневый абстрактный процесс, упомянутый выше в алгоритме Insertion-Sort, может быть описан более реалистичным образом.

for i <- 1 to length(A) 
   x <- A[i] 
   j <- i 
   while j > 0 and A[j-1] > x 
      A[j] <- A[j-1] 
      j <- j - 1 
   A[j] <- x

В этом руководстве алгоритмы будут представлены в виде псевдокода, который во многом похож на C, C ++, Java, Python и другие языки программирования.

DAA — анализ алгоритмов

При теоретическом анализе алгоритмов принято оценивать их сложность в асимптотическом смысле, т. Е. Оценивать функцию сложности для произвольно больших входных данных. Термин «анализ алгоритмов» был придуман Дональдом Кнутом.

Алгоритм анализа является важной частью теории вычислительной сложности, которая обеспечивает теоретическую оценку необходимых ресурсов алгоритма для решения конкретной вычислительной задачи. Большинство алгоритмов предназначены для работы с входами произвольной длины. Анализ алгоритмов — это определение количества временных и пространственных ресурсов, необходимых для его выполнения.

Обычно эффективность или время выполнения алгоритма указывается как функция, связывающая длину ввода с числом шагов, известных как временная сложность , или объем памяти, известный как пространственная сложность .

Необходимость анализа

В этой главе мы обсудим необходимость анализа алгоритмов и способы выбора лучшего алгоритма для конкретной задачи, поскольку одна вычислительная задача может быть решена различными алгоритмами.

Рассматривая алгоритм для конкретной задачи, мы можем начать развивать распознавание образов, чтобы с помощью этого алгоритма можно было решать похожие проблемы.

Алгоритмы часто сильно отличаются друг от друга, хотя цель этих алгоритмов одна и та же. Например, мы знаем, что набор чисел может быть отсортирован с использованием разных алгоритмов. Количество сравнений, выполненных одним алгоритмом, может отличаться от других для одного и того же ввода. Следовательно, временная сложность этих алгоритмов может отличаться. В то же время нам необходимо рассчитать объем памяти, необходимый для каждого алгоритма.

Анализ алгоритма — это процесс анализа способности алгоритма решать задачи с точки зрения требуемого времени и размера (объема памяти для хранения при реализации). Однако основной проблемой анализа алгоритмов является требуемое время или производительность. Как правило, мы выполняем следующие виды анализа —

• В худшем случае — максимальное количество шагов, предпринятых для любого экземпляра размера a .

• Наилучший вариант — минимальное количество шагов, предпринимаемых для любого экземпляра размера a .

• Средний случай — среднее количество шагов, предпринятых для любого экземпляра размера a .

• Амортизация — последовательность операций, применяемая к усредненному по времени вводу размера.

В худшем случае — максимальное количество шагов, предпринятых для любого экземпляра размера a .

Наилучший вариант — минимальное количество шагов, предпринимаемых для любого экземпляра размера a .

Средний случай — среднее количество шагов, предпринятых для любого экземпляра размера a .

Амортизация — последовательность операций, применяемая к усредненному по времени вводу размера.

Чтобы решить проблему, мы должны учитывать время и сложность пространства, так как программа может работать в системе, где память ограничена, но имеется достаточно места или может быть наоборот. В этом контексте, если мы сравниваем сортировку пузырьков и сортировку слиянием . Пузырьковая сортировка не требует дополнительной памяти, но сортировка слиянием требует дополнительного пространства. Хотя временная сложность пузырьковой сортировки выше по сравнению с сортировкой слиянием, нам может потребоваться применить пузырьковую сортировку, если программа должна работать в среде, где память очень ограничена.

DAA — методология анализа

Чтобы измерить потребление ресурсов алгоритмом, используются разные стратегии, как описано в этой главе.

Асимптотический анализ

Асимптотическое поведение функции f (n) относится к росту f (n), когда n становится большим.

Обычно мы игнорируем небольшие значения n , так как мы обычно заинтересованы в оценке того, насколько медленной будет программа при больших входах.

Хорошее эмпирическое правило заключается в том, что чем ниже скорость асимптотического роста, тем лучше алгоритм. Хотя это не всегда так.

Например, линейный алгоритм $f (n) = d * n + k$ всегда асимптотически лучше квадратичного, $f (n) = cn ^ 2 + q$.

Решение рекуррентных уравнений

Повторение — это уравнение или неравенство, которое описывает функцию в терминах ее значения на меньших входах. Рецидивы обычно используются в парадигме «разделяй и властвуй».

Рассмотрим T (n) как время выполнения задачи размера n .

Если размер задачи достаточно мал, скажем, n <c, где c — константа, прямое решение занимает постоянное время, которое записывается как θ (1) . Если разделение задачи приводит к ряду подзадач с размером $\ frac {n} {b}$.

Для решения проблемы требуется время aT (n / b) . Если мы считаем, что время, необходимое для деления, равно D (n), а время, необходимое для объединения результатов подзадач, — C (n) , рекуррентное соотношение можно представить в виде —

$$Т (п) = \ {начинаются случаи} \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \ theta (1) &amp;amp; if \: n \ leqslant c \\ a T (\ frac {n} {b}) + D (n) + C (n) и в противном случае \ end { случаи}$$

Рекуррентное отношение может быть решено с использованием следующих методов:

• Метод замещения — В этом методе мы угадываем границу и, используя математическую индукцию, доказываем, что наше предположение было верным.

• Метод дерева рекурсии — В этом методе формируется дерево рекурсии, где каждый узел представляет стоимость.

• Теорема магистрата — это еще один важный метод, позволяющий найти сложность рекуррентного отношения.

Метод замещения — В этом методе мы угадываем границу и, используя математическую индукцию, доказываем, что наше предположение было верным.

Метод дерева рекурсии — В этом методе формируется дерево рекурсии, где каждый узел представляет стоимость.

Теорема магистрата — это еще один важный метод, позволяющий найти сложность рекуррентного отношения.

Амортизированный анализ

Амортизированный анализ обычно используется для определенных алгоритмов, в которых выполняется последовательность похожих операций.

• Амортизированный анализ обеспечивает оценку фактической стоимости всей последовательности, а не оценку стоимости последовательности операций отдельно.

• Амортизированный анализ отличается от анализа среднего случая; Вероятность не участвует в амортизированном анализе. Амортизированный анализ гарантирует среднюю производительность каждой операции в худшем случае.

Амортизированный анализ обеспечивает оценку фактической стоимости всей последовательности, а не оценку стоимости последовательности операций отдельно.

Амортизированный анализ отличается от анализа среднего случая; Вероятность не участвует в амортизированном анализе. Амортизированный анализ гарантирует среднюю производительность каждой операции в худшем случае.

Это не просто инструмент для анализа, это способ мышления о дизайне, поскольку проектирование и анализ тесно связаны.

Совокупный метод

Агрегатный метод дает глобальное представление о проблеме. В этом методе, если n операций занимает общее время времени наихудшего случая T (n) . Тогда амортизированная стоимость каждой операции равна T (n) / n . Хотя разные операции могут занимать разное время, в этом методе игнорируются различные затраты.

Метод учета

В этом методе разные операции назначаются разным операциям в соответствии с их фактической стоимостью. Если амортизированная стоимость операции превышает ее фактическую стоимость, разница присваивается объекту как кредит. Этот кредит помогает оплачивать последующие операции, для которых амортизированная стоимость меньше реальной стоимости.

Если фактическая стоимость и амортизированная стоимость i- ^й операции составляют $c_ {i}$ и $\ hat {c_ {l}}$, то

$$\ displaystyle \ sum \ limit_ {i = 1} ^ n \ hat {c_ {l}} \ geqslant \ displaystyle \ sum \ limit_ {i = 1} ^ n c_ {i}$$

Потенциальный метод

Этот метод представляет предоплаченную работу как потенциальную энергию, а не рассматривает предоплаченную работу в качестве кредита. Эта энергия может быть выпущена для оплаты будущих операций.

Если мы выполним n операций, начиная с исходной структуры данных D ₀ . Рассмотрим, c _i — фактическую стоимость, а D _i — структуру данных i- ^й операции. Потенциальная функция Ф отображается в действительное число Ф ( D _i ), связанный потенциал D _i . Амортизированная стоимость $\ hat {c_ {l}}$ может быть определена как

$$\ hat {c_ {l}} = c_ {i} + \ Phi (D_ {i}) - \ Phi (D_ {i-1})$$

Следовательно, общая амортизированная стоимость

$$ \ displaystyle \ sum \ limit_ {i = 1} ^ n \ hat {c_ {l}} = \ displaystyle \ sum \ limit_ {i = 1} ^ n (c_ {i} + \ Phi (D_ {i}) ) — \ Phi (D_ {i-1})) = \ displaystyle \ sum \ limit_ {i = 1} ^ n c_ {i} + \ Phi (D_ {n}) — \ Phi (D_ {0}) $ $

Динамическая таблица

Если выделенного пространства для таблицы недостаточно, мы должны скопировать таблицу в таблицу большего размера. Аналогично, если из таблицы удаляется большое количество элементов, рекомендуется перераспределить таблицу меньшего размера.

Используя амортизированный анализ, мы можем показать, что амортизированная стоимость вставки и удаления постоянна, а неиспользуемое пространство в динамической таблице никогда не превышает постоянной доли общего пространства.

В следующей главе этого руководства мы кратко обсудим асимптотические обозначения.

Асимптотические обозначения и априорный анализ

При разработке Алгоритма анализ сложности алгоритма является существенным аспектом. Главным образом, сложность алгоритма связана с его производительностью, с тем, насколько быстро или медленно он работает.

Сложность алгоритма описывает эффективность алгоритма с точки зрения объема памяти, необходимой для обработки данных, и времени обработки.

Сложность алгоритма анализируется в двух ракурсах: время и пространство .

Сложность времени

Это функция, описывающая количество времени, необходимое для запуска алгоритма, с точки зрения размера ввода. «Время» может означать количество выполненных обращений к памяти, количество сравнений между целыми числами, количество выполнений некоторого внутреннего цикла или некоторую другую натуральную единицу, связанную с количеством реального времени, которое займет алгоритм.

Космическая сложность

Это функция, описывающая объем памяти, занимаемый алгоритмом с точки зрения размера ввода в алгоритм. Мы часто говорим о «дополнительной» необходимой памяти, не считая памяти, необходимой для хранения самого ввода. Опять же, мы используем натуральные (но фиксированной длины) единицы измерения для этого.

Сложность пространства иногда игнорируется, поскольку используемое пространство минимально и / или очевидно, однако иногда оно становится такой же важной проблемой, как и время.

Асимптотические обозначения

Время выполнения алгоритма зависит от набора команд, скорости процессора, скорости дискового ввода-вывода и т. Д. Следовательно, мы оцениваем эффективность алгоритма асимптотически.

Функция времени алгоритма представлена ​​как T (n) , где n — размер ввода.

Различные типы асимптотических обозначений используются для представления сложности алгоритма. Следующие асимптотические обозначения используются для вычисления сложности времени выполнения алгоритма.

• О — Большой О

• Ω — большая омега

• θ — большая тета

• о — маленький о

• ω — маленькая омега

О — Большой О

Ω — большая омега

θ — большая тета

о — маленький о

ω — маленькая омега

O: асимптотическая верхняя граница

«О» (Big Oh) — наиболее часто используемая запись. Функция f (n) может быть представлена ​​в следующем порядке: g (n), то есть O (g (n)) , если существует значение положительного целого числа n, равного n _0, и положительной константы c, такой что —

$f (n) \ leqslant cg (n)$ для $n&amp;gt; n_ {0}$ во всех случаях

Следовательно, функция g (n) является верхней границей для функции f (n) , так как g (n) растет быстрее, чем f (n) .

пример

Рассмотрим данную функцию: $f (n) = 4.n ^ 3 + 10.n ^ 2 + 5.n + 1$

Учитывая, что $g (n) = n ^ 3$,

$f (n) \ leqslant 5.g (n)$ для всех значений $n&amp;gt; 2$

Следовательно, сложность f (n) может быть представлена ​​в виде $O (g (n))$, то есть $O (n ^ 3)$

Ω: асимптотическая нижняя граница

Мы говорим, что $f (n) = \ Omega (g (n))$, когда существует постоянная c, что $f (n) \ geqslant cg (n)$ для всех достаточно больших значений n . Здесь n — положительное целое число. Это означает, что функция g является нижней границей для функции f ; после определенного значения n f никогда не опустится ниже g .

пример

Рассмотрим данную функцию: $f (n) = 4.n ^ 3 + 10.n ^ 2 + 5.n + 1$.

Учитывая $g (n) = n ^ 3$, $f (n) \ geqslant 4.g (n)$ для всех значений $n&amp;gt; 0$.

Следовательно, сложность f (n) может быть представлена ​​в виде $\ Omega (g (n))$, то есть $\ Omega (n ^ 3)$

θ: асимптотическая жесткая граница

Мы говорим, что $f (n) = \ theta (g (n))$, когда существуют константы c ₁ и c _2, которые $c_ {1} .g (n) \ leqslant f (n) \ leqslant c_ {2} .g (n)$ для всех достаточно больших значений n . Здесь n — положительное целое число.

Это означает, что функция g является точной оценкой для функции f .

пример

Рассмотрим данную функцию: $f (n) = 4.n ^ 3 + 10.n ^ 2 + 5.n + 1$

Учитывая $g (n) = n ^ 3$, $4.g (n) \ leqslant f (n) \ leqslant 5.g (n)$ для всех больших значений n .

Следовательно, сложность функции f (n) может быть представлена ​​в виде $\ theta (g (n))$, то есть $\ theta (n ^ 3)$.

O — обозначение

Асимптотическая верхняя граница, обеспечиваемая O-обозначением, может быть или не быть асимптотически жесткой. Оценка $2.n ^ 2 = O (n ^ 2)$ асимптотически тесная, а оценка $2.n = O (n ^ 2)$ — нет.

Мы используем o-обозначение для обозначения верхней границы, которая не является асимптотически жесткой.

Мы формально определяем o (g (n)) (little-oh of g of n) как множество f (n) = o (g (n)) для любой положительной константы $c&amp;gt; 0$, и существует значение $n_ {0}&amp;gt; 0$, так что $0 \ leqslant f (n) \ leqslant cg (n)$.

Интуитивно понятно, что в o-записи функция f (n) становится незначительной относительно g (n) при приближении n к бесконечности; то есть,

$$\ lim_ {n \ rightarrow \ infty} \ left (\ frac {f (n)} {g (n)} \ right) = 0$$

пример

Рассмотрим ту же функцию: $f (n) = 4.n ^ 3 + 10.n ^ 2 + 5.n + 1$.

Учитывая $g (n) = n ^ {4}$,

$$\ lim_ {n \ rightarrow \ infty} \ left (\ frac {4.n ^ 3 + 10.n ^ 2 + 5.n + 1} {n ^ 4} \ right) = 0$$

Следовательно, сложность функции f (n) может быть представлена ​​в виде $o (g (n))$, то есть $o (n ^ 4)$.

ω — обозначение

Мы используем ω-обозначение для обозначения нижней границы, которая не является асимптотически жесткой. Формально, однако, мы определяем ω (g (n)) (мало омега g из n) как множество f (n) = ω (g (n)) для любой положительной константы C> 0 и существует значение $n_ {0}&amp;gt; 0$, так что $0 \ leqslant cg (n) &amp;lt;f (n)$.

Например, $\ frac {n ^ 2} {2} = \ omega (n)$, но $\ frac {n ^ 2} {2} \ neq \ omega (n ^ 2)$. Соотношение $f (n) = \ omega (g (n))$ подразумевает, что существует следующий предел

$$\ lim_ {n \ rightarrow \ infty} \ left (\ frac {f (n)} {g (n)} \ right) = \ infty$$

То есть, f (n) становится произвольно большим относительно g (n), когда n приближается к бесконечности.

пример

Рассмотрим ту же функцию: $f (n) = 4.n ^ 3 + 10.n ^ 2 + 5.n + 1$

Учитывая $g (n) = n ^ 2$,

$$\ lim_ {n \ rightarrow \ infty} \ left (\ frac {4.n ^ 3 + 10.n ^ 2 + 5.n + 1} {n ^ 2} \ right) = \ infty$$

Следовательно, сложность функции f (n) может быть представлена ​​в виде $o (g (n))$, то есть $\ omega (n ^ 2)$.

Априори и Апостиари Анализ

Априорный анализ означает, что анализ выполняется до запуска его в конкретной системе. Этот анализ является этапом, когда функция определяется с использованием некоторой теоретической модели. Следовательно, мы определяем временную и пространственную сложность алгоритма, просто взглянув на алгоритм, а не на его запуск в конкретной системе с другой памятью, процессором и компилятором.

Апостиарный анализ алгоритма означает, что мы выполняем анализ алгоритма только после запуска его в системе. Это напрямую зависит от системы и меняется от системы к системе.

В отрасли мы не можем выполнить анализ Apostiari, поскольку программное обеспечение, как правило, предназначено для анонимного пользователя, который запускает его в системе, отличной от существующих в отрасли.

В Apriori это причина, по которой мы используем асимптотические нотации для определения сложности времени и пространства при их изменении с компьютера на компьютер; однако асимптотически они одинаковы.

DAA — космические сложности

В этой главе мы обсудим сложность вычислительных задач с точки зрения количества места, которое требует алгоритм.

Пространственная сложность имеет много общих черт временной сложности и служит еще одним способом классификации задач в соответствии с их вычислительными сложностями.

Что такое космическая сложность?

Пространственная сложность — это функция, описывающая объем памяти (пространства), который занимает алгоритм с точки зрения количества входных данных для алгоритма.

Мы часто говорим о дополнительной памяти , не считая памяти, необходимой для хранения самого ввода. Опять же, мы используем натуральные (но фиксированной длины) единицы измерения для этого.

Мы можем использовать байты, но проще использовать, скажем, число используемых целых чисел, количество структур фиксированного размера и т. Д.

В конце концов, функция, которую мы придумаем, не будет зависеть от фактического количества байтов, необходимых для представления единицы.

Сложность пространства иногда игнорируется, потому что используемое пространство минимально и / или очевидно, однако иногда это становится такой же важной проблемой, как сложность времени

Определение

Пусть M будет детерминированной машиной Тьюринга (TM), которая останавливается на всех входах. Пространственная сложность M — это функция $f \ colon N \ rightarrow N$, где f (n) — максимальное количество ячеек ленты, а M сканирует любой ввод длины M. Если пространственная сложность M равна f (n) , мы можем сказать, что M работает в пространстве f (n) .

Мы оцениваем пространственную сложность машины Тьюринга, используя асимптотические обозначения.

Пусть $f \ colon N \ rightarrow R ^ +$ — функция. Классы сложности пространства могут быть определены следующим образом:

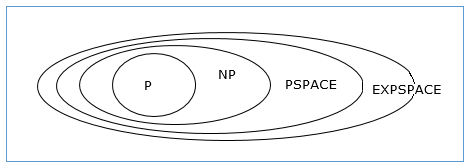
ПРОСТРАНСТВО = {L | L — это язык, определяемый O (f (n)) пространственным детерминистом TM}

ПРОСТРАНСТВО = {L | L — это язык, определяемый недетерминированным TM пространства O (f (n))}

PSPACE — это класс языков, разрешимых в полиномиальном пространстве на детерминированной машине Тьюринга.

Другими словами, PSPACE = U _k SPACE (n ^k )

Теорема Савича

Одной из самых ранних теорем, связанных со сложностью пространства, является теорема Савича. Согласно этой теореме, детерминированная машина может моделировать недетерминированные машины, используя небольшое количество пространства.

Для сложности времени такое моделирование требует экспоненциального увеличения времени. Для сложности пространства эта теорема показывает, что любая недетерминированная машина Тьюринга, которая использует пространство f (n), может быть преобразована в детерминированную ТМ, которая использует пространство f ² (n) .

Следовательно, теорема Савича утверждает, что для любой функции $f \ colon N \ rightarrow R ^ +$, где $f (n) \ geqslant n$

NSPACE (f (n)) ⊆ SPACE (f (n))

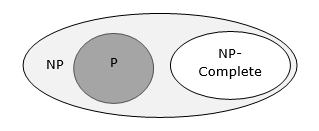
Отношения между классами сложности

Следующая диаграмма изображает отношения между различными классами сложности.

До сих пор мы не обсуждали классы P и NP в этом уроке. Это будет обсуждаться позже.

DAA — разделяй и властвуй

Многие алгоритмы по своей природе являются рекурсивными для решения данной проблемы, рекурсивно решая подзадачи.

При подходе «разделяй и властвуй» проблема делится на более мелкие проблемы, затем меньшие проблемы решаются независимо, и, наконец, решения небольших проблем объединяются в решение большой проблемы.

Как правило, алгоритмы «разделяй и властвуй» состоят из трех частей:

• Разделите проблему на несколько подзадач, которые являются небольшими экземплярами одной и той же проблемы.

• Покорите подзадачи , решая их рекурсивно. Если они достаточно малы, решите подзадачи как базовые.

• Объедините решения подзадач в решение исходной задачи.

Разделите проблему на несколько подзадач, которые являются небольшими экземплярами одной и той же проблемы.

Покорите подзадачи , решая их рекурсивно. Если они достаточно малы, решите подзадачи как базовые.

Объедините решения подзадач в решение исходной задачи.

Плюсы и минусы подхода «разделяй и властвуй»

Подход «разделяй и властвуй» поддерживает параллелизм, поскольку подзадачи независимы. Следовательно, алгоритм, который разработан с использованием этого метода, может работать в многопроцессорной системе или на разных машинах одновременно.

При таком подходе большинство алгоритмов разрабатываются с использованием рекурсии, поэтому управление памятью очень высоко. Для рекурсивной функции используется стек, где необходимо сохранить состояние функции.

Применение подхода «разделяй и властвуй»

Ниже приведены некоторые проблемы, которые решаются с использованием подхода «разделяй и властвуй».

• Нахождение максимума и минимума последовательности чисел
• Матричное умножение Штрассена
• Сортировка слиянием
• Бинарный поиск

DAA — проблема Макс-Мин

Рассмотрим простую проблему, которая может быть решена с помощью техники «разделяй и властвуй».

Постановка задачи

Задача Макс-Мин в анализе алгоритма — найти максимальное и минимальное значение в массиве.

Решение

Чтобы найти максимальное и минимальное число в данном массиве номеров [] размера n , можно использовать следующий алгоритм. Сначала мы представляем наивный метод, а затем представим подход «разделяй и властвуй» .

Наивный метод

Наивный метод является основным методом решения любой проблемы. В этом методе максимальное и минимальное количество можно найти отдельно. Чтобы найти максимальное и минимальное число, можно использовать следующий простой алгоритм.

Algorithm: Max-Min-Element (numbers[]) 
max := numbers[1] 
min := numbers[1] 

for i = 2 to n do 
   if numbers[i] > max then  
      max := numbers[i] 
   if numbers[i] < min then  
      min := numbers[i] 
return (max, min) 

Анализ

Количество сравнений в наивном методе составляет 2n — 2 .

Количество сравнений можно уменьшить, используя подход «разделяй и властвуй». Ниже приводится методика.

Разделяй и властвуй

При таком подходе массив делится на две половины. Затем с помощью рекурсивного подхода определяются максимальные и минимальные числа в каждой половине. Позже верните максимум двух максимумов каждой половины и минимум двух минимумов каждой половины.

В данной задаче число элементов в массиве равно $y - x + 1$, где y больше или равно x .

$\ mathbf {\ mathit {Max - Min (x, y)}}$ вернет максимальное и минимальное значения массива $\ mathbf {\ mathit {numbers [x ... y]}}$.

Algorithm: Max - Min(x, y) 
if y – x ≤ 1 then  
   return (max(numbers[x], numbers[y]), min((numbers[x], numbers[y])) 
else 
   (max1, min1):= maxmin(x, ⌊((x + y)/2)⌋) 
   (max2, min2):= maxmin(⌊((x + y)/2) + 1)⌋,y) 
return (max(max1, max2), min(min1, min2)) 

Анализ

Пусть T (n) будет числом сравнений, сделанных $\ mathbf {\ mathit {Max - Min (x, y)}}$, где количество элементов $n = y - x + 1$.

Если T (n) представляет числа, то отношение повторения может быть представлено как

$$T (n) = \ begin {case} T \ left (\ lfloor \ frac {n} {2} \ rfloor \ right) + T \ left (\ lceil \ frac {n} {2} \ rceil \ right ) +2 &amp;amp; для \: n&amp;gt; 2 \\ 1 &amp;amp; для \: n = 2 \\ 0 &amp;amp; для \: n = 1 \ end {case}$$

Предположим, что n имеет вид степени 2 . Следовательно, n = 2 ^k, где k — высота дерева рекурсии.

Так,

$$T (n) = 2.T (\ frac {n} {2}) + 2 = 2. \ left (\ begin {array} {c} 2.T (\ frac {n} {4}) + 2 \ end {array} \ right) + 2 ..... = \ frac {3n} {2} - 2$$

По сравнению с наивным методом, в подходе «разделяй и властвуй», количество сравнений меньше. Однако, используя асимптотические обозначения, оба подхода представлены O (n) .

DAA — сортировка слиянием

В этой главе мы обсудим сортировку слиянием и проанализируем ее сложность.

Постановка задачи

Проблема сортировки списка чисел сразу поддается стратегии «разделяй и властвуй»: разбейте список на две половины, рекурсивно сортируйте каждую половину, а затем объедините два отсортированных подсписка.

Решение

В этом алгоритме числа хранятся в массиве numbers [] . Здесь p и q представляют начальный и конечный индексы подмассива.

Algorithm: Merge-Sort (numbers[], p, r) 
if p < r then  
q = ⌊(p + r) / 2⌋ 
Merge-Sort (numbers[], p, q) 
    Merge-Sort (numbers[], q + 1, r) 
    Merge (numbers[], p, q, r) 

Function: Merge (numbers[], p, q, r)
n 1 = q – p + 1 
n 2 = r – q 
declare leftnums[1…n 1 + 1] and rightnums[1…n 2 + 1] temporary arrays 
for i = 1 to n 1 
   leftnums[i] = numbers[p + i - 1] 
for j = 1 to n 2 
   rightnums[j] = numbers[q+ j] 
leftnums[n 1 + 1] = ∞ 
rightnums[n 2 + 1] = ∞ 
i = 1 
j = 1 
for k = p to r 
   if leftnums[i] ≤ rightnums[j] 
      numbers[k] = leftnums[i] 
      i = i + 1 
   else
      numbers[k] = rightnums[j] 
      j = j + 1 

Анализ

Рассмотрим время выполнения Merge-Sort как T (n) . Следовательно,

$T (n) = \ begin {case} c &amp;amp; if \: n \ leqslant 1 \\ 2 \: x \: T (\ frac {n} {2}) + d \: x \: n &amp;amp; в противном случае \ end {case}$, где c и d — константы

Следовательно, используя это рекуррентное соотношение,

$$T (n) = 2 ^ i T (\ frac {n} {2 ^ i}) + idn$$

As, $i = log \: n, \: T (n) = 2 ^ {log \: n} T (\ frac {n} {2 ^ {log \: n}}) + log \: ndn$

$= \: cn + dnlog \: n$

Следовательно, $T (n) = O (n \: log \: n)$

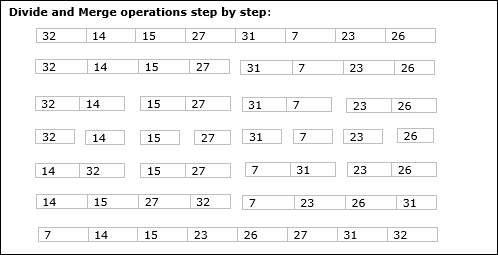
пример

В следующем примере мы продемонстрировали алгоритм Merge-Sort шаг за шагом. Во-первых, каждый итерационный массив делится на два вложенных массива, пока этот массив не содержит только один элемент. Когда эти подмассивы не могут быть разделены далее, выполняются операции слияния.

DAA — бинарный поиск

В этой главе мы обсудим другой алгоритм, основанный на методе «разделяй и властвуй».

Постановка задачи

Двоичный поиск может быть выполнен по отсортированному массиву. В этом подходе индекс элемента x определяется, если элемент принадлежит списку элементов. Если массив не отсортирован, для определения позиции используется линейный поиск.

Решение

В этом алгоритме мы хотим выяснить, принадлежит ли элемент x к набору чисел, хранящихся в массиве numbers [] . Где l и r представляют левый и правый индекс подмассива, в котором должна выполняться операция поиска.

Algorithm: Binary-Search(numbers[], x, l, r)
if l = r then  
   return l  
else 
   m := ⌊(l + r) / 2⌋ 
   if x ≤ numbers[m]  then 
      return Binary-Search(numbers[], x, l, m) 
   else 
      return Binary-Search(numbers[], x, m+1, r) 

Анализ

Линейный поиск выполняется за O (n) раз. В то время как бинарный поиск выдает результат за O (log n)

Пусть T (n) будет количеством сравнений в худшем случае в массиве из n элементов.

Следовательно,

$$T (n) = \ begin {case} 0 &amp;amp; if \: n = 1 \\ T (\ frac {n} {2}) + 1 &amp;amp; в противном случае \ end {case}$$

Используя это рекуррентное соотношение $T (n) = log \: n$.

Следовательно, бинарный поиск использует $O (log \: n)$ time.

пример

В этом примере мы собираемся найти элемент 63.

DAA — матричное умножение Штрассена

В этой главе сначала мы обсудим общий метод умножения матриц, а позже мы обсудим алгоритм умножения матриц Штрассена.

Постановка задачи

Рассмотрим две матрицы X и Y. Мы хотим вычислить результирующую матрицу Z , умножив X и Y.

Наивный метод

Сначала обсудим наивный метод и его сложность. Здесь мы вычисляем Z = X × Y. Используя наивный метод, две матрицы ( X и Y ) могут быть умножены, если порядок этих матриц p × q и q × r . Ниже приводится алгоритм.

Algorithm: Matrix-Multiplication (X, Y, Z) 
for i = 1 to p do 
   for j = 1 to r do 
      Z[i,j] := 0 
      for k = 1 to q do 
         Z[i,j] := Z[i,j] + X[i,k] × Y[k,j] 

сложность

Здесь мы предполагаем, что целочисленные операции занимают O (1) времени. В этом алгоритме есть три цикла for, и один вложен в другой. Следовательно, алгоритм занимает O (n ³ ) времени для выполнения.

Алгоритм умножения матриц Штрассена

В этом контексте, используя алгоритм умножения матриц Штрассена, можно немного улучшить потребление времени.

Умножение матрицы Штрассена может быть выполнено только на квадратных матрицах, где n — степень 2 . Порядок обеих матриц n × n .

Разделите X , Y и Z на четыре (n / 2) × (n / 2) матрицы, как показано ниже —

$Z = \ begin {bmatrix} I &amp;amp; J \\ K &amp;amp; L \ end {bmatrix}$ $X = \ begin {bmatrix} A &amp;amp; B \\ C &amp;amp; D \ end {bmatrix}$ и $Y = \ begin {bmatrix} E &amp;amp; F \\ G &amp;amp; H \ end {bmatrix}$

Используя алгоритм Штрассена, вычислите следующее:

$$M_ {1} \: \ colon = (A + C) \ times (E + F)$$

$$M_ {2} \: \ colon = (B + D) \ times (G + H)$$

$$M_ {3} \: \ colon = (AD) \ times (E + H)$$

$$M_ {4} \: \ colon = A \ times (FH)$$

$$M_ {5} \: \ colon = (C + D) \ times (E)$$

$$M_ {6} \: \ colon = (A + B) \ times (H)$$

$$M_ {7} \: \ colon = D \ times (GE)$$

Затем,

$$I \: \ colon = M_ {2} + M_ {3} - M_ {6} - M_ {7}$$

$$J \: \ colon = M_ {4} + M_ {6}$$

$$K \: \ colon = M_ {5} + M_ {7}$$

$$L \: \ colon = M_ {1} - M_ {3} - M_ {4} - M_ {5}$$

Анализ

$T (n) = \ begin {case} c &amp;amp; if \: n = 1 \\ 7 \: x \: T (\ frac {n} {2}) + d \: x \: n ^ 2 &amp;amp; в противном случае \ end {case}$, где c и d — константы

Используя это рекуррентное соотношение, мы получаем $T (n) = O (n ^ {log7})$

Следовательно, сложность алгоритма умножения матриц Штрассена составляет $O (n ^ {log7})$.

DAA — Жадный метод

Среди всех алгоритмических подходов наиболее простым и понятным является метод Жадности. При таком подходе решение принимается на основе текущей доступной информации, не беспокоясь о влиянии текущего решения в будущем.

Жадные алгоритмы строят решение по частям, выбирая следующую часть таким образом, чтобы она сразу приносила пользу. Этот подход никогда не пересматривает выбор, принятый ранее. Этот подход в основном используется для решения задач оптимизации. Жадный метод прост в реализации и достаточно эффективен в большинстве случаев. Следовательно, мы можем сказать, что алгоритм Greedy — это алгоритмическая парадигма, основанная на эвристике, которая следует за локальным оптимальным выбором на каждом шаге в надежде найти глобальное оптимальное решение.

Во многих задачах оно не дает оптимального решения, хотя и дает приблизительное (почти оптимальное) решение за разумное время.

Компоненты жадного алгоритма

Жадные алгоритмы имеют следующие пять компонентов —

• Набор кандидатов — решение создано из этого набора.

• Функция выбора — используется для выбора лучшего кандидата для добавления в решение.

• ТЭО — используется для определения того, можно ли использовать кандидата для внесения вклада в решение.

• Целевая функция — используется для присвоения значения решению или частичному решению.

• Функция решения — используется, чтобы указать, было ли достигнуто полное решение.

Набор кандидатов — решение создано из этого набора.

Функция выбора — используется для выбора лучшего кандидата для добавления в решение.

ТЭО — используется для определения того, можно ли использовать кандидата для внесения вклада в решение.

Целевая функция — используется для присвоения значения решению или частичному решению.

Функция решения — используется, чтобы указать, было ли достигнуто полное решение.

Области применения

Жадный подход используется для решения многих проблем, таких как

• Нахождение кратчайшего пути между двумя вершинами с использованием алгоритма Дейкстры.

• Нахождение минимального остовного дерева в графе с использованием алгоритма Прима / Крускала и т. Д.

Нахождение кратчайшего пути между двумя вершинами с использованием алгоритма Дейкстры.

Нахождение минимального остовного дерева в графе с использованием алгоритма Прима / Крускала и т. Д.

Там, где терпит неудачу жадный подход

Во многих задачах алгоритм Жадного не может найти оптимальное решение, более того, он может привести к худшему решению. Такие проблемы, как Traveling Salesman и Knapsack, не могут быть решены с помощью этого подхода.

DAA — Фракционный рюкзак

Алгоритм Жадности может быть очень хорошо понят с хорошо известной проблемой, называемой проблемой ранца. Хотя та же проблема может быть решена путем использования других алгоритмических подходов, подход Greedy позволяет решить проблему дробного ранца в разумные сроки. Остановимся подробнее на проблеме рюкзака.

Рюкзак Проблема

По заданному набору предметов, каждый из которых имеет вес и значение, определяют поднабор предметов для включения в коллекцию, чтобы общий вес был меньше или равен заданному пределу, а общее значение было как можно большим.

Задача о ранце лежит в задаче комбинаторной оптимизации. Он появляется как подзадача во многих более сложных математических моделях реальных проблем. Один общий подход к сложным задачам состоит в том, чтобы определить наиболее ограничивающее ограничение, игнорировать другие, решить проблему ранца и каким-то образом скорректировать решение, чтобы удовлетворить игнорируемым ограничениям.

Приложения

Во многих случаях выделения ресурсов наряду с некоторыми ограничениями, проблема может быть выведена аналогичным образом, как и в случае с ранцем. Ниже приведен набор примеров.

• Нахождение наименее расточительного способа резки сырья
• оптимизация портфеля
• Проблемы с заготовкой

Сценарий проблемы

Вор грабит магазин и может нести максимальный вес W в свой рюкзак. В магазине доступно n предметов, и вес i- ^го предмета равен w _i, а его прибыль равна p _i . Какие вещи должен взять вор?

В этом контексте предметы должны быть выбраны таким образом, что вор будет нести те предметы, за которые он получит максимальную прибыль. Следовательно, цель вора — максимизировать прибыль.

В зависимости от характера предметов проблемы с рюкзаком подразделяются на

• Фракционный рюкзак
• ранец

Фракционный рюкзак

В этом случае предметы могут быть разбиты на более мелкие кусочки, поэтому вор может выбирать фракции предметов.

Согласно постановке задачи,

• В магазине n товаров

• Вес i- ^го предмета $w_ {i}&amp;gt; 0$

• Прибыль за i- ^й товар $p_ {i}&amp;gt; 0$ и

• Емкость Рюкзака Вт

В магазине n товаров

Вес i- ^го предмета $w_ {i}&amp;gt; 0$

Прибыль за i- ^й товар $p_ {i}&amp;gt; 0$ и

Емкость Рюкзака Вт

В этой версии задачи о ранце предметы могут быть разбиты на более мелкие части. Таким образом, вор может взять только часть x _i из i- ^го предмета.

$$0 \ leqslant x_ {i} \ leqslant 1$$

I- ^й элемент добавляет вес $x_ {i} .w_ {i}$ к общему весу в рюкзаке, а прибыль $x_ {i} .p_ {i}$ — к общей прибыли.

Следовательно, целью этого алгоритма является

$$maximize \: \ displaystyle \ sum \ limit_ {n = 1} ^ n (x_ {i} .p _ {} i)$$

с учетом ограничений,

$$\ displaystyle \ sum \ limit_ {n = 1} ^ n (x_ {i} .w _ {} i) \ leqslant W$$

Понятно, что оптимальное решение должно точно заполнять рюкзак, иначе мы могли бы добавить дробь одного из оставшихся предметов и увеличить общую прибыль.

Таким образом, оптимальное решение может быть получено

$$\ displaystyle \ sum \ limit_ {n = 1} ^ n (x_ {i} .w _ {} i) = W$$

В этом контексте сначала нам нужно отсортировать эти элементы по значению $\ frac {p_ {i}} {w_ {i}}$, так что $\ frac {p_ {i} +1} {w_ {i } +1}$ ≤ $\ frac {p_ {i}} {w_ {i}}$. Здесь x — массив для хранения доли элементов.

Algorithm: Greedy-Fractional-Knapsack (w[1..n], p[1..n], W) 
for i = 1 to n 
   do x[i] = 0 
weight = 0 
for i = 1 to n 
   if weight + w[i] ≤ W then  
      x[i] = 1 
      weight = weight + w[i] 
   else 
      x[i] = (W - weight) / w[i] 
      weight = W 
      break 
return x

Анализ

Если предоставленные элементы уже отсортированы в порядке убывания $\ mathbf {\ frac {p_ {i}} {w_ {i}}}$, тогда цикл while занимает время в O (n) ; Следовательно, общее время, включая сортировку, составляет O (n logn) .

пример

Предположим, что вместимость ранца W = 60 и список предоставленных предметов показаны в следующей таблице:

Вещь		В	С	D
прибыль	280	100	120	120
Вес	40	10	20	24
Соотношение $(\ frac {p_ {i}} {w_ {i}})$	7	10	6	5

Поскольку предоставленные элементы не отсортированы на основе $\ mathbf {\ frac {p_ {i}} {w_ {i}}}$. После сортировки элементы отображаются так, как показано в следующей таблице.

Вещь	В		С	D
прибыль	100	280	120	120
Вес	10	40	20	24
Соотношение $(\ frac {p_ {i}} {w_ {i}})$	10	7	6	5

Решение

После сортировки всех элементов по $\ frac {p_ {i}} {w_ {i}}$. Сначала выбирается все B, так как вес B меньше вместимости рюкзака. Затем выбирается элемент A , так как доступная вместимость рюкзака больше, чем вес A. Теперь C выбран в качестве следующего элемента. Тем не менее, весь предмет не может быть выбран, так как оставшийся объем рюкзака меньше, чем вес C.

Следовательно, доля C (то есть (60 — 50) / 20) выбрана.

Теперь вместимость рюкзака равна выбранным предметам. Следовательно, больше ничего нельзя выбрать.

Общий вес выбранных предметов составляет 10 + 40 + 20 * (10/20) = 60

И общая прибыль составляет 100 + 280 + 120 * (10/20) = 380 + 60 = 440

Это оптимальное решение. Мы не можем получить больше прибыли, выбирая любую другую комбинацию предметов.

DAA — последовательность работ с крайним сроком

Постановка задачи

Задача определения последовательности заданий состоит в том, чтобы найти последовательность заданий, которая выполняется в установленные сроки и дает максимальную прибыль.

Решение

Давайте рассмотрим, набор из n заданных заданий, которые связаны со сроками и прибыль получается, если задание завершено к его крайнему сроку. Эти рабочие места должны быть заказаны таким образом, чтобы была максимальная прибыль.

Может случиться так, что все данные задания не будут выполнены в установленные сроки.

Предположим, срок выполнения i- ^го задания J _i — d _i, а прибыль, полученная от этого задания, — p _i . Следовательно, оптимальное решение этого алгоритма является возможным решением с максимальной прибылью.

Таким образом, $D (i)&amp;gt; 0$ для $1 \ leqslant i \ leqslant n$.

Первоначально эти задания упорядочены в соответствии с прибылью, т.е. $p_ {1} \ geqslant p_ {2} \ geqslant p_ {3} \ geqslant \: ... \: \ geqslant p_ {n}$.

Algorithm: Job-Sequencing-With-Deadline (D, J, n, k) 
D(0) := J(0) := 0 
k := 1 
J(1) := 1   // means first job is selected 
for i = 2 … n do 
   r := k 
   while D(J(r)) > D(i) and D(J(r)) ≠ r do 
      r := r – 1 
   if D(J(r)) ≤ D(i) and D(i) > r then 
      for l = k … r + 1 by -1 do 
         J(l + 1) := J(l) 
         J(r + 1) := i 
         k := k + 1 

Анализ

В этом алгоритме мы используем два цикла, один внутри другого. Следовательно, сложность этого алгоритма составляет $O (n ^ 2)$.

пример

Давайте рассмотрим набор заданий, как показано в следующей таблице. Мы должны найти последовательность заданий, которые будут выполнены в установленные сроки и принесут максимальную прибыль. Каждая работа связана со сроками и прибылью.

работа	J 1	J 2	J 3	J 4	J 5
Крайний срок	2	1	3	2	1
прибыль	60	100	20	40	20

Решение

Чтобы решить эту проблему, данные работы сортируются в соответствии с их прибылью в порядке убывания. Следовательно, после сортировки задания упорядочиваются, как показано в следующей таблице.

работа	J 2	J 1	J 4	J 3	J 5
Крайний срок	1	2	2	3	1
прибыль	100	60	40	20	20

Из этого набора заданий сначала выбираем J ₂ , так как он может быть выполнен в установленные сроки и приносит максимальную прибыль.

• Затем выбирается J _1, поскольку он дает больше прибыли по сравнению с J ₄ .

• На следующих часах J ₄ не может быть выбран, поскольку его крайний срок истек, поэтому J ₃ выбирается, поскольку он выполняется в пределах своего крайнего срока.

• Задание J ₅ отбрасывается, поскольку оно не может быть выполнено в срок.

Затем выбирается J _1, поскольку он дает больше прибыли по сравнению с J ₄ .

На следующих часах J ₄ не может быть выбран, поскольку его крайний срок истек, поэтому J ₃ выбирается, поскольку он выполняется в пределах своего крайнего срока.

Задание J ₅ отбрасывается, поскольку оно не может быть выполнено в срок.

Таким образом, решение — это последовательность заданий ( J ₂ , J ₁ , J ₃ ), которые выполняются в установленные сроки и дают максимальную прибыль.

Общая прибыль этой последовательности составляет 100 + 60 + 20 = 180 .

DAA — оптимальный шаблон слияния

Объедините набор отсортированных файлов разной длины в один отсортированный файл. Нам нужно найти оптимальное решение, где результирующий файл будет сгенерирован за минимальное время.

Если указано количество отсортированных файлов, существует много способов объединить их в один отсортированный файл. Это слияние может быть выполнено парами. Следовательно, этот тип слияния называется двухсторонними шаблонами слияния .

Поскольку разные пары требуют разного количества времени, в этой стратегии мы хотим определить оптимальный способ объединения множества файлов. На каждом шаге объединяются две самые короткие последовательности.

Чтобы объединить файл p-записи и файл q-записи, возможно, потребуется перемещение записей p + q , очевидный выбор которого заключается в объединении двух самых маленьких файлов вместе на каждом шаге.

Шаблоны двустороннего слияния могут быть представлены двоичными деревьями слияния. Рассмотрим набор из n отсортированных файлов {f ₁ , f ₂ , f ₃ ,…, f _n } . Первоначально каждый элемент этого рассматривается как двоичное дерево одного узла. Чтобы найти это оптимальное решение, используется следующий алгоритм.

Algorithm: TREE (n)  
for i := 1 to n – 1 do  
   declare new node  
   node.leftchild := least (list) 
   node.rightchild := least (list) 
   node.weight) := ((node.leftchild).weight) + ((node.rightchild).weight)  
   insert (list, node);  
return least (list); 

В конце этого алгоритма вес корневого узла представляет собой оптимальную стоимость.

пример

Рассмотрим данные файлы, f ₁ , f ₂ , f ₃ , f ₄ и f ₅ с 20, 30, 10, 5 и 30 количеством элементов соответственно.

Если операции слияния выполняются в соответствии с предоставленной последовательностью, то

M ₁ = объединить f ₁ и f ₂ => 20 + 30 = 50

M ₂ = объединить M ₁ и f ₃ => 50 + 10 = 60

М ₃ = объединить М ₂ и f ₄ => 60 + 5 = 65

М ₄ = объединить М ₃ и f ₅ => 65 + 30 = 95

Следовательно, общее количество операций

50 + 60 + 65 + 95 = 270

Теперь возникает вопрос, есть ли лучшее решение?

Сортируя числа по размеру в порядке возрастания, получаем следующую последовательность:

f ₄ , f ₃ , f ₁ , f ₂ , f ₅

Следовательно, операции слияния могут быть выполнены на этой последовательности

M ₁ = объединить f ₄ и f ₃ => 5 + 10 = 15

M ₂ = объединить M ₁ и f ₁ => 15 + 20 = 35

М ₃ = объединить М ₂ и f ₂ => 35 + 30 = 65

М ₄ = объединить М ₃ и f ₅ => 65 + 30 = 95

Следовательно, общее количество операций

15 + 35 + 65 + 95 = 210

Очевидно, это лучше, чем предыдущий.

В этом контексте мы сейчас собираемся решить проблему, используя этот алгоритм.

Начальный набор

Шаг 1

Шаг 2

Шаг 3

Шаг 4

Следовательно, решение занимает 15 + 35 + 60 + 95 = 205 количество сравнений.

DAA — динамическое программирование

Динамическое программирование также используется в задачах оптимизации. Как и метод «разделяй и властвуй», динамическое программирование решает проблемы путем объединения решений подзадач. Более того, алгоритм динамического программирования решает каждую подзадачу только один раз, а затем сохраняет свой ответ в таблице, тем самым избегая повторного вычисления ответа каждый раз.

Два основных свойства проблемы предполагают, что данная проблема может быть решена с помощью динамического программирования. Эти свойства являются перекрывающимися подзадачами и оптимальной подструктурой .

Перекрывающиеся подзадачи

Подобно подходу «разделяй и властвуй», динамическое программирование также сочетает в себе решения подзадач. Он в основном используется там, где решение одной подзадачи необходимо повторно. Вычисленные решения хранятся в таблице, поэтому их не нужно пересчитывать. Следовательно, этот метод необходим там, где существует перекрывающаяся подзадача.

Например, бинарный поиск не имеет перекрывающейся подзадачи. В то время как рекурсивная программа чисел Фибоначчи имеет много перекрывающихся подзадач.

Оптимальная подструктура

Данная задача имеет свойство оптимальной подструктуры, если оптимальное решение данной задачи может быть получено с использованием оптимальных решений ее подзадач.

Например, задача Кратчайшего пути имеет следующее оптимальное свойство подструктуры —

Если узел x лежит в кратчайшем пути от исходного узла u к узлу назначения v , то кратчайший путь от u до v является комбинацией кратчайшего пути от u до x и кратчайшего пути от x до v .

Стандартные алгоритмы All Pair Shortest Path, такие как Floyd-Warshall и Bellman-Ford, являются типичными примерами динамического программирования.

Шаги подхода динамического программирования

Алгоритм динамического программирования разработан с использованием следующих четырех шагов —

• Охарактеризуйте структуру оптимального решения.
• Рекурсивно определить значение оптимального решения.
• Вычислить значение оптимального решения, как правило, восходящим способом.
• Построить оптимальное решение из вычисленной информации.

Применение подхода динамического программирования

• Матричное умножение
• Самая длинная общая подпоследовательность
• Задача коммивояжера

DAA — Рюкзак 0-1

В этом уроке ранее мы обсуждали проблему дробного ранца с использованием подхода Greedy. Мы показали, что подход Гриди дает оптимальное решение для дробного ранца. Тем не менее, эта глава рассмотрит проблему ранца 0-1 и ее анализ.

В 0-1 ранце предметы не могут быть разбиты, что означает, что вор должен взять предмет целиком или оставить его. Это причина называть его 0-1 рюкзаком.

Следовательно, в случае 0-1 ранца значение x _i может быть либо 0, либо 1 , где другие ограничения остаются прежними.

0-1 Рюкзак не может быть решен жадным подходом. Жадный подход не гарантирует оптимального решения. Во многих случаях жадный подход может дать оптимальное решение.

Следующие примеры установят наше утверждение.

Пример-1

Давайте рассмотрим, что вместимость рюкзака составляет W = 25, а предметы соответствуют показанным в следующей таблице.

Вещь		В	С	D
прибыль	24	18	18	10
Вес	24	10	10	7

Без учета прибыли на единицу веса ( p _i / w _i ), если мы применим подход Greedy для решения этой проблемы, будет выбран первый элемент A , так как он принесет максимальную прибыль среди всех элементов.

После выбора элемента A больше не будет выбран. Следовательно, для данного набора предметов общая прибыль составляет 24 . Принимая во внимание, что оптимальное решение может быть достигнуто путем выбора предметов, B и C, где общая прибыль составляет 18 + 18 = 36.

Пример-2

Вместо выбора элементов на основе общего преимущества, в этом примере элементы выбираются на основе отношения p _i / w _i . Давайте рассмотрим, что вместимость рюкзака составляет W = 60, и предметы, как показано в следующей таблице.

Вещь		В	С
Цена	100	280	120
Вес	10	40	20
соотношение	10	7	6

Используя жадный подход, выбирается первый элемент А. Затем выбирается следующий элемент B. Следовательно, общая прибыль составляет 100 + 280 = 380 . Тем не менее, оптимальное решение этого случая может быть достигнуто путем выбора пунктов B и C , где общая прибыль составляет 280 + 120 = 400 .

Следовательно, можно сделать вывод, что жадный подход может не дать оптимального решения.

Для решения 0-1 ранца требуется подход динамического программирования.

Постановка задачи

Вор грабит магазин и может нести максимальный вес W в свой рюкзак. Есть n предметов, и вес i- ^го предмета равен w _i, а прибыль от выбора этого предмета равна p _i . Какие вещи должен взять вор?

Динамически-программный подход

Пусть я будет номером с наибольшим номером в оптимальном решении S для W долларов. Тогда S ^‘ = S — {i} является оптимальным решением для W — w _i долларов, а значение решения S равно V _i плюс значение подзадачи.

Мы можем выразить этот факт в следующей формуле: определите c [i, w] как решение для пунктов 1,2,…, i и максимального веса w .

Алгоритм принимает следующие входные данные

• Максимальный вес мамы W

• Количество предметов n

• Две последовательности v = <v ₁ , v ₂ ,…, v _n > и w = <w ₁ , w ₂ ,…, w _n >

Максимальный вес мамы W

Количество предметов n

Две последовательности v = <v ₁ , v ₂ ,…, v _n > и w = <w ₁ , w ₂ ,…, w _n >

Dynamic-0-1-knapsack (v, w, n, W) 
for w = 0 to W do 
   c[0, w] = 0 
for i = 1 to n do 
   c[i, 0] = 0 
   for w = 1 to W do 
      if w i ≤ w then 
         if v i + c[i-1, w-w i ] then 
            c[i, w] = v i + c[i-1, w-w i ] 
         else c[i, w] = c[i-1, w] 
      else 
         c[i, w] = c[i-1, w] 

Набор элементов, которые нужно взять, может быть выведен из таблицы, начиная с c [n, w] и прослеживая назад, откуда пришли оптимальные значения.

Если c [i, w] = c [i-1, w] , то элемент i не является частью решения, и мы продолжаем трассировку с помощью c [i-1, w] . В противном случае элемент i является частью решения, и мы продолжаем трассировку с помощью c [i-1, wW] .

Анализ

Этот алгоритм занимает θ ( n , w ) раз, так как таблица c имеет ( n + 1). ( W + 1) записей, где каждая запись требует θ (1) времени для вычисления.

DAA — самая длинная общая подпоследовательность

Самая длинная общая проблема подпоследовательности — найти самую длинную последовательность, которая существует в обеих заданных строках.

подпоследовательности

Рассмотрим последовательность S = <s ₁ , s ₂ , s ₃ , s ₄ ,…, s _n >.

Последовательность Z = <z ₁ , z ₂ , z ₃ , z ₄ ,…, z _m > над S называется подпоследовательностью S, если и только если она может быть получена из удаления S некоторых элементов.

Общая подпоследовательность

Предположим, что X и Y две последовательности над конечным множеством элементов. Можно сказать, что Z является общей подпоследовательностью X и Y , если Z является подпоследовательностью как X, так и Y.

Самая длинная общая подпоследовательность

Если задан набор последовательностей, самая длинная общая проблема подпоследовательности состоит в том, чтобы найти общую подпоследовательность всех последовательностей, которая имеет максимальную длину.

Самая длинная общая проблема подпоследовательности — это классическая проблема информатики, основа программ сравнения данных, таких как diff-утилита, и применяется в биоинформатике. Он также широко используется системами контроля версий, такими как SVN и Git, для согласования нескольких изменений, внесенных в коллекцию файлов с контролем версий.

Наивный метод

Пусть X — последовательность длины m, а Y — последовательность длины n . Проверьте для каждой подпоследовательности X , является ли она подпоследовательностью Y , и верните самую длинную общую найденную подпоследовательность.

Есть 2 ^m подпоследовательностей X. Проверка последовательности, является ли она подпоследовательностью Y, занимает O (n) времени. Таким образом, наивный алгоритм занял бы O (n2 ^m ) времени.

Динамическое программирование

Пусть X = <x ₁ , x ₂ , x ₃ ,…, x _m > и Y = <y ₁ , y ₂ , y ₃ ,…, y _n > — последовательности. Для вычисления длины элемента используется следующий алгоритм.

В этой процедуре таблица C [m, n] вычисляется в главном порядке строк, а другая таблица B [m, n] вычисляется для построения оптимального решения.

Algorithm: LCS-Length-Table-Formulation (X, Y)
m := length(X) 
n := length(Y) 
for i = 1 to m do 
   C[i, 0] := 0 
for j = 1 to n do 
   C[0, j] := 0 
for i = 1 to m do 
   for j = 1 to n do 
      if x i = y j 
         C[i, j] := C[i - 1, j - 1] + 1 
         B[i, j] := ‘D’ 
      else 
         if C[i -1, j] ≥ C[i, j -1] 
            C[i, j] := C[i - 1, j] + 1 
            B[i, j] := ‘U’ 
         else 
         C[i, j] := C[i, j - 1]
         B[i, j] := ‘L’ 
return C and B

Algorithm: Print-LCS (B, X, i, j)
if i = 0 and j = 0 
   return  
if B[i, j] = ‘D’ 
   Print-LCS(B, X, i-1, j-1) 
   Print(x i ) 
else if B[i, j] = ‘U’ 
   Print-LCS(B, X, i-1, j) 
else 
   Print-LCS(B, X, i, j-1) 

Этот алгоритм выведет самую длинную общую подпоследовательность X и Y.

Анализ

Чтобы заполнить таблицу, внешний цикл for повторяется m раз, а внутренний цикл for повторяется n раз. Следовательно, сложность алгоритма составляет O (m, n) , где m и n — длина двух строк.

пример

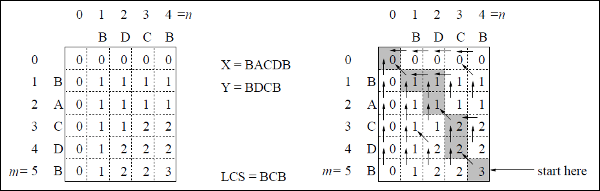
В этом примере у нас есть две строки X = BACDB и Y = BDCB, чтобы найти самую длинную общую подпоследовательность.

Следуя алгоритму LCS-Length-Table-Formulation (как указано выше), мы рассчитали таблицу C (показана слева) и таблицу B (показаны справа).

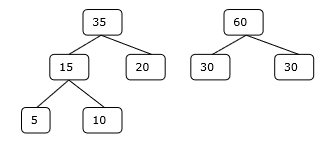
В таблице B вместо «D», «L» и «U» мы используем диагональную стрелку, стрелку влево и стрелку вверх соответственно. После генерации таблицы B LCS определяется функцией LCS-Print. Результат BCB.

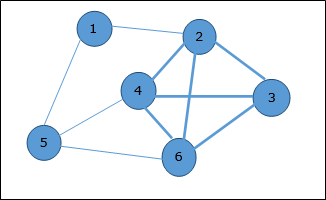
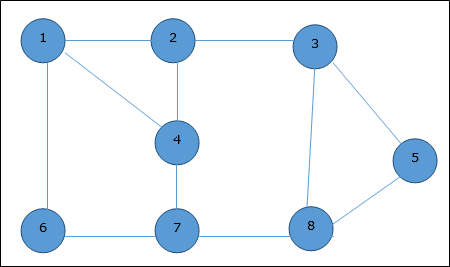
DAA — Spanning Tree

Связующее дерево — это подмножество неориентированного графа, в котором все вершины связаны минимальным числом ребер.

Если все вершины связаны в графе, то существует хотя бы одно остовное дерево. На графике может существовать более одного связующего дерева.

свойства

• У остовного дерева нет цикла.
• Любая вершина может быть достигнута из любой другой вершины.

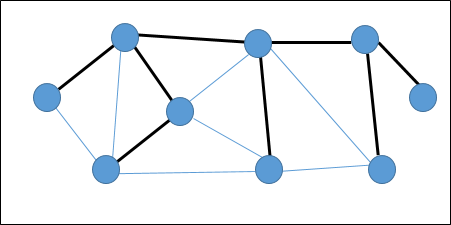
пример

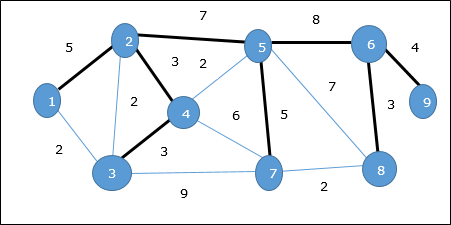
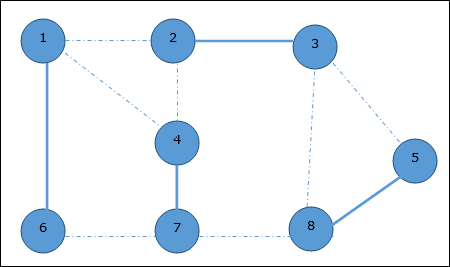
На следующем графике выделенные ребра образуют остовное дерево.

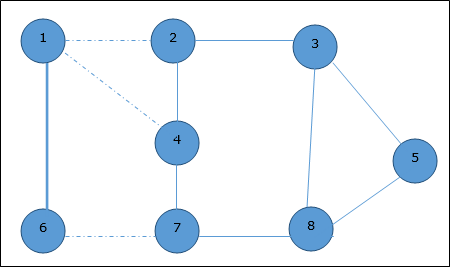
Минимальное остовное дерево

Минимальное связующее дерево (MST) — это подмножество ребер связного взвешенного неориентированного графа, который соединяет все вершины вместе с минимально возможным общим весом ребер. Чтобы получить MST, можно использовать алгоритм Прима или алгоритм Крускала. Следовательно, мы обсудим алгоритм Прима в этой главе.

Как мы уже обсуждали, один граф может иметь более одного связующего дерева. Если имеется n вершин, связующее дерево должно иметь n — 1 число ребер. В этом контексте, если каждое ребро графа связано с весом и существует более одного остовного дерева, нам нужно найти минимальное остовное дерево графа.

Кроме того, если существуют дублированные взвешенные ребра, граф может иметь несколько минимальных остовных деревьев.

На приведенном выше графике мы показали связующее дерево, хотя это не минимальное остовное дерево. Стоимость этого связующего дерева (5 + 7 + 3 + 3 + 5 + 8 + 3 + 4) = 38.

Мы будем использовать алгоритм Прима, чтобы найти минимальное остовное дерево.

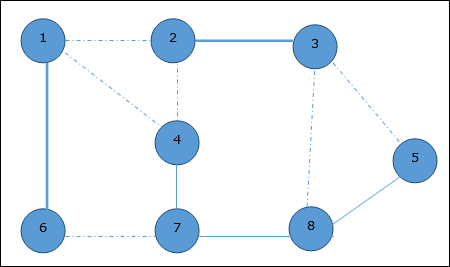
Алгоритм Прима

Алгоритм Прима — это жадный подход к поиску минимального остовного дерева. В этом алгоритме, чтобы сформировать MST, мы можем начать с произвольной вершины.

Algorithm: MST-Prim’s (G, w, r) 
for each u є G.V 
   u.key = ∞ 
   u.∏ = NIL 
r.key = 0 
Q = G.V 
while Q ≠ Ф 
   u = Extract-Min (Q) 
   for each v є G.adj[u] 
      if each v є Q and w(u, v) < v.key 
         v.∏ = u 
         v.key = w(u, v) 

Функция Extract-Min возвращает вершину с минимальной стоимостью ребра. Эта функция работает на минимальной куче.

пример

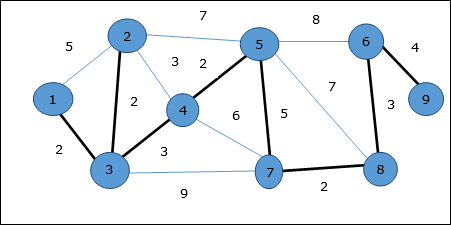
Используя алгоритм Прима, мы можем начать с любой вершины, начнем с вершины 1 .

Вершина 3 соединяется с вершиной 1 с минимальной стоимостью ребра, поэтому ребро (1, 2) добавляется в остовное дерево.

Далее рассматривается ребро (2, 3), так как это минимум среди ребер {(1, 2), (2, 3), (3, 4), (3, 7)} .

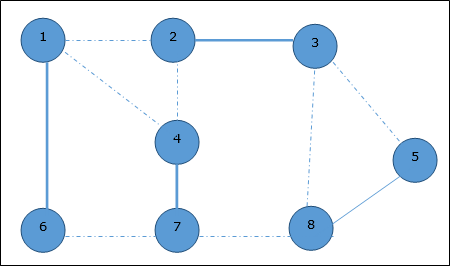
На следующем шаге мы получаем ребро (3, 4) и (2, 4) с минимальными затратами. Край (3, 4) выбирается случайным образом.

Аналогичным образом выбираются ребра (4, 5), (5, 7), (7, 8), (6, 8) и (6, 9) . Поскольку все вершины посещены, алгоритм останавливается.

Стоимость связующего дерева составляет (2 + 2 + 3 + 2 + 5 + 2 + 3 + 4) = 23. В этом графе больше нет связующего дерева со стоимостью менее 23 .

DAA — кратчайшие пути

Алгоритм Дейкстры

Алгоритм Дейкстры решает проблему кратчайших путей из одного источника на ориентированном взвешенном графе G = (V, E) , где все ребра неотрицательны (т. Е. W (u, v) ≥ 0 для каждого ребра (u, v). ) Є Д ).

В следующем алгоритме мы будем использовать одну функцию Extract-Min () , которая извлекает узел с наименьшим ключом.

Algorithm: Dijkstra’s-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
S := Ф 
Q := G.V 
while Q ≠ Ф 
   u := Extract-Min (Q) 
   S := S U {u} 
   for each vertex v Є G.adj[u] 
      if v.d > u.d + w(u, v) 
         v.d := u.d + w(u, v) 
         v.∏ := u

Анализ

Сложность этого алгоритма полностью зависит от реализации функции Extract-Min. Если функция извлечения min реализована с использованием линейного поиска, сложность этого алгоритма составляет O (V ² + E) .

В этом алгоритме, если мы используем min-heap, в которой работает функция Extract-Min (), чтобы вернуть узел из Q с наименьшим ключом, сложность этого алгоритма может быть дополнительно уменьшена.

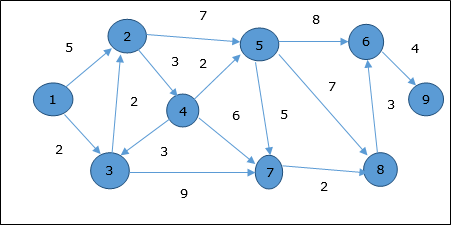
пример

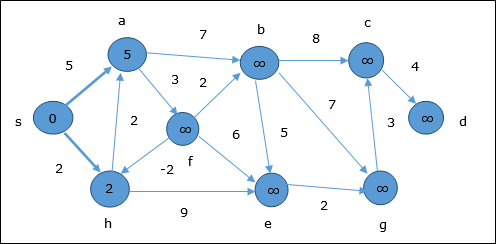
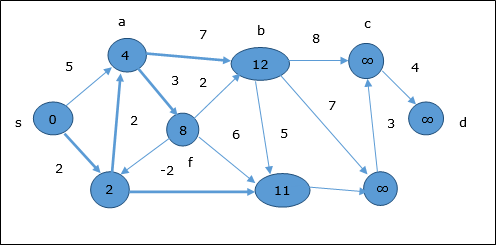
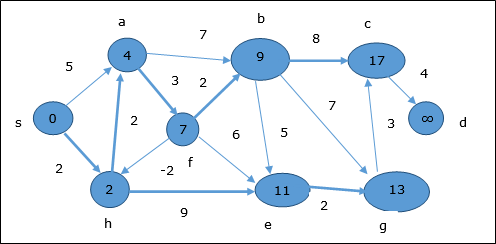
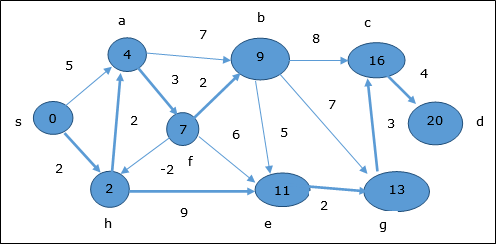
Рассмотрим вершину 1 и 9 как начальную и конечную вершины соответственно. Первоначально все вершины, кроме начальной, отмечены ∞, а начальная вершина — 0 .

темя	начальный	Step1 V 1	Step2 V 3	Step3 V 2	Step4 V 4	Step5 V 5	Step6 V 7	Step7 V 8	Step8 V 6
1	0	0	0	0	0	0	0	0	0
2	∞	5	4	4	4	4	4	4	4
3	∞	2	2	2	2	2	2	2	2
4	∞	∞	∞	7	7	7	7	7	7
5	∞	∞	∞	11	9	9	9	9	9
6	∞	∞	∞	∞	∞	17	17	16	16
7	∞	∞	11	11	11	11	11	11	11
8	∞	∞	∞	∞	∞	16	13	13	13
9	∞	∞	∞	∞	∞	∞	∞	∞	20

Следовательно, минимальное расстояние вершины 9 от вершины 1 составляет 20 . И путь

1 → 3 → 7 → 8 → 6 → 9

Этот путь определяется на основе информации предшественника.

Алгоритм Беллмана Форда

Этот алгоритм решает проблему кратчайшего пути с одним источником для ориентированного графа G = (V, E), в котором веса ребер могут быть отрицательными. Более того, этот алгоритм может быть применен для поиска кратчайшего пути, если не существует отрицательного взвешенного цикла.

Algorithm: Bellman-Ford-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
for i = 1 to |G.V| - 1 
   for each edge (u, v) Є G.E 
      if v.d > u.d + w(u, v) 
         v.d := u.d +w(u, v) 
         v.∏ := u 
for each edge (u, v) Є G.E 
   if v.d > u.d + w(u, v) 
      return FALSE 
return TRUE

Анализ

Первый цикл for используется для инициализации, которая выполняется за O (V) раз. Следующий цикл работает | V — 1 | проходит по краям, что занимает O (E) раз.

Следовательно, алгоритм Беллмана-Форда выполняется за время O (V, E) .

пример

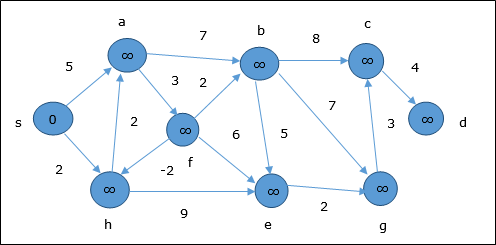
В следующем примере показано, как работает алгоритм Беллмана-Форда шаг за шагом. Этот граф имеет отрицательное ребро, но не имеет отрицательного цикла, поэтому проблему можно решить с помощью этой техники.

Во время инициализации все вершины, кроме источника, отмечены ∞, а источник — 0 .

На первом этапе все вершины, доступные из источника, обновляются с минимальными затратами. Следовательно, вершины a и h обновляются.

На следующем шаге вершины a, b, f и e обновляются.

Следуя той же логике, на этом шаге вершины b, f, c и g обновляются.

Здесь вершины c и d обновляются.

Следовательно, минимальное расстояние между вершиной s и вершиной d составляет 20 .

На основании информации предшественника путь s → h → e → g → c → d

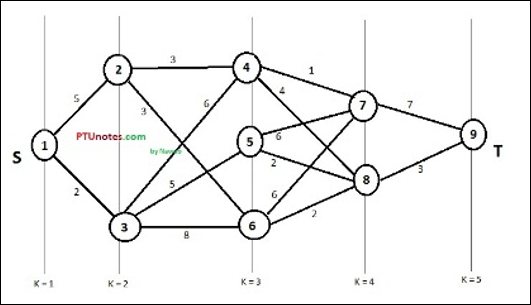
DAA — многоступенчатый график

Многоступенчатый граф G = (V, E) — это ориентированный граф, в котором вершины разбиты на k (где k > 1 ) число непересекающихся подмножеств S = {s ₁ , s ₂ ,…, s _k }, таких что ребро (u, v) находится в E, тогда u Є s _i и v Є s _{1 + 1} для некоторых подмножеств в разбиении и | с ₁ | = | с _к | = 1

Вершина s Є s ₁ называется источником, а вершина t Є s _k называется стоком .

G обычно считается взвешенным графом. На этом графике стоимость ребра (i, j) представлена c (i, j) . Следовательно, стоимость пути от источника s до приемника t является суммой затрат каждого ребра в этом пути.

Проблема многоступенчатого графа заключается в поиске пути с минимальными затратами от источника s до приемника t .

пример

Рассмотрим следующий пример, чтобы понять концепцию многоступенчатого графа.

Согласно формуле, мы должны рассчитать стоимость (i, j), используя следующие шаги

Шаг 1: Стоимость (K-2, j)

На этом этапе три узла (узел 4, 5. 6) выбираются как j . Следовательно, у нас есть три варианта выбора минимальной стоимости на этом этапе.

Стоимость (3, 4) = min {c (4, 7) + Стоимость (7, 9), c (4, 8) + Стоимость (8, 9)} = 7

Стоимость (3, 5) = min {c (5, 7) + Стоимость (7, 9), c (5, 8) + Стоимость (8, 9)} = 5

Стоимость (3, 6) = min {c (6, 7) + Стоимость (7, 9), c (6, 8) + Стоимость (8, 9)} = 5

Шаг 2: Стоимость (K-3, j)

Два узла выбраны как j, потому что на этапе k — 3 = 2 есть два узла, 2 и 3. Таким образом, значение i = 2 и j = 2 и 3.

Стоимость (2, 2) = min {c (2, 4) + Стоимость (4, 8) + Стоимость (8, 9), c (2, 6) +

Стоимость (6, 8) + Стоимость (8, 9)} = 8

Стоимость (2, 3) = {c (3, 4) + Стоимость (4, 8) + Стоимость (8, 9), c (3, 5) + Стоимость (5, 8) + Стоимость (8, 9), c (3, 6) + Стоимость (6, 8) + Стоимость (8, 9)} = 10

Шаг 3: Стоимость (K-4, j)

Стоимость (1, 1) = {c (1, 2) + Стоимость (2, 6) + Стоимость (6, 8) + Стоимость (8, 9), с (1, 3) + Стоимость (3, 5) + Стоимость (5, 8) + Стоимость (8, 9))} = 12

c (1, 3) + Стоимость (3, 6) + Стоимость (6, 8 + Стоимость (8, 9))} = 13

Следовательно, путь с минимальной стоимостью составляет 1 → 3 → 5 → 8 → 9 .

DAA — проблема коммивояжера

Постановка задачи

Путешественник должен посетить все города из списка, где известны расстояния между всеми городами, и каждый город должен быть посещен только один раз. По какому кратчайшему маршруту он посещает каждый город ровно один раз и возвращается в исходный город?

Решение

Проблема коммивояжера — самая известная вычислительная проблема. Мы можем использовать метод грубой силы, чтобы оценить каждый возможный тур и выбрать лучший. Для n числа вершин в графе существует ( n — 1)! количество возможностей.

Вместо грубой силы, использующей подход динамического программирования, решение может быть получено за меньшее время, хотя нет алгоритма полиномиального времени.

Рассмотрим граф G = (V, E) , где V — множество городов, а E — множество взвешенных ребер. Ребро e (u, v) обозначает, что вершины u и v связаны. Расстояние между вершиной u и v равно d (u, v) , что должно быть неотрицательным.

Предположим, мы начали с города 1 и, посетив некоторые города, теперь мы находимся в городе j . Следовательно, это частичный тур. Нам, безусловно, нужно знать j , так как это определит, какие города удобнее всего посетить в следующем. Нам также нужно знать все города, которые мы посетили, чтобы не повторять ни один из них. Следовательно, это соответствующая подзадача.

Для подмножества городов S Є {1, 2, 3, …, n}, которое включает 1 , и j Є S , пусть C (S, j) будет длина кратчайшего пути, посещающего каждый узел в S ровно один раз начиная с 1 и заканчивая j .

Когда | S | > 1, мы определяем C (S, 1) = ∝, поскольку путь не может начинаться и заканчиваться на 1 .

Теперь, давайте выразим C (S, j) в терминах меньших подзадач. Нам нужно начинать с 1 и заканчивать на j . Мы должны выбрать следующий город таким образом, чтобы

$$C (S, j) = min \: C (S - \ lbrace j \ rbrace, i) + d (i, j) \: где \: i \ in S \: и \: i \ neq jc ( S, j) = minC (s- \ lbrace j \ rbrace, i) + d (i, j) \: где \: i \ in S \: и \: i \ neq j$$

Algorithm: Traveling-Salesman-Problem 
C ({1}, 1) = 0 
for s = 2 to n do 
   for all subsets S Є {1, 2, 3, … , n} of size s and containing 1 
      C (S, 1) = ∞ 
   for all j Є S and j ≠ 1 
      C (S, j) = min {C (S – {j}, i) + d(i, j) for i Є S and i ≠ j} 
Return minj C ({1, 2, 3, …, n}, j) + d(j, i) 

Анализ

Существует не более $2 ^ nn$ подзадач, каждая из которых требует линейного времени для решения. Следовательно, общее время работы составляет $O (2 ^ nn ^ 2)$.

пример

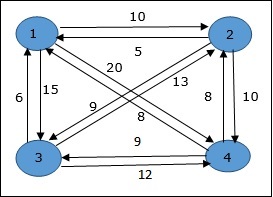
В следующем примере мы проиллюстрируем шаги для решения проблемы коммивояжера.

Из приведенного выше графика подготовлена ​​следующая таблица.

	1	2	3	4
1	0	10	15	20
2	5	0	9	10
3	6	13	0	12
4	8	8	9	0

S = Φ

$$\ small Cost (2, \ Phi, 1) = d (2,1) = 5 \ small Cost (2, \ Phi, 1) = d (2,1) = 5$$

$$\ small Cost (3, \ Phi, 1) = d (3,1) = 6 \ small Cost (3, \ Phi, 1) = d (3,1) = 6$$

$$\ small Cost (4, \ Phi, 1) = d (4,1) = 8 \ small Cost (4, \ Phi, 1) = d (4,1) = 8$$

S = 1

$$\ small Cost (i, s) = min \ lbrace Cost (j, s - (j)) + d [i, j] \ rbrace \ small Cost (i, s) = min \ lbrace Cost (j, s ) - (j)) + d [i, j] \ rbrace$$

$$\ small Cost (2, \ lbrace 3 \ rbrace, 1) = d [2,3] + Cost (3, \ Phi, 1) = 9 + 6 = 15 стоимости (2, \ lbrace3 \ rbrace, 1) = d [2,3] + стоимость (3, \ Phi, 1) = 9 + 6 = 15$$

$$\ small Cost (2, \ lbrace 4 \ rbrace, 1) = d [2,4] + Cost (4, \ Phi, 1) = 10 + 8 = 18 cost (2, \ lbrace4 \ rbrace, 1) = д [2,4] + стоимость (4, \ Фи, 1) = 10 + 8 = 18$$

$$\ small Cost (3, \ lbrace 2 \ rbrace, 1) = d [3,2] + Cost (2, \ Phi, 1) = 13 + 5 = 18 ccost (3, \ lbrace2 \ rbrace, 1) = d [3,2] + стоимость (2, \ Фи, 1) = 13 + 5 = 18$$

$$\ small Cost (3, \ lbrace 4 \ rbrace, 1) = d [3,4] + Cost (4, \ Phi, 1) = 12 + 8 = 20 стоимости (3, \ lbrace4 \ rbrace, 1) = д [3,4] + стоимость (4, \ Фи, 1) = 12 + 8 = 20$$

$$\ small Cost (4, \ lbrace 3 \ rbrace, 1) = d [4,3] + Cost (3, \ Phi, 1) = 9 + 6 = 15 стоимости (4, \ lbrace3 \ rbrace, 1) = д [4,3] + стоимость (3, \ Фи, 1) = 9 + 6 = 15$$

$$\ small Cost (4, \ lbrace 2 \ rbrace, 1) = d [4,2] + Cost (2, \ Phi, 1) = 8 + 5 = 13cost (4, \ lbrace2 \ rbrace, 1) = д [4,2] + стоимость (2, \ Фи, 1) = 8 + 5 = 13$$

S = 2

$$\ small Cost (2, \ lbrace 3, 4 \ rbrace, 1) = \ begin {case} d [2, 3] + Стоимость (3, \ lbrace 4 \ rbrace, 1) = 9 + 20 = 29 \ \ d [2, 4] + Стоимость (4, \ lbrace 3 \ rbrace, 1) = 10 + 15 = 25 = 25 \ small Стоимость (2, \ lbrace 3,4 \ rbrace, 1) \\\ lbrace d [ 2,3] + \ small cost (3, \ lbrace4 \ rbrace, 1) = 9 + 20 = 29d [2,4] + \ small Cost (4, \ lbrace 3 \ rbrace, 1) = 10 + 15 = 25 \ end {case} = 25$$

$$\ small Cost (3, \ lbrace 2, 4 \ rbrace, 1) = \ begin {case} d [3, 2] + Cost (2, \ lbrace 4 \ rbrace, 1) = 13 + 18 = 31 \ \ d [3, 4] + Стоимость (4, \ lbrace 2 \ rbrace, 1) = 12 + 13 = 25 = 25 \ small Стоимость (3, \ lbrace 2,4 \ rbrace, 1) \\\ lbrace d [ 3,2] + \ small cost (2, \ lbrace4 \ rbrace, 1) = 13 + 18 = 31d [3,4] + \ small Cost (4, \ lbrace 2 \ rbrace, 1) = 12 + 13 = 25 \ end {case} = 25$$

$$\ small Cost (4, \ lbrace 2, 3 \ rbrace, 1) = \ begin {case} d [4, 2] + Cost (2, \ lbrace 3 \ rbrace, 1) = 8 + 15 = 23 \ \ d [4, 3] + Cost (3, \ lbrace 2 \ rbrace, 1) = 9 + 18 = 27 = 23 \ small Стоимость (4, \ lbrace 2,3 \ rbrace, 1) \\\ lbrace d [ 4,2] + \ small cost (2, \ lbrace3 \ rbrace, 1) = 8 + 15 = 23d [4,3] + \ small Cost (3, \ lbrace 2 \ rbrace, 1) = 9 + 18 = 27 \ end {case} = 23$$

S = 3

$$\ small Cost (1, \ lbrace 2, 3, 4 \ rbrace, 1) = \ begin {case} d [1, 2] + Стоимость (2, \ lbrace 3, 4 \ rbrace, 1) = 10 + 25 = 35 \ d [1, 3] + Стоимость (3, \ lbrace 2, 4 \ rbrace, 1) = 15 + 25 = 40 \\ d [1, 4] + Стоимость (4, \ lbrace 2, 3 1) = 20 + 23 = 43 = 35 затрат (1, 2,3,4,4), 1) \ 1,2 [+] стоимости (2 3,4,4) , 1) = 10 + 25 = 35 \ d [1,3] + стоимость (3, 2,4 фунта, 1) = 15 + 25 = 40 \ 1,4 [+] + стоимость (4 , \ lbrace 2,3 \ rbrace, 1) = 20 + 23 = 43 = 35 \ end {case}$$

Минимальная стоимость пути составляет 35.

Начнем со стоимости {1, {2, 3, 4}, 1} , получим минимальное значение для d [1, 2] . Когда s = 3 , выберите путь от 1 до 2 (стоимость 10), затем вернитесь назад. Когда s = 2 , мы получаем минимальное значение для d [4, 2] . Выберите путь от 2 до 4 (стоимость 10), затем идите назад.

Когда s = 1 , мы получаем минимальное значение для d [4, 3] . Выбрав путь от 4 до 3 (стоимость 9), мы перейдем к шагу s = Φ . Получаем минимальное значение для d [3, 1] (стоимость 6).

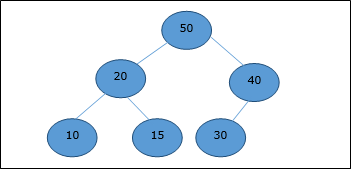
DAA — Деревья бинарного поиска с оптимальной стоимостью

Двоичное дерево поиска (BST) — это дерево, в котором значения ключей хранятся во внутренних узлах. Внешние узлы являются нулевыми узлами. Ключи упорядочены лексикографически, то есть для каждого внутреннего узла все ключи в левом поддереве меньше, чем ключи в узле, а все ключи в правом поддереве больше.

Когда мы знаем частоту поиска каждого из ключей, довольно легко вычислить ожидаемую стоимость доступа к каждому узлу в дереве. Оптимальным бинарным деревом поиска является BST, у которого минимальная ожидаемая стоимость определения местоположения каждого узла.

Время поиска элемента в BST равно O (n) , тогда как в сбалансированном BST время поиска равно O (log n) . Опять же, время поиска можно улучшить в дереве бинарного поиска с оптимальной стоимостью, размещая наиболее часто используемые данные в корне и ближе к корневому элементу, а наименее часто используемые данные — рядом с листьями и листьями.

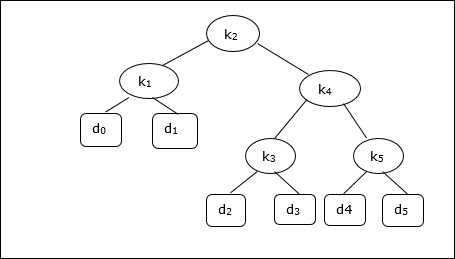
Здесь представлен алгоритм оптимального бинарного дерева поиска. Сначала мы строим BST из набора предоставленных n различных ключей <k ₁ , k ₂ , k ₃ , … k _n > . Здесь мы предполагаем, что вероятность доступа к ключу K _i равна p _i . Добавлены некоторые фиктивные ключи ( d ₀ , d ₁ , d ₂ , … d _n ), поскольку могут быть выполнены некоторые поиски для значений, которых нет в наборе ключей K. Мы предполагаем, что для каждого фиктивного ключа d _i вероятность доступа равна q _i .

Optimal-Binary-Search-Tree(p, q, n) 
e[1…n + 1, 0…n],  
w[1…n + 1, 0…n], 
root[1…n + 1, 0…n]  
for i = 1 to n + 1 do 
   e[i, i - 1] := q i - 1 
   w[i, i - 1] := q i - 1  
for l = 1 to n do 
   for i = 1 to n – l + 1 do 
      j = i + l – 1 e[i, j] := ∞ 
      w[i, i] := w[i, i -1] + p j + q j 
      for r = i to j do 
         t := e[i, r - 1] + e[r + 1, j] + w[i, j] 
         if t < e[i, j] 
            e[i, j] := t 
            root[i, j] := r 
return e and root 

Анализ

Алгоритм требует времени O (n ³ ) , поскольку используются три вложенных цикла for . Каждый из этих циклов принимает не более n значений.

пример

Учитывая следующее дерево, стоимость составляет 2,80, хотя это не оптимальный результат.

Узел	глубина	Вероятность	Вклад
к 1	1	0,15	0,30
к 2	0	0,10	0,10
к 3	2	0,05	0,15
к 4	1	0,10	0,20
к 5	2	0,20	0,60
д 0	2	0,05	0,15
д 1	2	0,10	0,30
д 2	3	0,05	0,20
д 3	3	0,05	0,20
д 4	3	0,05	0,20
д 5	3	0,10	0,40
Всего			2,80

Чтобы получить оптимальное решение, используя алгоритм, обсуждаемый в этой главе, создаются следующие таблицы.

В следующих таблицах индекс столбца равен i, а индекс строки равен j .

е	1	2	3	4	5	6
5	2,75	2,00	1,30	0,90	0,50	0,10
4	1,75	1,20	0,60	0,30	0,05
3	1,25	0,70	0,25	0,05
2	0,90	0,40	0,05
1	0,45	0,10
0	0,05

вес	1	2	3	4	5	6
5	1,00	0,80	0,60	0,50	0,35	0,10
4	0,70	0,50	0,30	0,20	0,05
3	0,55	0,35	0,15	0,05
2	0,45	0,25	0,05
1	0,30	0,10
0	0,05

корень	1	2	3	4	5
5	2	4	5	5	5
4	2	2	4	4
3	2	2	3
2	1	2
1	1

Из этих таблиц можно сформировать оптимальное дерево.

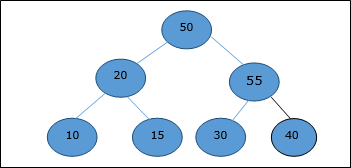
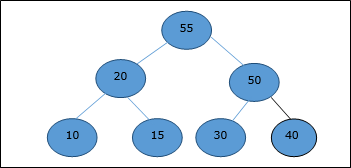
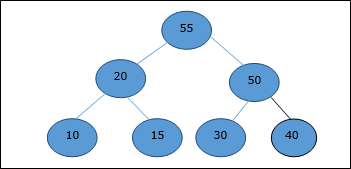
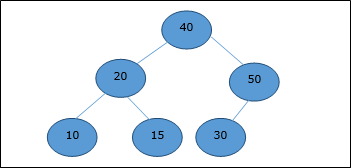
DAA — двоичная куча

Существует несколько типов куч, однако в этой главе мы собираемся обсудить двоичную кучу. Бинарная куча — это структура данных, которая выглядит как полное двоичное дерево. Структура данных кучи подчиняется свойствам упорядочения, описанным ниже. Обычно куча представлена ​​массивом. В этой главе мы представляем кучу H.

Поскольку элементы кучи хранятся в массиве, учитывая начальный индекс как 1 , положение родительского узла i- ^го элемента можно найти в ⌊ i / 2 ⌋ . Левый и правый дочерние элементы i- ^го узла находятся в положении 2i и 2i + 1 .

Двоичная куча может быть классифицирована далее как максимальная куча или минимальная куча на основе свойства упорядочения.

Max-Heap

В этой куче значение ключа узла больше или равно значению ключа самого высокого дочернего элемента.

Следовательно, H [Parent (i)] ≥ H [i]

Min-Heap

В средней куче значение ключа узла меньше или равно значению ключа самого нижнего потомка.

Следовательно, H [Parent (i)] ≤ H [i]

В этом контексте основные операции показаны ниже относительно Max-Heap. Для вставки и удаления элементов в кучах и из них требуется перестановка элементов. Следовательно, функция Heapify должна быть вызвана.

Представление массива

Полное двоичное дерево может быть представлено массивом, хранящим его элементы с использованием обхода порядка уровней.

Давайте рассмотрим кучу (как показано ниже), которая будет представлена ​​массивом H.

Рассматривая начальный индекс как 0 , используя обход уровня, элементы сохраняются в массиве следующим образом.

Индекс	0	1	2	3	4	5	6	7	8	…
элементы	70	30	50	12	20	35	25	4	8	…

В этом контексте операции с кучей представляются в отношении Max-Heap.

Чтобы найти индекс родителя элемента по индексу i , используется следующий алгоритм Parent (numbers [], i) .

Algorithm: Parent (numbers[], i) 
if i == 1 
   return NULL 
else 
   [i / 2]

Индекс левого потомка элемента с индексом i можно найти с помощью следующего алгоритма Left-Child (numbers [], i) .

Algorithm: Left-Child (numbers[], i) 
If 2 * i ≤ heapsize 
   return [2 * i] 
else 
   return NULL 

Индекс правого потомка элемента по индексу i можно найти с помощью следующего алгоритма Right-Child (numbers [], i) .

Algorithm: Right-Child (numbers[], i) 
if 2 * i < heapsize 
   return [2 * i + 1] 
else 
   return NULL

DAA — метод вставки

Чтобы вставить элемент в кучу, новый элемент изначально добавляется в конец кучи как последний элемент массива.

После вставки этого элемента свойство heap может быть нарушено, следовательно, свойство heap восстанавливается путем сравнения добавленного элемента с его родительским элементом и перемещения добавленного элемента на уровень, меняя позиции с родительским. Этот процесс называется перколяцией .

Сравнение повторяется до тех пор, пока родительский элемент не станет больше или равен перколирующему элементу.

Algorithm: Max-Heap-Insert (numbers[], key) 
heapsize = heapsize + 1 
numbers[heapsize] = -∞ 
i = heapsize 
numbers[i] = key 
while i > 1 and numbers[Parent(numbers[], i)] < numbers[i] 
   exchange(numbers[i], numbers[Parent(numbers[], i)]) 
   i = Parent (numbers[], i) 

Анализ

Первоначально, элемент добавляется в конец массива. Если он нарушает свойство heap, элемент обменивается с его родителем. Высота дерева равна log n . Максимальный журнал n количество операций, которые необходимо выполнить.

Следовательно, сложность этой функции составляет O (log n) .

пример

Давайте рассмотрим максимальную кучу, как показано ниже, где необходимо добавить новый элемент 5.

Первоначально 55 будет добавлено в конце этого массива.

После вставки он нарушает свойство кучи. Следовательно, элемент должен поменяться с его родителем. После подкачки куча выглядит следующим образом.

Опять же, элемент нарушает свойство кучи. Следовательно, он поменяется с родителем.

Теперь мы должны остановиться.

DAA — метод Heapify

Метод heapify переставляет элементы массива, где левое и правое поддерево i- ^го элемента подчиняется свойству heap.

Algorithm: Max-Heapify(numbers[], i) 
leftchild := numbers[2i] 
rightchild := numbers [2i + 1] 
if leftchild ≤ numbers[].size and numbers[leftchild] > numbers[i] 
   largest := leftchild 
else 
   largest := i 
if rightchild ≤ numbers[].size and numbers[rightchild] > numbers[largest] 
   largest := rightchild 
if largest ≠ i 
   swap numbers[i] with numbers[largest] 
   Max-Heapify(numbers, largest)

Когда предоставленный массив не подчиняется свойству heap, Heap создается на основе следующего алгоритма Build-Max-Heap (numbers []) .

Algorithm: Build-Max-Heap(numbers[]) 
numbers[].size := numbers[].length 
fori = ⌊ numbers[].length/2 ⌋ to 1 by -1 
   Max-Heapify (numbers[], i) 

DAA — метод извлечения

Метод извлечения используется для извлечения корневого элемента кучи. Ниже приводится алгоритм.

Algorithm: Heap-Extract-Max (numbers[]) 
max = numbers[1] 
numbers[1] = numbers[heapsize] 
heapsize = heapsize – 1 
Max-Heapify (numbers[], 1) 
return max 

пример

Давайте рассмотрим тот же пример, который обсуждался ранее. Теперь мы хотим извлечь элемент. Этот метод вернет корневой элемент кучи.

После удаления корневого элемента последний элемент будет перемещен в корневую позицию.

Теперь будет вызвана функция Heapify. После Heapify создается следующая куча.

DAA — пузырьковая сортировка

Bubble Sort — это элементарный алгоритм сортировки, который работает путем многократного обмена смежными элементами, если это необходимо. Когда обмены не требуются, файл сортируется.

Это самый простой метод среди всех алгоритмов сортировки.

Algorithm: Sequential-Bubble-Sort (A) 
fori← 1 to length [A] do 
for j ← length [A] down-to i +1 do 
   if A[A] < A[j - 1] then 
      Exchange A[j] ↔ A[j-1] 

Реализация

voidbubbleSort(int numbers[], intarray_size) { 
   inti, j, temp; 
   for (i = (array_size - 1); i >= 0; i--) 
   for (j = 1; j <= i; j++) 
      if (numbers[j - 1] > numbers[j]) { 
         temp = numbers[j-1]; 
         numbers[j - 1] = numbers[j]; 
         numbers[j] = temp; 
      } 
} 

Анализ

Здесь количество сравнений

1 + 2 + 3 + … + ( n — 1) = n ( n — 1) / 2 = O ( n ² )

Ясно, что график показывает характер n ² типа пузырьков.

В этом алгоритме число сравнений не зависит от набора данных, т. Е. Находятся ли предоставленные входные элементы в отсортированном порядке или в обратном порядке или в случайном порядке.

Требование к памяти

Из алгоритма, изложенного выше, ясно, что сортировка пузырьков не требует дополнительной памяти.

пример

Несортированный список:

5 2 1 4 3 7 6

Несортированный список:

1- ^я итерация:

5> 2 своп	2 5 1 4 3 7 6
5> 1 своп	2 1 5 4 3 7 6
5> 4 своп	2 1 4 5 3 7 6
5> 3 своп	2 1 4 3 5 7 6
5 <7 без обмена	2 1 4 3 5 7 6
Своп 7> 6	2 1 4 3 5 6 7

5> 2 своп

5> 1 своп

5> 4 своп

5> 3 своп

5 <7 без обмена

Своп 7> 6

2- ^я итерация:

2> 1 своп	1 2 4 3 5 6 7
2 <4 без обмена	1 2 4 3 5 6 7
Своп 4> 3	1 2 3 4 5 6 7
4 <5 без обмена	1 2 3 4 5 6 7
5 <6 без обмена	1 2 3 4 5 6 7

2> 1 своп

2 <4 без обмена

Своп 4> 3

4 <5 без обмена

5 <6 без обмена

Нет изменений в 3- ^й , 4- ^й , 5- ^й и 6- ^й итерации.

В заключение,

отсортированный список

1 2 3 4 5 6 7

отсортированный список

DAA — вставка сортировки

Вставка сортировки — очень простой метод сортировки чисел в порядке возрастания или убывания. Этот метод следует инкрементному методу. Это можно сравнить с техникой сортировки карт во время игры.

Числа, которые необходимо отсортировать, называются ключами . Вот алгоритм метода сортировки вставок.

Algorithm: Insertion-Sort(A) 
for j = 2 to A.length 
   key = A[j] 
   i = j – 1 
   while i > 0 and A[i] > key 
      A[i + 1] = A[i] 
      i = i -1 
   A[i + 1] = key 

Анализ

Время выполнения этого алгоритма очень сильно зависит от заданного ввода.

Если данные числа отсортированы, этот алгоритм выполняется за O (n) раз. Если заданные числа в обратном порядке, алгоритм запускается за O (n ² ) времени.

пример

Несортированный список:

2 13 5 18 14

Несортированный список:

1- ^я итерация:

Ключ = [2] = 13

a [1] = 2 <13

Своп, без свопа

2 13 5 18 14

Своп, без свопа

2- ^я итерация:

Ключ = [3] = 5

a [2] = 13> 5

Поменяйте местами 5 и 13

2 5 13 18 14

Поменяйте местами 5 и 13

Далее a [1] = 2 <13

Своп, без свопа

2 5 13 18 14

Своп, без свопа

3- ^я итерация:

Ключ = [4] = 18

а [3] = 13 <18,

а [2] = 5 <18,

а [1] = 2 <18

Своп, без свопа

2 5 13 18 14

Своп, без свопа

4- ^я итерация:

Ключ = [5] = 14

а [4] = 18> 14

Поменять местами 18 и 14

2 5 13 14 18

Поменять местами 18 и 14

Далее а [3] = 13 <14,

а [2] = 5 <14,

а [1] = 2 <14

Так что без обмена

2 5 13 14 18

Так что без обмена

В заключение,

отсортированный список

2 5 13 14 18

отсортированный список

DAA — выбор сортировки

Этот тип сортировки называется « Выбор сортировки», так как он работает путем многократной сортировки элементов. Он работает следующим образом: сначала найдите наименьшее в массиве и обменяйте его с элементом в первой позиции, затем найдите второй наименьший элемент и обменяйте его на элемент во второй позиции, и продолжайте таким образом, пока весь массив не будет отсортирован.

Algorithm: Selection-Sort (A) 
fori ← 1 to n-1 do 
   min j ← i; 
   min x ← A[i] 
   for j ←i + 1 to n do 
      if A[j] < min x then 
         min j ← j 
         min x ← A[j] 
   A[min j] ← A [i] 
   A[i] ← min x 

Сортировка выбора является одним из самых простых методов сортировки, и она очень хорошо работает для небольших файлов. Он имеет довольно важное применение, поскольку каждый элемент перемещается не более одного раза.

Раздел сортировки — это метод выбора файлов с очень большими объектами (записями) и маленькими ключами. Наихудший случай возникает, если массив уже отсортирован в порядке убывания, и мы хотим отсортировать их в порядке возрастания.

Тем не менее, время, требуемое алгоритмом сортировки выбора, не очень чувствительно к исходному порядку сортируемого массива: проверка, если A [j] < min x , выполняется точно одинаковое количество раз в каждом случае.

Сортировка выбора тратит большую часть своего времени, пытаясь найти минимальный элемент в несортированной части массива. Это ясно показывает сходство между сортировкой Selection и Bubble.

• Пузырьковая сортировка выбирает максимальное количество оставшихся элементов на каждом этапе, но затрачивает некоторые усилия на наложение некоторого порядка на несортированную часть массива.

• Сортировка выбора является квадратичной как в худшем, так и в среднем случае, и не требует дополнительной памяти.

Пузырьковая сортировка выбирает максимальное количество оставшихся элементов на каждом этапе, но затрачивает некоторые усилия на наложение некоторого порядка на несортированную часть массива.

Сортировка выбора является квадратичной как в худшем, так и в среднем случае, и не требует дополнительной памяти.

Для каждого i от 1 до n — 1 существует один обмен и n — i сравнений, таким образом, имеется в общей сложности n — 1 обменов и

(n — 1) + (n — 2) + … + 2 + 1 = n (n — 1) / 2 сравнения.

Эти наблюдения верны, независимо от того, что входные данные.

В худшем случае это может быть квадратично, но в среднем это количество равно O (n log n) . Это означает, что время выполнения сортировки Selection довольно нечувствительно к вводу .

Реализация

Void Selection-Sort(int numbers[], int array_size) { 
   int i, j; 
   int min, temp;  
   for (i = 0; I < array_size-1; i++) { 
      min = i; 
      for (j = i+1; j < array_size; j++) 
         if (numbers[j] < numbers[min]) 
            min = j; 
      temp = numbers[i]; 
      numbers[i] = numbers[min]; 
      numbers[min] = temp; 
   } 
} 

пример

Несортированный список:

5 2 1 4 3

Несортированный список:

1- ^я итерация:

Наименьший = 5

2 <5, самый маленький = 2

1 <2, самый маленький = 1

4> 1, наименьшее = 1

3> 1, наименьшее = 1

Поменяйте местами 5 и 1

1 2 5 4 3

Поменяйте местами 5 и 1

2- ^я итерация:

Наименьший = 2

2 <5, самый маленький = 2

2 <4, самый маленький = 2

2 <3, самый маленький = 2

Нет своп

1 2 5 4 3

Нет своп

3- ^я итерация:

Наименьший = 5

4 <5, самый маленький = 4

3 <4, самый маленький = 3

Поменяйте местами 5 и 3

1 2 3 4 5

Поменяйте местами 5 и 3

4- ^я итерация:

Наименьший = 4

4 <5, самый маленький = 4

Нет своп

1 2 3 4 5

Нет своп

В заключение,

отсортированный список

1 2 3 4 5

отсортированный список

DAA — Быстрая сортировка

Используется по принципу «разделяй и властвуй». Быстрая сортировка — это алгоритм выбора во многих ситуациях, поскольку его нетрудно реализовать. Это хороший вид общего назначения, и он потребляет относительно меньше ресурсов во время выполнения.

преимущества

• Он на месте, поскольку использует только небольшой вспомогательный стек.

• Для сортировки n элементов требуется только n (log n) времени.

• У него очень короткая внутренняя петля.

• Этот алгоритм был подвергнут тщательному математическому анализу, можно сделать очень точное заявление о проблемах производительности.

Он на месте, поскольку использует только небольшой вспомогательный стек.

Для сортировки n элементов требуется только n (log n) времени.

У него очень короткая внутренняя петля.

Этот алгоритм был подвергнут тщательному математическому анализу, можно сделать очень точное заявление о проблемах производительности.

Недостатки

• Это рекурсивно. Особенно, если рекурсия недоступна, реализация чрезвычайно сложна.

• Это требует квадратичного (т.е. n2) времени в худшем случае.

• Он хрупок, то есть простая ошибка в реализации может остаться незамеченной и привести к ее плохой работе.

Это рекурсивно. Особенно, если рекурсия недоступна, реализация чрезвычайно сложна.

Это требует квадратичного (т.е. n2) времени в худшем случае.

Он хрупок, то есть простая ошибка в реализации может остаться незамеченной и привести к ее плохой работе.

Быстрая сортировка работает путем разбиения заданного массива A [p … r] на два непустых подмассива A [p … q] и A [q + 1 … r] так , чтобы каждый ключ в A [p … q] меньше или равно каждому ключу в A [q + 1 … r] .

Затем два подмассива сортируются рекурсивными вызовами быстрой сортировки. Точная позиция раздела зависит от заданного массива, и индекс q вычисляется как часть процедуры разделения.

Algorithm: Quick-Sort (A, p, r) 
if p < r then 
   q Partition (A, p, r) 
   Quick-Sort (A, p, q) 
   Quick-Sort (A, q + r, r) 

Обратите внимание, что для сортировки всего массива начальный вызов должен быть быстрой сортировки (A, 1, длина [A])

В качестве первого шага, быстрая сортировка выбирает один из элементов в массиве для сортировки в качестве сводной. Затем массив разделяется по обе стороны от оси. Элементы, которые меньше или равны повороту, будут двигаться влево, а элементы, которые больше или равны повороту, будут двигаться вправо.

Разбиение массива

Процедура разбиения переставляет суб-массивы на месте.

Function: Partition (A, p, r) 
x ← A[p] 
i ← p-1 
j ← r+1 
while TRUE do 
   Repeat j ← j - 1 
   until A[j] ≤ x  
   Repeat i← i+1 
   until A[i] ≥ x  
   if i < j then  
      exchange A[i] ↔ A[j] 
   else  
      return j 

Анализ

Наихудшая сложность алгоритма быстрой сортировки — O (n ² ) . Однако, используя эту технику, в средних случаях обычно мы получаем вывод за O (n log n) времени.

DAA — Radix Sort

Radix sort — это небольшой метод, который многие люди интуитивно используют при алфавитном расположении большого списка имен. В частности, список имен сначала сортируется по первой букве каждого имени, то есть имена расположены в 26 классах.

Интуитивно понятно, что можно отсортировать числа по их наиболее значимым цифрам. Однако сортировка Radix работает нелогично, сначала сортируя младшие разряды. При первом проходе все числа сортируются по младшей цифре и объединяются в массив. Затем на втором проходе все числа снова сортируются по вторым младшим разрядам и объединяются в массив и так далее.

Algorithm: Radix-Sort (list, n) 
shift = 1 
for loop = 1 to keysize do 
   for entry = 1 to n do 
      bucketnumber = (list[entry].key / shift) mod 10 
      append (bucket[bucketnumber], list[entry]) 
   list = combinebuckets() 
   shift = shift * 10 

Анализ

Каждая клавиша просматривается сразу для каждой цифры (или буквы, если клавиши алфавитные) самой длинной клавиши. Следовательно, если самый длинный ключ имеет m цифр и n ключей, радикальная сортировка имеет порядок O (mn) .

Однако, если мы посмотрим на эти два значения, размер ключей будет относительно небольшим по сравнению с количеством ключей. Например, если у нас есть шестизначные ключи, у нас может быть миллион разных записей.

Здесь мы видим, что размер ключей несущественен, и этот алгоритм имеет линейную сложность O (n) .

пример

Следующий пример показывает, как сортировка Radix работает с семью 3-значными числами.

вход	1- й проход	2- й проход	3- й проход
329	720	720	329
457	355	329	355
657	436	436	436
+839	457	+839	457
436	657	355	657
720	329	457	720
355	+839	657	+839

В приведенном выше примере первый столбец является входным. Остальные столбцы показывают список после последовательных сортировок в позиции все более значимых цифр. Код для сортировки Radix предполагает, что каждый элемент в массиве A из n элементов имеет d цифр, где цифра 1 — цифра самого младшего разряда, а d — цифра высшего порядка.

Детерминированные и недетерминированные вычисления

Чтобы понять класс P и NP , сначала мы должны знать вычислительную модель. Следовательно, в этой главе мы обсудим две важные вычислительные модели.

Детерминированные вычисления и класс P

Детерминированная машина Тьюринга

Одной из таких моделей является детерминированная однотонная машина Тьюринга. Эта машина состоит из управления конечным состоянием, головки чтения-записи и двусторонней ленты с бесконечной последовательностью.

Ниже приведена принципиальная схема детерминированной одноленточной машины Тьюринга.

Программа для детерминированной машины Тьюринга определяет следующую информацию:

• Конечный набор символов ленты (символы ввода и пустой символ)
• Конечный набор состояний
• Функция перехода

В алгоритмическом анализе, если задача решается за полиномиальное время детерминированной ленточной машиной Тьюринга, проблема принадлежит классу P.

Недетерминированные вычисления и класс NP

Недетерминированная машина Тьюринга

Чтобы решить вычислительную задачу, другой моделью является недетерминированная машина Тьюринга (NDTM). Структура NDTM похожа на DTM, однако здесь у нас есть еще один дополнительный модуль, известный как модуль угадывания, который связан с одной головой только для записи.

Ниже приведена принципиальная схема.

Если задача решается за полиномиальное время с помощью недетерминированной машины Тьюринга, задача принадлежит классу NP.

DAA — Макс Клик

В неориентированном графе клика является полным подграфом данного графа. Полный подграф означает, что все вершины этого подграфа связаны со всеми остальными вершинами этого подграфа.

Задача Макса-Клика является вычислительной задачей нахождения максимальной клики графа. Макс клика используется во многих реальных задачах.

Давайте рассмотрим приложение для социальных сетей, где вершины представляют профиль людей, а ребра — взаимное знакомство в графе. На этом графике клика представляет собой подмножество людей, которые все знают друг друга.

Чтобы найти максимальную клику, можно систематически проверять все подмножества, но этот вид поиска методом «грубой силы» слишком трудоемкий для сетей, содержащих более нескольких десятков вершин.

 Алгоритм: Макс-Клик (G, n, k) 
 S: = Φ 
 для I = 1 до K сделать 
    t: = выбор (1… n)  
    если t Є S, то 
       возврат неудачи 
    S: = S ∪ t  
 для всех пар (i, j) таких, что i Є S и j Є S и i ≠ j делают 
    если (i, j) не является ребром графа, то  
       возврат неудачи 
 вернуть успех 

Анализ

Задача Макса-Клика является недетерминированным алгоритмом. В этом алгоритме сначала мы пытаемся определить набор из k различных вершин, а затем мы пытаемся проверить, образуют ли эти вершины полный граф.

Для решения этой проблемы не существует детерминированного алгоритма за полиномиальное время. Эта проблема NP-Complete.

пример

Посмотрите на следующий график. Здесь подграф, содержащий вершины 2, 3, 4 и 6, образует полный граф. Следовательно, этот подграф является кликой . Так как это максимально полный подграф представленного графа, это 4-клика .

DAA — Vertex Cover

Покрытие вершины неориентированного графа G = (V, E) является подмножеством вершин V ^‘ ⊆ V таким, что если ребро (u, v) является ребром G , то либо u в V, либо v в V ^‘, либо и то и другое.

Найти покрытие вершины максимального размера в данном неориентированном графе. Это оптимальное вершинное раскрытие является оптимизационной версией NP-полной задачи. Однако не так сложно найти покрытие вершин, близкое к оптимальному.

APPROX-VERTEX_COVER (G: Graph) c ← { } E ' ← E[G] 
while E ' is not empty do 
   Let (u, v) be an arbitrary edge of E ' c ← c U {u, v} 
   Remove from E ' every edge incident on either u or v 
return c

пример

Множество ребер данного графа —

{(1,6), (1,2), (1,4), (2,3), (2,4), (6,7), (4,7), (7,8), ( 3,8), (3,5), (8,5)}

Теперь мы начнем с выбора произвольного ребра (1,6). Мы удаляем все ребра, которые либо падают на вершину 1 или 6, и добавляем ребро (1,6) для покрытия.

На следующем шаге мы выбрали другое ребро (2,3) наугад

Теперь мы выбираем другое ребро (4,7).

Выбираем другое ребро (8,5).

Следовательно, вершинное покрытие этого графа равно {1,2,4,5}.

Анализ

Легко видеть, что время выполнения этого алгоритма составляет O (V + E) , используя список смежности для представления E ^‘ .

DAA — класс P & NP

В области компьютерных наук многие проблемы решаются, когда цель состоит в том, чтобы максимизировать или минимизировать некоторые значения, тогда как в других задачах мы пытаемся выяснить, есть ли решение или нет. Следовательно, проблемы могут быть классифицированы следующим образом —

Задача оптимизации

Проблемы оптимизации — те, для которых цель состоит в том, чтобы максимизировать или минимизировать некоторые значения. Например,

• Нахождение минимального количества цветов, необходимых для раскраски данного графика.

• Нахождение кратчайшего пути между двумя вершинами графа.

Нахождение минимального количества цветов, необходимых для раскраски данного графика.

Нахождение кратчайшего пути между двумя вершинами графа.

Решение проблемы

Существует много проблем, для которых ответом является «да» или «нет». Эти типы проблем известны как проблемы с решением . Например,

• Может ли данный график быть окрашен только в 4 цвета.

• Нахождение гамильтонова цикла в графе не является проблемой решения, тогда как проверка графа является гамильтоновой или нет — это проблема решения.

Может ли данный график быть окрашен только в 4 цвета.

Нахождение гамильтонова цикла в графе не является проблемой решения, тогда как проверка графа является гамильтоновой или нет — это проблема решения.

Что такое язык?

Каждое решение проблемы может иметь только два ответа, да или нет. Следовательно, решение проблемы может принадлежать языку, если он дает ответ «да» для конкретного ввода. Язык — это совокупность входных данных, ответ на которые положительный. Большинство алгоритмов, рассмотренных в предыдущих главах, являются алгоритмами полиномиального времени .

Для входного размера n , если временная сложность алгоритма для наихудшего случая равна O (n ^k ) , где k — константа, алгоритм — алгоритм полиномиального времени.

Такие алгоритмы, как умножение цепочки матриц, кратчайший путь из одного источника, кратчайший путь для всех пар, минимальное остовное дерево и т. Д., Выполняются за полиномиальное время. Однако существует много проблем, таких как путешествующий продавец, оптимальная раскраска графа, гамильтоновы циклы, поиск самого длинного пути в графе и удовлетворение булевой формулы, для которой не известны алгоритмы полиномиального времени. Эти проблемы относятся к интересному классу задач, называемых задачами NP-Complete , статус которых неизвестен.

В этом контексте мы можем классифицировать проблемы следующим образом:

Р-Класс

Класс P состоит из тех задач, которые разрешимы за полиномиальное время, то есть эти проблемы могут быть решены за время O (n ^k ) в худшем случае, где k является постоянным.

Эти проблемы называются податливыми , в то время как другие называются неразрешимыми или суперполиномиальными .

Формально алгоритм является алгоритмом полиномиального времени, если существует такой многочлен p (n) , что алгоритм может решить любой экземпляр размера n за время O (p (n)) .

Задача, требующая времени Ω (n ⁵⁰ ), по существу неразрешима для больших n . Наиболее известный алгоритм полиномиального времени выполняется во времени O (n ^k ) для достаточно низкого значения k .

Преимущества в рассмотрении класса алгоритмов полиномиального времени заключаются в том, что все разумные детерминированные однопроцессорные модели вычислений могут быть смоделированы друг на друге с максимальным полиномиальным

NP-класс

Класс NP состоит из тех задач, которые проверяемы за полиномиальное время. NP — это класс проблем решения, для которого легко проверить правильность заявленного ответа с помощью небольшой дополнительной информации. Следовательно, мы не просим найти способ найти решение, а только для проверки того, что предполагаемое решение действительно является правильным.

Каждая проблема в этом классе может быть решена в экспоненциальном времени с помощью исчерпывающего поиска.

P против NP

Каждая задача решения, которая разрешима детерминированным алгоритмом полиномиального времени, также разрешима недетерминированным алгоритмом полиномиального времени.

Все проблемы в P могут быть решены с помощью алгоритмов полиномиального времени, тогда как все проблемы в NP — P неразрешимы.

Не известно, является ли P = NP . Однако в NP известны многие проблемы со свойством, что если они принадлежат P, то можно доказать, что P = NP.

Если P ≠ NP , то в NP есть проблемы, которых нет ни в P, ни в NP-Complete.

Задача принадлежит классу P, если ее легко найти решение. Проблема принадлежит NP , если легко проверить решение, которое, возможно, было очень утомительным.

DAA — теорема Кука

Стивен Кук представил четыре теоремы в своей статье «Сложность процедур доказательства теорем». Эти теоремы изложены ниже. Мы понимаем, что в этой главе используются многие неизвестные термины, но у нас нет возможности обсуждать все подробно.

Ниже приведены четыре теоремы Стивена Кука:

Теорема-1

Если набор S строк принят некоторой недетерминированной машиной Тьюринга в течение полиномиального времени, то S сводится к P к {тавтологиям DNF}.

Теорема-2

Следующие множества P-сводимы друг к другу в парах (и, следовательно, каждый имеет одинаковую полиномиальную степень сложности): {тавтологии}, {тавтологии DNF}, D3, {пары подграфов}.

Теорема-3

• Для любого T _Q (k) типа Q $\ mathbf {\ frac {T_ {Q} (k)} {\ frac {\ sqrt {k}} {(log \: k) ^ 2}}}$ $ неограниченный

• Существует T _Q (k) типа Q такой, что $T_ {Q} (k) \ leqslant 2 ^ {k (log \: k) ^ 2}$

Для любого T _Q (k) типа Q $\ mathbf {\ frac {T_ {Q} (k)} {\ frac {\ sqrt {k}} {(log \: k) ^ 2}}}$ $ неограниченный

Существует T _Q (k) типа Q такой, что $T_ {Q} (k) \ leqslant 2 ^ {k (log \: k) ^ 2}$

Теорема-4

Если множество строк S принимается недетерминированной машиной в течение времени T (n) = 2 ⁿ , и если T _Q (k) является честной (то есть счетной в реальном времени) функцией типа Q , то существует постоянная K , поэтому S может быть распознан детерминированной машиной за время T _Q (K8 ⁿ ) .

• Во-первых, он подчеркнул важность полиномиальной временной сводимости. Это означает, что если мы имеем сокращение полиномиального времени от одной задачи к другой, это гарантирует, что любой алгоритм полиномиального времени из второй задачи может быть преобразован в соответствующий алгоритм полиномиального времени для первой задачи.

• Во-вторых, он акцентировал внимание на классе NP задач решения, которые могут быть решены за полиномиальное время с помощью недетерминированного компьютера. Большинство неразрешимых проблем относятся к этому классу NP.

• В-третьих, он доказал, что одна конкретная проблема в NP обладает тем свойством, что любая другая проблема в NP может быть полиномиально сведена к нему. Если проблема выполнимости может быть решена с помощью алгоритма полиномиального времени, то любая задача в NP также может быть решена за полиномиальное время. Если любая проблема в NP неразрешима, то проблема выполнимости должна быть неразрешимой. Таким образом, проблема выполнимости является самой сложной проблемой в NP.

• В-четвертых, Кук предположил, что другие проблемы в NP могут быть связаны с проблемой удовлетворенности этим свойством быть самым твердым членом NP.

Во-первых, он подчеркнул важность полиномиальной временной сводимости. Это означает, что если мы имеем сокращение полиномиального времени от одной задачи к другой, это гарантирует, что любой алгоритм полиномиального времени из второй задачи может быть преобразован в соответствующий алгоритм полиномиального времени для первой задачи.

Во-вторых, он акцентировал внимание на классе NP задач решения, которые могут быть решены за полиномиальное время с помощью недетерминированного компьютера. Большинство неразрешимых проблем относятся к этому классу NP.

В-третьих, он доказал, что одна конкретная проблема в NP обладает тем свойством, что любая другая проблема в NP может быть полиномиально сведена к нему. Если проблема выполнимости может быть решена с помощью алгоритма полиномиального времени, то любая задача в NP также может быть решена за полиномиальное время. Если любая проблема в NP неразрешима, то проблема выполнимости должна быть неразрешимой. Таким образом, проблема выполнимости является самой сложной проблемой в NP.

В-четвертых, Кук предположил, что другие проблемы в NP могут быть связаны с проблемой удовлетворенности этим свойством быть самым твердым членом NP.

NP Hard и NP-Complete Классы

Проблема в классе NPC, если она в NP и такая же сложная, как любая проблема в NP. Проблема является NP-трудной, если все проблемы в NP сводятся к ней за полиномиальное время, даже если она не может быть в самой NP.

Если для любой из этих задач существует алгоритм полиномиального времени, все задачи в NP будут решаться за полиномиальное время. Эти проблемы называются NP-полными . Феномен NP-полноты важен как по теоретическим, так и по практическим причинам.

Определение NP-полноты

Язык B является NP-полным, если он удовлетворяет двум условиям

• Б находится в НП

• Каждое A в NP является полиномиальным временем, приводимым к B.

Б находится в НП

Каждое A в NP является полиномиальным временем, приводимым к B.

Если язык удовлетворяет второму свойству, но не обязательно первому, язык B называется NP-Hard . Неформально, проблема поиска B является NP-трудной, если существует некоторая NP-полная проблема A, которую Тьюринг сводит к B.

Проблема в NP-Hard не может быть решена за полиномиальное время, пока P = NP . Если проблема оказывается NPC, нет необходимости тратить время на поиск эффективного алгоритма для нее. Вместо этого мы можем сосредоточиться на алгоритме аппроксимации дизайна.

NP-полные задачи

Ниже приведены некоторые задачи NP-Complete, для которых не известен алгоритм полиномиального времени.

• Определение, имеет ли граф гамильтонов цикл
• Определение того, является ли булева формула выполнимой и т. Д.

NP-сложные проблемы

Следующие проблемы являются NP-Hard

• Проблема выполнимости схемы
• Установить обложку
• Вершинное покрытие
• Задача коммивояжера

В этом контексте, теперь мы обсудим TSP является NP-Complete

TSP является NP-Complete

Задача коммивояжера состоит из коммивояжера и множества городов. Продавец должен посетить каждый из городов, начиная с определенного и возвращаясь в тот же город. Проблема в том, что коммивояжёр хочет минимизировать общую длину поездки.

доказательство

Чтобы доказать, что TSP является NP-Complete , сначала мы должны доказать, что TSP принадлежит NP . В TSP мы находим тур и проверяем, что тур содержит каждую вершину один раз. Затем рассчитывается общая стоимость краев тура. Наконец, мы проверяем, является ли стоимость минимальной. Это может быть выполнено за полиномиальное время. Таким образом, TSP принадлежит NP .

Во-вторых, мы должны доказать, что TSP NP-сложен . Чтобы доказать это, можно показать, что гамильтонов цикл ≤ _p TSP (поскольку мы знаем, что задача о гамильтоновом цикле NP-полна).

Предположим, что G = (V, E) является экземпляром гамильтонова цикла.

Следовательно, экземпляр TSP построен. Создаем полный граф G ^‘ = (V, E ^‘ ) , где

$$E ^ {'} = \ lbrace (i, j) \ двоеточие i, j \ in V \: \: и \: i \ neq j$$

Таким образом, функция стоимости определяется следующим образом:

$$t (i, j) = \ begin {case} 0 &amp;amp; if \: (i, j) \: \ in E \\ 1 &amp;amp; в противном случае \ end {case}$$

Предположим теперь, что в G существует гамильтонов цикл. Ясно, что стоимость каждого ребра в h равна 0 в G ^‘, поскольку каждое ребро принадлежит E. Следовательно, h имеет стоимость 0 в G ^‘ . Таким образом, если у графа G есть гамильтонов цикл, то у графа G ^‘ тур 0 стоимости.

И наоборот, мы предполагаем, что G ^‘ имеет тур h ^‘ стоимости не более 0 . Стоимость ребер в E ^‘ равна 0 и 1 по определению. Следовательно, каждое ребро должно иметь стоимость 0, поскольку стоимость h ^‘ равна 0 . Поэтому мы заключаем, что h ^‘ содержит только ребра в E.

Таким образом, мы доказали, что G имеет гамильтонов цикл, если и только если G ^‘ имеет обход стоимости не более 0 . TSP является NP-полной.

DAA — алгоритм восхождения на холм

Алгоритмы, обсуждаемые в предыдущих главах, работают систематически. Для достижения цели необходимо сохранить один или несколько ранее исследованных путей к решению, чтобы найти оптимальное решение.

Для многих проблем путь к цели не имеет значения. Например, в задаче N-Queens нам не нужно заботиться об окончательной конфигурации ферзей, а также о том, в каком порядке добавляются ферзьки.

Скалолазание

Hill Climbing — это метод решения определенных задач оптимизации. В этом методе мы начинаем с неоптимального решения, и решение многократно улучшается, пока какое-либо условие не будет максимизировано.

Идея начать с неоптимального решения сравнивается с началом у основания холма, улучшение решения сравнивается с подъемом по склону, и, наконец, максимизация некоторого условия сравнивается с достижением вершины холма.

Следовательно, технику восхождения на холм можно рассматривать как следующие этапы:

• Построение неоптимального решения, соблюдая ограничения задачи
• Улучшение решения шаг за шагом
• Улучшение решения до тех пор, пока улучшение не станет возможным

Техника Hill Climbing в основном используется для решения сложных вычислительных задач. Это смотрит только на текущее состояние и ближайшее будущее состояние. Следовательно, этот метод является эффективным для памяти, поскольку он не поддерживает дерево поиска.

Algorithm: Hill Climbing 
Evaluate the initial state. 
Loop until a solution is found or there are no new operators left to be applied: 
   - Select and apply a new operator 
   - Evaluate the new state: 
      goal -→ quit 
      better than current state -→ new current state 

Итеративное улучшение

В методе итеративного улучшения оптимальное решение достигается путем продвижения к оптимальному решению на каждой итерации. Тем не менее, эта техника может встретить локальные максимумы. В этой ситуации нет соседнего государства для лучшего решения.

Этой проблемы можно избежать разными способами. Одним из таких методов является моделируемый отжиг.

Случайная перезагрузка

Это еще один метод решения задачи локальных оптимумов. Эта техника проводит серию поисков. Каждый раз он начинается со случайно сгенерированного начального состояния. Следовательно, оптимальное или почти оптимальное решение может быть получено путем сравнения решений выполненных поисков.

Проблемы техники скалолазания

Местные максимы

Если эвристика не выпуклая, Hill Climbing может сходиться к локальным максимумам вместо глобальных максимумов.

Хребты и Аллеи

Если целевая функция создает узкий гребень, то альпинист может только подняться на гребень или спуститься по переулку зигзагообразно. В этом сценарии альпинист должен сделать очень маленькие шаги, требующие больше времени для достижения цели.

Плато

Плато встречается, когда область поиска является плоской или достаточно плоской, чтобы значение, возвращаемое целевой функцией, было неотличимо от значения, возвращаемого для соседних регионов, из-за точности, используемой машиной для представления ее значения.

Сложность Техники Скалолазания

Эта техника не страдает от проблем, связанных с космосом, поскольку она смотрит только на текущее состояние. Ранее исследованные пути не сохраняются.

Для большинства проблем в методе случайного перезапуска Hill Climbing оптимальное решение может быть достигнуто за полиномиальное время. Однако для задач NP-Complete вычислительное время может быть экспоненциальным в зависимости от количества локальных максимумов.

Применение техники скалолазания

Техника Hill Climbing может быть использована для решения многих проблем, где текущее состояние позволяет выполнять точную функцию оценки, такую ​​как Network-Flow, задача коммивояжера, задача 8 Queens, проектирование интегральной микросхемы и т. Д.

Скалолазание также используется в индуктивных методах обучения. Эта техника используется в робототехнике для координации действий нескольких роботов в команде. Есть много других проблем, где этот метод используется.

пример

Эта техника может быть применена для решения проблемы коммивояжера. Сначала определяется первоначальное решение, которое посещает все города ровно один раз. Следовательно, это начальное решение не является оптимальным в большинстве случаев. Даже это решение может быть очень плохим. Алгоритм Hill Climbing начинается с такого начального решения и вносит в него улучшения итеративным способом. В конце концов, гораздо более короткий путь может быть получен.