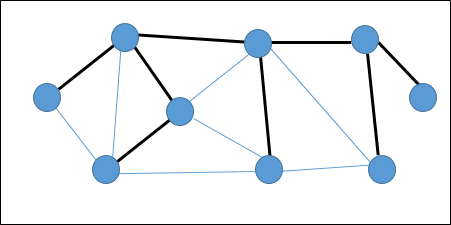
Связующее дерево — это подмножество неориентированного графа, в котором все вершины связаны минимальным числом ребер.
Если все вершины связаны в графе, то существует хотя бы одно остовное дерево. На графике может существовать более одного связующего дерева.
свойства
- У остовного дерева нет цикла.
- Любая вершина может быть достигнута из любой другой вершины.
пример
На следующем графике выделенные ребра образуют остовное дерево.
Минимальное остовное дерево
Минимальное связующее дерево (MST) — это подмножество ребер связного взвешенного неориентированного графа, который соединяет все вершины вместе с минимально возможным общим весом ребер. Чтобы получить MST, можно использовать алгоритм Прима или алгоритм Крускала. Следовательно, мы обсудим алгоритм Прима в этой главе.
Как мы уже обсуждали, один граф может иметь более одного связующего дерева. Если имеется n вершин, связующее дерево должно иметь n — 1 число ребер. В этом контексте, если каждое ребро графа связано с весом и существует более одного остовного дерева, нам нужно найти минимальное остовное дерево графа.
Кроме того, если существуют дублированные взвешенные ребра, граф может иметь несколько минимальных остовных деревьев.
На приведенном выше графике мы показали связующее дерево, хотя это не минимальное остовное дерево. Стоимость этого связующего дерева (5 + 7 + 3 + 3 + 5 + 8 + 3 + 4) = 38.
Мы будем использовать алгоритм Прима, чтобы найти минимальное остовное дерево.
Алгоритм Прима
Алгоритм Прима — это жадный подход к поиску минимального остовного дерева. В этом алгоритме, чтобы сформировать MST, мы можем начать с произвольной вершины.
Algorithm: MST-Prim’s (G, w, r)
for each u є G.V
u.key = ∞
u.∏ = NIL
r.key = 0
Q = G.V
while Q ≠ Ф
u = Extract-Min (Q)
for each v є G.adj[u]
if each v є Q and w(u, v) < v.key
v.∏ = u
v.key = w(u, v)
Функция Extract-Min возвращает вершину с минимальной стоимостью ребра. Эта функция работает на минимальной куче.
пример
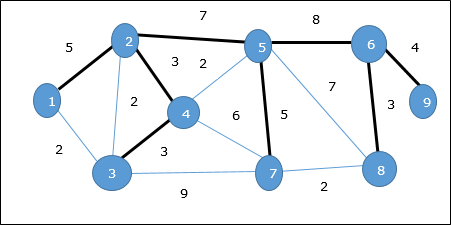
Используя алгоритм Прима, мы можем начать с любой вершины, начнем с вершины 1 .
Вершина 3 соединяется с вершиной 1 с минимальной стоимостью ребра, поэтому ребро (1, 2) добавляется в остовное дерево.
Далее рассматривается ребро (2, 3), так как это минимум среди ребер {(1, 2), (2, 3), (3, 4), (3, 7)} .
На следующем шаге мы получаем ребро (3, 4) и (2, 4) с минимальными затратами. Край (3, 4) выбирается случайным образом.
Аналогичным образом выбираются ребра (4, 5), (5, 7), (7, 8), (6, 8) и (6, 9) . Поскольку все вершины посещены, алгоритм останавливается.
Стоимость связующего дерева составляет (2 + 2 + 3 + 2 + 5 + 2 + 3 + 4) = 23. В этом графе больше нет связующего дерева со стоимостью менее 23 .