Ранее мы исследовали подход с использованием векторных областей для реализации поля зрения турели. Войска подошли к башне на открытом поле, и между ними не было никаких препятствий. Теперь предположим, что есть препятствие, скажем, стена, которая заслоняет видимость отряда с башни; как мы должны это реализовать? Этот учебник предлагает подход к решению этой проблемы.
Окончательный результат предварительного просмотра
Давайте посмотрим на конечный результат, к которому мы будем стремиться. Нажмите на башню в нижней части сцены, чтобы начать симуляцию.
Шаг 1: Основная концепция
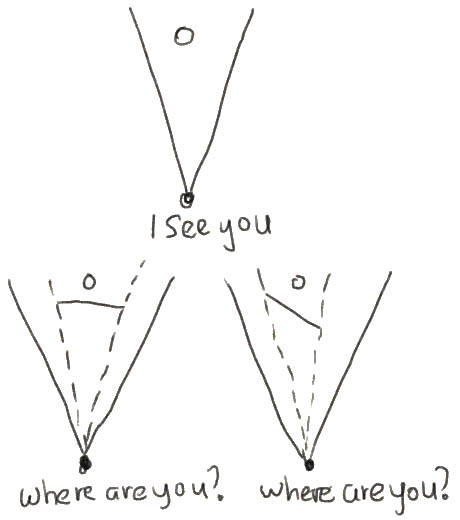
Вот что мы пытаемся достичь в этом уроке. Посмотрите на изображение выше. Башня может видеть воинское подразделение, если оно находится в поле зрения башни (вверху). Как только мы поместим стену между башней и солдатом, видимость солдата будет закрыта от башни.
Шаг 2: Резюме
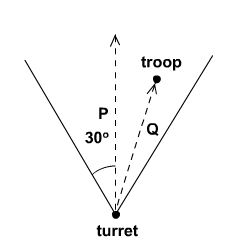
Прежде всего, давайте сделаем небольшую ревизию. Скажем, вектор линии визирования башни равен P, а вектор от башни к солдату — Q. Солдат виден башне, если:
- Угол между P и Q меньше угла зрения (в данном случае 30 ° с обеих сторон)
- Величина P больше Q
Шаг 3: Обзор подхода

Выше приведен псевдокод для подхода, который мы предпримем. Определение того, находится ли солдат в поле зрения башни (FOV), объясняется на шаге 2. Теперь давайте перейдем к определению, находится ли солдат за стеной.
Мы будем использовать векторные операции для достижения этой цели. Я уверен, что после упоминания об этом быстро приходят в голову точечные и перекрестные произведения Мы сделаем небольшой обход для пересмотра этих двух векторных операций, чтобы убедиться, что каждый может следовать.
Шаг 4: Точка и перекрестный продукт между векторами
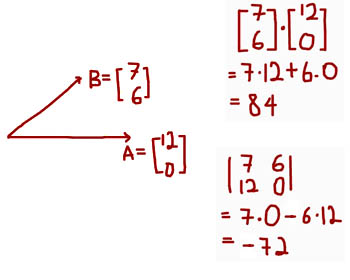
Давайте вернемся к векторным операциям: точечный продукт и перекрестный продукт. Это не класс по математике, и мы рассмотрели их более подробно ранее, но все же хорошо освежить нашу память о работе, поэтому я включил изображение выше. Диаграмма показывает операцию «B точка A» (верхний правый угол) и операцию «B крест A» (нижний правый угол).
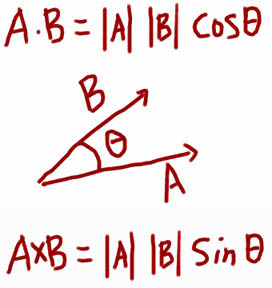
Более важными являются уравнения этих операций. Посмотрите на изображение ниже. |A| и |B| обратитесь к скалярной величине каждого вектора — длине стрелки. Обратите внимание, что скалярное произведение относится к косинусу угла между векторами, а перекрестное произведение относится к синусу угла между векторами.
Шаг 5: синус и косинус
Далее в тему тригонометрии: синус и косинус. Я уверен, что эти графики разжигают теплые воспоминания (или муки). Для просмотра графиков с разными единицами (градусы или радианы) нажимайте кнопки на представлении Flash ниже.
Обратите внимание, что эти формы волны являются непрерывными и повторяющимися. Например, вы можете вырезать и вставить синусоидальную волну в отрицательный диапазон, чтобы получить что-то вроде ниже.
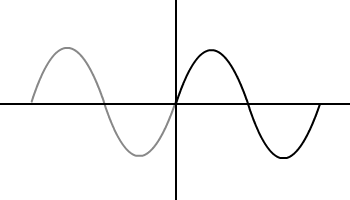
Шаг 6: Сводка ценностей
| степень | Синус степени | Косинус степени |
| -180 | 0 | -1 |
| -90 | -1 | 0 |
| 0 | 0 | 1 |
| 90 | 1 | 0 |
| 180 | 0 | -1 |
В таблице выше показаны значения косинуса и синуса, соответствующие определенным градусам. Вы заметите, что положительный синус-график охватывает диапазон от 0 ° до 180 °, а положительный косинус-график охватывает от -90 ° до 90 °. Мы свяжем эти значения с точечным произведением и перекрестным произведением позже.
Шаг 7: Геометрическая интерпретация точечного продукта
Так как все это может быть полезно? Чтобы перейти к погоне, скалярное произведение является мерой того, насколько параллельны векторы, тогда как перекрестное произведение является мерой того, насколько ортогональны векторы.
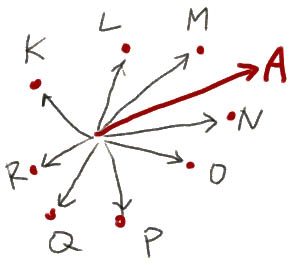
Давайте сначала разберемся с точечным произведением. Вспомните формулу для точечного произведения, как упоминалось в шаге 4. Мы можем определить, является ли результат положительным или отрицательным, просто посмотрев на косинус угла, зажатого между двумя векторами. Почему? Потому что величина вектора всегда положительна. Единственным оставшимся параметром, определяющим знак результата, является косинус угла.
Опять же, напомним, что положительный косинус-график охватывает -90 ° — 90 °, как на шаге 6. Следовательно, скалярное произведение A с любым из указанных выше векторов L, M, N, O будет давать положительное значение, поскольку угол заклинивает между А и любым из этих векторов находится в пределах от -90 ° до 90 °! (Чтобы быть точным, положительный диапазон больше похож на -89 ° — 89 °, потому что и -90 °, и 90 ° дают значения косинуса 0, что приводит нас к следующей точке.) Точечное произведение между A и P (задано P перпендикулярно А) будет производить 0. Остальное, я думаю, вы уже можете догадаться: скалярное произведение А с К, R или Q будет давать отрицательное значение.
Используя точечное произведение, мы можем разделить область на нашей сцене на две области. Точечное произведение вектора ниже с любой точкой, которая находится внутри области, помеченной «х», будет давать положительное значение, тогда как точечное произведение с точками в области, помеченной «о», будет давать отрицательные значения.

Шаг 8: Геометрическая интерпретация перекрестного продукта
Давайте перейдем к перекрестному произведению. Помните, что перекрестное произведение относится к синусу угла, зажатого между двумя векторами. Положительный синусоидальный график охватывает диапазон от 0 ° до 180 °; отрицательный диапазон охватывает от 0 ° до -180 °. Изображение ниже суммирует эти моменты.
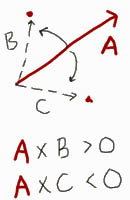
Итак, если посмотреть еще раз на диаграмму из шага 7, перекрестное произведение между A и K, L или M будет давать положительные значения, в то время как перекрестное произведение между A и N, O, P или Q будет давать отрицательные значения. Перекрестное произведение между A и R даст 0, так как синус 180 ° равен 0.
Чтобы пояснить далее, перекрестное произведение вектора между любой точкой, которая находится в области, помеченной буквой «о», ниже, будет положительным, тогда как в области, помеченной знаком «х», будет отрицательным.

Следует отметить, что в отличие от точечного произведения, перекрестное произведение чувствительно к последовательности. Это означает, что результаты BxA и BxA будут разными с точки зрения направления. Поэтому, когда мы пишем нашу программу, мы должны быть точными при выборе вектора для сравнения.
(Примечание. Эти объяснения применимы к двумерному декартову пространству.)
Шаг 9: Демо-приложение
Чтобы укрепить ваше понимание, я разместил здесь небольшое приложение, чтобы вы могли поиграть. Нажмите на синий шар в верхней части сцены и перетащите его. При перемещении значение текстового поля будет обновляться в зависимости от выбранной операции (точка или перекрестное произведение между статической стрелкой и той, которую вы контролируете).
Вы можете наблюдать одну странность с перевернутым направлением перекрестного произведения. Верхняя область отрицательная, а нижняя положительная, в отличие от нашего объяснения на предыдущем шаге. Что ж, это связано с тем, что ось Y инвертирована в координатном пространстве Flash по сравнению с декартовым координатным пространством; это указывает вниз, тогда как традиционно математики принимают это как указывающее вверх.
Шаг 10: Определение регионов
Теперь, когда вы поняли концепцию регионов, давайте немного потренируемся. Мы разделим наше пространство на четыре квадранта: A1, A2, B1, B2.
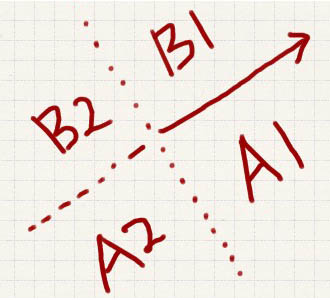
Я свел в таблицу результаты, чтобы проверить ниже. «Вектор» здесь относится к стрелке на изображении выше. «Точка» относится к любой координате в указанной области. Вектор делит сцену на четыре основные области, где разделители (пунктирные линии) простираются до бесконечности.
| Область | Вектор на диаграмме перекрестного произведения с точкой | Вектор на диаграмме точка продукта с точкой |
| A1 | (+), из-за координатного пространства Flash | (+) |
| A2 | (+) | (-) |
| B1 | (-) из-за координатного пространства Flash | (+) |
| Би 2 | (-) | (-) |
Шаг 11: Разделение регионов
Вот презентация Flash, демонстрирующая идеи, описанные в шаге 10. Щелкните правой кнопкой мыши по сцене, чтобы открыть контекстное меню, и выберите регион, который вы хотите выделить.
Шаг 12: Реализация
Вот реализация ActionScript концепции, описанной в шаге 10. Не стесняйтесь просматривать весь фрагмент кода в исходной загрузке, как AppLine.as .
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
//highlighting color according to user selection
private function color():void
{
//each ball on stage is checked against conditions for selected case
for each (var item:Ball in sp)
{
var vec1:Vector2D = new Vector2D(item.x — stage.stageWidth * 0.5, item.y — stage.stageHeight * 0.5);
if (select == 0) {
if (vec.vectorProduct(vec1) > 0) item.col = 0xFF9933;
else item.col = 0x334455;
}
else if (select == 1){
if (vec.dotProduct(vec1) > 0) item.col = 0xFF9933;
else item.col = 0x334455;
}
else if (select == 2){
if (vec.vectorProduct(vec1) > 0 && vec.dotProduct(vec1) > 0) item.col = 0xFF9933;
else item.col = 0x334455;
}
else if (select == 3){
if (vec.vectorProduct(vec1) > 0 &&vec.dotProduct(vec1) <0) item.col = 0xFF9933;
else item.col = 0x334455;
}
else if (select == 4){
if (vec.vectorProduct(vec1) < 0 &&vec.dotProduct(vec1) > 0) item.col = 0xFF9933;
else item.col = 0x334455;
}
else if (select == 5){
if (vec.vectorProduct(vec1) < 0 &&vec.dotProduct(vec1) < 0) item.col = 0xFF9933;
else item.col = 0x334455;
}
item.draw();
}
}
//swapping case according to user selction
private function swap(e:ContextMenuEvent):void
{
if (e.target.caption == «VectorProduct») select = 0;
else if (e.target.caption == «DotProduct») select = 1;
else if (e.target.caption == «RegionA1») select = 2;
else if (e.target.caption == «RegionA2») select = 3;
else if (e.target.caption == «RegionB1») select = 4;
else if (e.target.caption == «RegionB2») select = 5;
}
|
Шаг 13: Экранированная видимость
Поняв геометрические интерпретации точечного произведения и перекрестного произведения, мы применим его к нашему сценарию. Представленная выше флэш-презентация показывает варианты того же сценария и суммирует условия, применяемые к солдату, защищенному стеной, но находящейся внутри поля зрения башни. Вы можете прокручивать кадры с помощью кнопок со стрелками.
Следующие объяснения основаны на координатном пространстве 2D Flash. В кадре 1 стена установлена между башенкой и солдатом. Пусть A и B будут векторами от башни до хвоста и головы вектора стены соответственно. Пусть C — вектор стены, а D — вектор от хвоста стены до солдата. Наконец, пусть Q будет вектором от башни до солдата.
Я привел в таблицу полученные условия ниже.
| Место расположения | Перекрестный продукт |
| Отряд перед стеной | C x D> 0 |
| Отряд за стеной | C x D |
Это не единственное применимое условие, потому что мы также должны ограничить военнослужащего в пределах пунктирных линий с обеих сторон. Проверьте кадры 2-4, чтобы увидеть следующий набор условий.
| Место расположения | Перекрестный продукт |
| Отряд находится по бокам стены. | Q x A 0 |
| Отряд слева от стены | Q x A> 0, Q x B> 0 |
| Отряд справа от стены | Q x A |
Я думаю, что мои коллеги-читатели теперь могут выбрать подходящие условия, чтобы определить, скрыт ли солдат в поле зрения или нет. Имейте в виду, что этот набор условий оценивается после того, как мы обнаружили, что отряд находится в поле зрения башни (см. Шаг 3).
Шаг 14: Реализация ActionScript
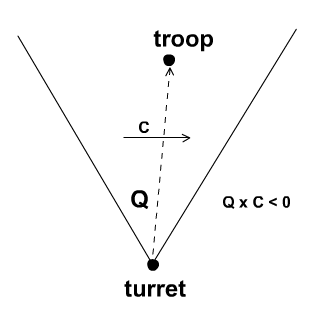
Вот реализация ActionScript концепций, объясненных на шаге 13. На изображении выше показан начальный вектор стены, C. Нажмите и перетащите красную кнопку внизу и переместите ее вокруг, чтобы увидеть экранированную область. Вы можете просмотреть полный исходный код в HiddenSector.as .
Хорошо, я надеюсь, что вы экспериментировали с красным шаром, и если вы достаточно наблюдательны, вы могли заметить ошибку. Обратите внимание, что область не экранирована, поскольку красная кнопка перемещается влево от другого конца стены, таким образом, инвертируя вектор стены, чтобы он указывал налево, а не вправо. Решение в следующем шаге.
Однако перед этим давайте рассмотрим важный фрагмент ActionScript здесь, в HiddenSector.as :
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
private function highlight():void {
var lineOfSight:Vector2D = new Vector2D(0, -50)
var sector:Number = Math2.radianOf(30);
for each (var item:Ball in sp) {
var turret_sp:Vector2D = new Vector2D(item.x — turret.x, item.y — turret.y);
if (Math.abs(lineOfSight.angleBetween(turret_sp)) < sector) {
var wall:Vector2D = new Vector2D(wall2.x — wall1.x, wall2.y — wall1.y);
var turret_wall1:Vector2D = new Vector2D(wall1.x — turret.x, wall1.y — turret.y);
var turret_wall2:Vector2D = new Vector2D(wall2.x — turret.x, wall2.y — turret.y);
var wall_sp:Vector2D = new Vector2D (item.x — wall1.x, item.y — wall1.y);
if ( wall.vectorProduct (wall_sp) < 0 // C x D
&& turret_sp.vectorProduct(turret_wall1) < 0 // Q x A
&& turret_sp.vectorProduct(turret_wall2) > 0 // Q x B
) { item.col = 0xcccccc }
else { item.col = 0;
item.draw();
}
}
}
|
Шаг 15: Направление стены
Чтобы решить эту проблему, нам нужно знать, направлен ли вектор стены влево или вправо. Допустим, у нас есть опорный вектор R, который всегда указывает вправо.
| Направление вектора | Скалярное произведение |
| Стена направлена вправо (с той же стороны, что и R) | с R> 0 |
| Стена указывает налево (противоположная сторона R) | с р |
Конечно, есть и другие способы решения этой проблемы, но я полагаю, что это возможность использовать концепции, изложенные в этом руководстве, так что все готово.
Шаг 16: твики Actionscript
Ниже представлена презентация Flash, в которой реализовано исправление, описанное в шаге 15. После того, как вы поиграете с ним, прокрутите вниз, чтобы проверить настройки ActionScript.
Изменения по сравнению с предыдущей реализацией выделены. Кроме того, наборы условий переопределяются в соответствии с направлением стены:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
private function highlight():void {
var lineOfSight:Vector2D = new Vector2D(0, -50);
var sector:Number = Math2.radianOf(30);
var pointToRight:Vector2D = new Vector2D(10, 0);
for each (var item:Ball in sp) {
var turret_sp:Vector2D = new Vector2D(item.x — turret.x, item.y — turret.y);
if (Math.abs(lineOfSight.angleBetween(turret_sp)) < sector) {
var wall:Vector2D = new Vector2D(wall2.x — wall1.x, wall2.y — wall1.y);
var turret_wall1:Vector2D = new Vector2D(wall1.x — turret.x, wall1.y — turret.y);
var turret_wall2:Vector2D = new Vector2D(wall2.x — turret.x, wall2.y — turret.y);
var wall_sp:Vector2D = new Vector2D (item.x — wall1.x, item.y — wall1.y);
var sides: Boolean;
if (pointToRight.dotProduct(wall) > 0) {
sides = wall.vectorProduct (wall_sp) < 0 // C x D
&& turret_sp.vectorProduct(turret_wall1) < 0 // Q x A
&& turret_sp.vectorProduct(turret_wall2) > 0 // Q x B
}
else {
sides = wall.vectorProduct (wall_sp) > 0 // C x D
&& turret_sp.vectorProduct(turret_wall1) > 0 // Q x A
&& turret_sp.vectorProduct(turret_wall2) < 0 // Q x B
}
if (sides) { item.col = 0xcccccc }
else { item.col = 0;
item.draw();
}
}
}
|
Проверьте полный источник в HiddenSector2.as .
Шаг 17: Настройте стену
Теперь мы Scene1.as нашу работу на Scene1.as из предыдущего урока. Сначала мы установим нашу стену.
Мы инициируем переменные,
|
1
2
3
4
5
6
7
|
public class Scene1_2 extends Sprite
{
private var river:Sprite;
private var wall_origin:Vector2D, wall:Vector2D;
private var troops:Vector.<Ball>;
private var troopVelo:Vector.<Vector2D>;
|
… затем нарисуйте стену в первый раз,
|
01
02
03
04
05
06
07
08
09
10
|
public function Scene1_2() {
makeTroops();
makeRiver();
makeWall();
makeTurret();
turret.addEventListener(MouseEvent.MOUSE_DOWN, start);
function start ():void {
stage.addEventListener(Event.ENTER_FRAME, move);
}
}
|
|
1
2
3
4
5
6
|
private function makeWall():void {
wall_origin = new Vector2D(200, 260);
graphics.lineStyle(2, 0);
graphics.moveTo(wall_origin.x, wall_origin.y);
graphics.lineTo(wall_origin.x + wall.x , wall_origin.y+wall.y);
}
|
… и перерисовывать каждый кадр, потому что вызов graphics.clear() находится где-то в behaviourTurret() :
|
1
2
3
4
5
6
|
//added in 2nd tutorial
private function move(e:Event):void {
behaviourTroops();
behaviourTurret();
redrawWall();
}
|
|
1
2
3
4
5
6
|
//added in second tutorial
private function redrawWall():void {
graphics.lineStyle(2, 0);
graphics.moveTo(wall_origin.x, wall_origin.y);
graphics.lineTo(wall_origin.x + wall.x , wall_origin.y+wall.y);
}
|
Шаг 18: Взаимодействие со Стеной
Войска также будут взаимодействовать со стеной. Когда они сталкиваются со стеной, они будут скользить вдоль стены. Я не буду пытаться вдаваться в подробности этого, так как это подробно описано в « Столкновительной реакции между кругом и отрезком линии» . Я призываю читателей проверить это для дальнейшего объяснения.
Следующий фрагмент находится в функции behaviourTroops() .
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
//Version 2
//if wading through river, slow down
//if collide with wall, slide through
//else normal speed
var collideWithRiver:Boolean = river.hitTestObject(troops[i])
var wall_norm:Vector2D = wall.rotate(Math2.radianOf( -90));
var wall12Troop:Vector2D = new Vector2D(troops[i].x — wall_origin.x, troops[i].y — wall_origin.y);
var collideWithWall:Boolean = troops[i].rad > Math.abs(wall12Troop.projectionOn(wall_norm))
&& wall12Troop.getMagnitude() < wall.getMagnitude()
&& wall12Troop.dotProduct(wall) > 0;
if (collideWithRiver) troops[i].y += troopVelo[i].y*0.3;
else if (collideWithWall) {
//reposition troop
var projOnNorm:Vector2D = wall_norm.normalise();
var projOnWall:Vector2D = wall.normalise();
projOnWall.scale(wall12Troop.projectionOn(wall));
var reposition:Vector2D = projOnNorm.add(projOnWall);
troops[i].x = wall_origin.x + reposition.x;
//slide through the wall
var adjustment:Number = Math.abs(troopVelo[i].projectionOn(wall_norm));
var slideVelo:Vector2D = wall_norm.normalise();
slideVelo = slideVelo.add(troopVelo[i])
troops[i].x += slideVelo.x;
}
else troops[i].y += troopVelo[i].y
|
Шаг 19: Проверка «скрытности» солдат
Наконец, мы подошли к сути этого урока: настройка условий и проверка, находятся ли солдаты за стеной и, следовательно, защищены от видимости башни. Я выделил важные коды исправлений:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
|
//check if enemy is within sight
//1.
//2.
//3.
var c1:Boolean = Math.abs(lineOfSight.angleBetween(turret2Item)) < Math2.radianOf(sectorOfSight) ;
var c2:Boolean = turret2Item.getMagnitude() < lineOfSight.getMagnitude();
var c3:Boolean = turret2Item.getMagnitude() < closestDistance;
//Checking whether troop is shielded by wall
var withinLeft:Boolean = turret2Item.vectorProduct(turret2wall1) < 0
var withinRight:Boolean = turret2Item.vectorProduct(turret2wall2) > 0
var behindWall:Boolean = wall.vectorProduct(wall12troop) < 0;
var shielded:Boolean = withinLeft && withinRight && behindWall
//if all conditions fulfilled, update closestEnemy
if (c1 && c2&& c3 && !shielded){
closestDistance = turret2Item.getMagnitude();
closestEnemy = item;
}
|
Проверьте полный код в Scene1_2.as .
Шаг 20: запустите приложение
Наконец, мы можем расслабиться и проверить патч в действии. Нажмите Ctrl + Enter, чтобы увидеть результаты вашей работы. Я включил копию рабочей презентации Flash ниже. Нажмите на башню в нижней части сцены, чтобы начать симуляцию.