В Развертывание танка в Изометрической зоне боевых действий вы узнали, как заставить объект вращаться, поворачиваясь лицом к указателю и перемещаясь к месту щелчка. В этом кратком совете мы рассмотрим общую математику: тригонометрию .
Окончательный результат предварительного просмотра
Это окончательный результат моего предыдущего урока. Он использует принципы тригонометрии, которые мы рассмотрим в этом кратком совете:
Переместите мышь, чтобы нацелить башню, и щелкните в любом месте, чтобы танк подъехал к этой точке.
Любой программист, особенно любой игровой программист, рано или поздно сталкивается с необходимостью перемещать объекты на экране. Это простая задача, если вам нужно переместить объект в одном направлении, например, вдоль оси x или y. Но предположим, что вы хотите, чтобы объект следовал за указателем мыши, куда бы вы его ни двигали, или создайте гоночную игру, в которой вы управляете ускорением автомобиля, нажимая клавишу со стрелкой вверх и используя стрелки влево и вправо для управления.
Допустим, вы нажимаете клавишу со стрелкой вправо один раз, и это добавляет 10 градусов к свойству поворота вашего автомобиля, но вы все равно хотите, чтобы автомобиль двигался вперед (т.е. ускорялся), когда вы нажимаете клавишу со стрелкой вверх, даже если автомобиль повернут к нижней части экран или левая или правая сторона и т. д., и вы не хотите, чтобы он выглядел так, как будто он скользит вбок. Итак, как бы вы это сделали? Вот где небольшая тригонометрия помогает!
Для тех, кто хорошо разбирается в математике, это не будет проблемой, но есть много людей, которые вообще этого не понимают или даже боятся. Я постараюсь объяснить это как можно более четко в этом кратком совете.
Шаг 1: Система координат Flash
Прежде всего, давайте вспомним декартову систему координат . Звучит сложно? Если это так, просто посмотрите на изображение ниже, и я уверен, что оно будет знакомо:
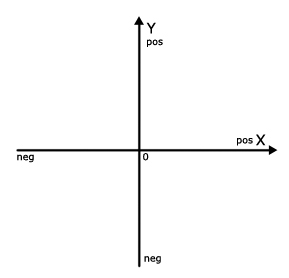
Имеет оси X и Y; Вы можете ясно видеть, где X и Y являются положительными и отрицательными. Когда дело доходит до координат во Flash, ситуация несколько иная. У Flash также есть своя система координат, но она выглядит как декартова система с ног на голову:
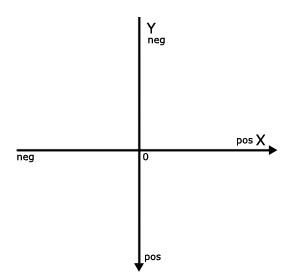
У этого также есть оси X и Y и Точка происхождения, единственное различие состоит в том, что ось Y положительна ниже оси X.
Любой символ, созданный во Flash, имеет собственную встроенную систему координат. Если вы создаете новый символ, будь то фрагмент ролика или кнопка, вы можете увидеть свойство «точки регистрации» в диалоговом окне создания символа. Что это? Точка регистрации является точкой происхождения символа. Точка, в которой объект будет вращаться, если вы измените его свойство вращения.
Примечание: исходная точка экземпляра сцены находится в левом верхнем углу. Это означает, что все точки на сцене имеют положительные координаты X и Y.
В этом кратком совете мы рассмотрим три наиболее часто используемые тригонометрические функции во Flash; Синус, Косинус и Атан2. Некоторые люди могут спросить, как мы можем использовать эти функции во Flash? Что ж, давайте посмотрим на некоторые практические примеры и поймем, зачем они нам нужны и как они могут немного облегчить нашу жизнь.
Шаг 2: Расчет угла
Давайте посчитаем угол между двумя точками. Создайте новый файл Flash (ActionScript 3.0). Выберите первый кадр на временной шкале и нажмите F9, чтобы открыть панель действий.
На этом этапе давайте сделаем что-то простое. Просто введите это в панели действий:
|
1
2
3
4
5
6
7
|
stage.addEventListener(MouseEvent.CLICK, calculateAngle)
function calculateAngle(e:MouseEvent):void
{
trace(«stage X » + e.stageX);
trace(«stage Y » + e.stageY)
}
|
Это даст нам положение указателя мыши каждый раз, когда мы щелкаем по сцене. Не совсем увлекательно, не так ли?
Хорошо, теперь предположим, что вы хотите «сообщить» некоторому объекту координаты указателя мыши относительно этого объекта, а затем показать ему направление перемещения, чтобы достичь положения указателя.
Закройте панель действий и перейдите в меню «Вставка»> «Новый символ» или просто нажмите Ctrl + F8.
Дайте ему любое имя (или оставьте имя по умолчанию) и нажмите ОК. Небольшое перекрестие в центре экрана — это точка регистрации символа или его начальная точка. Это будут позиции X и Y объекта. Теперь возьмите инструмент Oval (клавиша O) и нарисуйте круг (с нажатой клавишей Shift) в любом месте экрана.
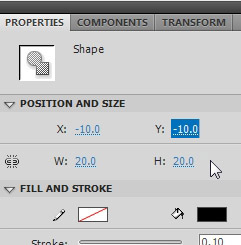
Нажмите на кружок, чтобы выбрать его, и перейдите на панель «Свойства»> «Положение и размер». Для W (ширина) введите 20, то же самое для H (высота) и для X и Y введите тип (-10). Это сделает круг размером 20х20 пикселей и точно отцентрирует его к точке регистрации. Теперь выйдите из режима редактирования символов (нажмите Сцена 1 выше), возьмите этот символ в свою библиотеку и просто перетащите его на сцену (где угодно, мы получим его положение динамически позже). Когда ваш объект окажется на сцене, mCircle ему имя экземпляра mCircle .
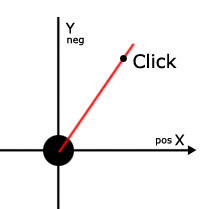
Теперь мы хотим вычислить направление от положения Y и X нашего круга до положения Y и X указателя мыши. Красная линия на изображении ниже — это направление, которое нам нужно знать. Его можно найти с помощью стандартной функции Math.atan2() .
Давай сделаем это сейчас. Удалите операторы «trace» из кода и вместо этого создайте новую переменную. Затем проследите эту переменную, чтобы увидеть, что вы получите:
|
1
2
3
4
5
6
7
8
9
|
stage.addEventListener(MouseEvent.CLICK, calculateAngle);
var myAtan2:Number;
function calculateAngle(e:MouseEvent):void
{
myAtan2 = Math.atan2(e.stageY — mCircle.y, e.stageX — mCircle.x);
trace(myAtan2);
}
|
Обратите внимание, что e.stageY - mCircle.y — это вертикальное расстояние от мыши до круга, а e.stageX - mCircle.x — это горизонтальное расстояние .
Вы будете получать эти типы чисел на панели вывода:
|
1
2
3
4
5
6
|
-2.419017353128333
3.0118660246925346
2.5704959452340326
1.6726588917423932
1.0238847495551058
0.21368467849101092
|
Это относительные углы (между линией оси X и красной линией) в радианах. Почему не градусы? Что ж, Flash использует радианы для вычисления синуса и косинуса, но если вы хотите узнать, каковы эти углы в градусах, вы всегда можете умножить «myAtan2» на 180 и разделить его на Math.PI Как это:
|
1
|
trace(myAtan2 * 180 / Math.PI) // gives you the angle in degrees;
|
Редактор: В качестве дополнительного ресурса представлен большой набор функций для преобразования градус / радиан . Он хранится в виде фрагмента на snipplr.com , последнем члене сети Envato!
Шаг 3: Понимание синуса и косинуса
Поскольку мы знаем угол между двумя точками, мы можем теперь вычислить, сколько пикселей мы должны добавить к свойствам окружности X и Y каждого кадра, пока он не достигнет точки щелчка. Давайте рассмотрим, что нам нужно знать здесь:
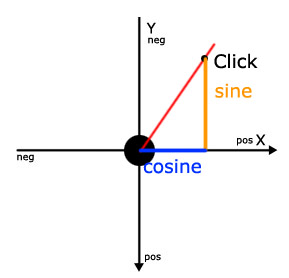
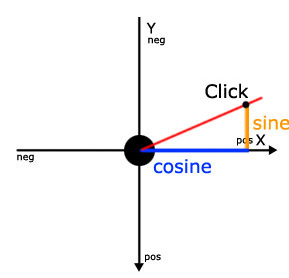
Синяя линия — это косинус угла, а оранжевая — это синус угла. Другими словами,
- Синус (угол) == e.stageY — mCircle.y
- Косинус (угол) == e.stageX — mCircle.x
Вместо того чтобы объяснить, как работают синусы и косинусы, я продемонстрирую, как их использовать, на некоторых практических примерах. Грубо говоря, синус и косинус — это отношения между Y и X в нашем ракурсе.
Представьте, что угол между двумя объектами составляет 45 градусов. В этом случае соотношение между синусом и косинусом составляет 1: 1 (см. Изображение ниже), что означает, что мы должны увеличивать свойства X и Y нашего круга на одинаковую величину каждый кадр, чтобы достичь цели. Например, вы должны добавить 5 пикселей к X и 5 пикселей к Y в каждом кадре.
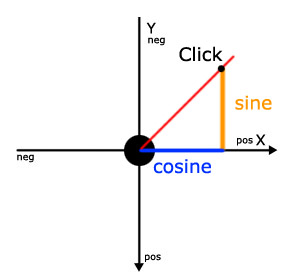
На этой диаграмме угол изменился, и отношение между синусом и косинусом также изменилось. Сейчас около 1: 2.
В этом случае мы должны добавить в два раза больше пикселей к свойству X нашего круга, чем к YEg X + = 10, Y + = 5;
Шаг 4: Практические примеры
Вы, вероятно, спросите, зачем нам синус и косинус, если мы уже знаем координаты точки щелчка — мы можем просто переместить наш mCircle к ним прямо сейчас? Ну, вы могли бы сделать это таким образом, если бы вы хотели, чтобы ваш круг (или любой другой объект) «телепортировался» в координаты точки щелчка, как только щелчок произошел. Но что, если вы хотите, чтобы он двигался постепенно в направлении щелчка? Для этого вам нужно добавить определенное количество пикселей в его свойства X и Y, например, каждый кадр или каждую секунду.
Давайте теперь посчитаем, сколько пикселей мы должны добавить к его свойствам X и Y на основе синуса и косинуса угла между нашим объектом и точкой щелчка. Помните, Flash знает угол между ними из этой операции:
|
1
|
myAtan2 = Math.atan2(e.stageY — mCircle.y, e.stageX — mCircle.x);
|
Для этого нам нужно немного обновить наш код.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
stage.addEventListener(MouseEvent.CLICK, calculateAngle);
// 2 is the maximum amount of pixels to add to the objects X and Y properties every frame
// you can use any number you like
var moveAmount:Number = 2;
var myAtan2:Number;
var mouseClickX:Number;
var mouseClickY:Number;
function calculateAngle(e:MouseEvent):void
{
mouseClickX = e.stageX;
mouseClickY = e.stageY;
myAtan2 = Math.atan2(mouseClickY — mCircle.y, mouseClickX — mCircle.x);
addEventListener(Event.ENTER_FRAME, moveTheCircle);
}
function moveTheCircle(e:Event):void
{
mCircle.x += Math.cos(myAtan2) * moveAmount;
mCircle.y += Math.sin(myAtan2) * moveAmount;
}
|
Обратите внимание на то, что я сделал здесь: я продвинул все свои переменные за пределы любых функций, потому что теперь у меня есть более одной функции, и я хочу, чтобы эти переменные были доступны из каждой функции.
|
1
2
3
4
|
var moveAmount:Number = 2;
var myAtan2:Number;
var mouseClickX:Number;
var mouseClickY:Number;
|
Этап имеет прослушиватель событий для щелчков мышью, поэтому, когда происходит щелчок, вызывается метод calculateAngle() и создаются следующие переменные:
|
1
2
3
|
mouseClickX = e.stageX;
mouseClickY = e.stageY;
myAtan2 = Math.atan2(mouseClickY — mCircle.y, mouseClickX — mCircle.x);
|
Эта функция также добавляет прослушиватель событий для moveTheCircle() кадра на сцену, который вызывает метод moveTheCircle() каждый кадр.
|
1
|
addEventListener(Event.ENTER_FRAME, moveTheCircle);
|
Шаг 5: Расчет пикселей
Теперь давайте moveTheCircle() наш moveTheCircle() . На данный момент он делает только две вещи:
|
1
2
|
mCircle.x += Math.cos(myAtan2) * moveAmount;
mCircle.y += Math.sin(myAtan2) * moveAmount;
|
Как вы можете видеть, первая строка вычисляет, сколько пикселей следует добавить к свойству X, а вторая касается Y. Позвольте мне объяснить. Math.cos находит косинус (свойство x) угла «myAtan2», Math.sin делает то же самое со своим синусом (свойство y). Если угол myAtan2 равен примерно 0,785 радиан (45 градусов), то косинус и синус будут равны примерно 0,707 … Вы можете использовать калькулятор, чтобы проверить это.
Простой расчет покажет, сколько пикселей приведенный выше код добавит к свойствам X и Y нашего объекта, если угол составляет 45 градусов.
|
1
2
3
4
5
6
|
Cosine(45 degrees) = 0.707 * 2 = 1.414;
Sine(45 degrees) = 0.707 * 2 = 1.414;
so the code will work out these results:
mCircle.x += 1.414 pixels;
mCircle.y += 1.414 pixels;
|
Если угол, например, есть. 60 градусов, тогда результаты будут такими:
|
1
2
3
4
5
6
|
Cosine(60 degrees) = 0.5 * 2 = 1;
Sine(60 degrees) = 0.866 * 2 = 1.732;
And the code would work out this way:
mCircle.x += 1 pixel;
mCircle.y += 1.732 pixels;
|
Шаг 6: Исправление проблемы с кодом
Ну, мы почти закончили. Но есть еще небольшая проблема с нашим кодом. Возможно, вы заметили, что наш объект никогда не останавливается, даже если он достигает точки щелчка, он все еще продолжает двигаться. Мы можем решить эту проблему очень легко. Когда наш объект движется к точке щелчка, расстояние между ними сокращается, поэтому абсолютное значение расстояния также уменьшается. Мы можем отслеживать это так:
|
1
2
|
trace(Math.abs(mCircle.x — mouseClickX) );
trace(Math.abs(mCircle.y — mouseClickY) );
|
( Math.abs() превращает отрицательные числа в положительные, просто умножая их на -1. Он ничего не делает с числами, которые уже положительны.)
Вам не нужно добавлять этот оператор трассировки в ваш код, я разместил его здесь, чтобы показать вам, как вы можете увидеть абсолютное значение. В этом случае оба абсолютных значения меньше 3, когда объект достигает точки щелчка. Теперь нам нужно добавить оператор if внутри нашей функции moveTheCircle() .
|
01
02
03
04
05
06
07
08
09
10
11
|
function moveTheCircle(e:Event):void
{
mCircle.x += Math.cos(myAtan2) * moveAmount;
mCircle.y += Math.sin(myAtan2) * moveAmount;
//Check if the horizontal and vertical distances from the circle to the mouse point are very close
if (Math.abs(mCircle.x — mouseClickX) < 3 && Math.abs(mCircle.y — mouseClickY) < 3)
{
removeEventListener(Event.ENTER_FRAME, moveTheCircle);
}
}
|
Когда абсолютное значение становится меньше 3, слушатель ввода кадра удаляется. Мы должны проверить абсолютные значения X и Y, потому что одно из них может достигать 3, даже если второе — нет. Это означает, что объекты могут остановиться следующим образом:
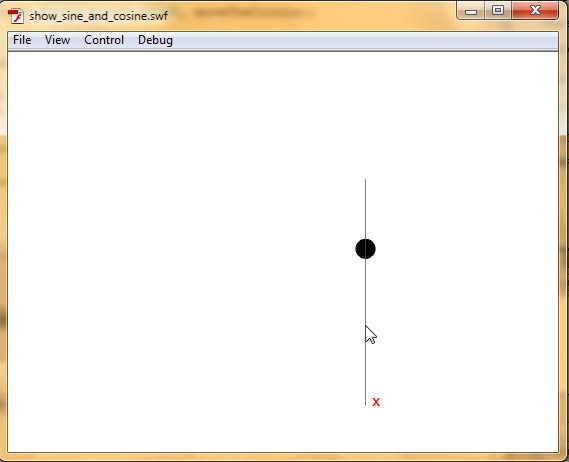
На рисунке выше показана версия, в которой проверяется только абсолютное значение X. Абсолютное значение X-расстояния уже меньше 3, поэтому оно перестало обращать внимание на значение Y.
Вывод
Ну вот и все. Я надеюсь, что этот Quick Tip поможет вам понять некоторые тригонометрии, используемые в разработке Flash 🙂