Мы рассмотрели обнаружение столкновений между бесконечной линией и кругом в нашем предыдущем кратком совете. Однако возникла проблема в том, что линия проходит дальше, чем видимый отрезок; на самом деле он распространяется на гиперплоскость. В этом кратком совете мы ограничим обнаружение столкновений только обнаружением линейного сегмента .
Окончательный результат предварительного просмотра
Мы будем работать над этим результатом:
Нажмите кнопку «Перезагрузить», чтобы изменить положение кругов в верхней части сцены.
Шаг 1: два подхода
Существует множество подходов к ограничению обнаружения столкновений в пределах отрезка. На этот раз мы рассмотрим два подхода. Первый подход немного более строг с математической точки зрения, чем второй, но это концепции, которые, если вы поймете это успешно, несомненно, принесут вам пользу в будущем. Оба подхода манипулируют характеристикой скалярного произведения, являющейся мерой того, насколько параллельны два заданных вектора.
Давайте посмотрим на первый подход. Предположим, что A и B являются векторами. Если A и B параллельны или, по крайней мере, направлены в одном направлении, то произведение точек между A и B даст положительное число. Если A и B указывают прямо напротив друг друга — или, по крайней мере, указывают в противоположных направлениях — точечный продукт между A и B будет давать отрицательное число. Если A и B ортогональны (образуя 90 ° друг к другу), то скалярное произведение даст 0.
Диаграмма ниже суммирует это описание.
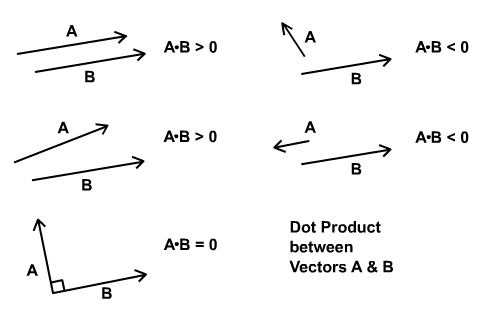
Шаг 2: связать продукт Dot с условиями
Нам нужно будет сформировать векторы B и C с обоих концов отрезка, чтобы их точечное произведение с вектором отрезка A могло определить, находится ли окружность внутри отрезка.
Соблюдайте схему ниже. Если окружность находится внутри сегмента, то значение точечного произведения между A и B является положительным, а значение между A и C — отрицательным.
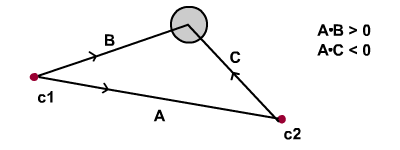
На диаграмме ниже показано, как меняется точечное произведение в зависимости от того, находится ли окружность за пределами или внутри отрезка. Обратите внимание на различия в стоимости точечного произведения.
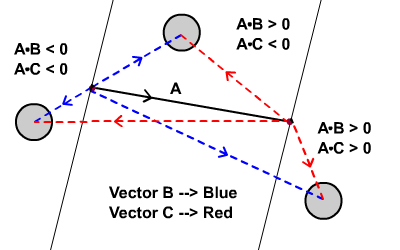
Также обратите внимание, что «внутри отрезка» не означает, что круг обязательно пересекает отрезок, просто он попадает в две тонкие линии на диаграмме выше.
Поэтому, когда происходит столкновение между линией и окружностью, как мы видели в предыдущем кратком совете , мы должны дополнительно исследовать, расположена ли окружность внутри отрезка. Если это так, то мы точно знаем, что есть подлинное пересечение.
Шаг 3: Реализация
Шаг 2 объяснил концепцию, которую мы используем, чтобы ограничить обнаружение столкновений в пределах отрезка. Однако в точности все еще есть недостаток. Видите ли, определенная область немного наклонена; мы должны стремиться использовать область, определенную согласно диаграмме ниже.
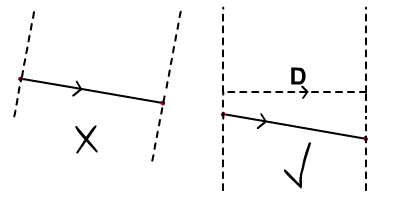
Это легко: мы просто вычисляем D как горизонтальную проекцию A. Затем, вместо того, чтобы использовать A, мы используем D, чтобы расставить точки над точками B и C. Все условия, описанные в шаге 2, остаются в силе, но вместо наклоненного сегмента. Мы определили вертикальную область.
Это исправление можно оценить визуально, если круг большой; если бы круг был маленьким, его центр был бы настолько близок к линии, что этот визуальный недостаток было бы трудно обнаружить, поэтому мы могли бы избежать использования этой слегка наклоненной области и сэкономить немного вычислительной мощности.
Тем не менее, я постараюсь сделать все правильно. Вы можете выбрать подход, слегка изменив условие.
Шаг 4: Реализация
Первый фрагмент v_line_onX здесь устанавливает вектор D ( v_line_onX )
|
1
2
3
4
|
//Att2: getting the horizontal vector
var line_onX:Number = line.projectionOn(new Vector2D(1, 0));
v_line_onX = new Vector2D(1, 0);
v_line_onX.setMagnitude(line_onX);
|
Примечание: мы используем классы из моих предыдущих уроков здесь. Vector2D был представлен в Gravity in Action , но вам не нужно читать его, чтобы использовать класс, он включен в исходную загрузку.
Второй фрагмент c1_circle здесь устанавливает B ( c1_circle ) и C ( c2_circle ) и проверяет наличие столкновения и наличие круга внутри сегмента или нет.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
|
private function refresh(e:Event):void {
for (var i:int = 0; i < circles.length; i++) {
//calculating line’s perpendicular distance to ball
var c1_circle:Vector2D = new Vector2D(circles[i].x — x1, circles[i].y — y1);
var c1_circle_onNormal:Number = c1_circle.projectionOn(leftNormal);
//Att2: get vector from c2 to circle
var c2_circle:Vector2D = new Vector2D(circles[i].x — x2, circles[i].y — y2);
circles[i].y += 2;
if (
c1_circle_onNormal <= circles[i].radius
&& v_line_onX.dotProduct(c1_circle) > 0
&& v_line_onX.dotProduct(c2_circle) < 0
){
//if collision happened, undo movement
circles[i].y -= 2;
}
}
}
|
Шаг 5: Результат
Вот результат для первого подхода. Нажмите на кнопку, чтобы сбросить позиции всех кругов в верхней части сцены.
Шаг 6: Второй подход
Второй подход намного проще. На этот раз я постараюсь вернуться назад с конца.
Соблюдайте схему ниже. Сегмент линии от c1 до c2. Понятно, что collide1 и collide3 находятся вне сегмента линии, и что только collide2 находится внутри сегмента линии.
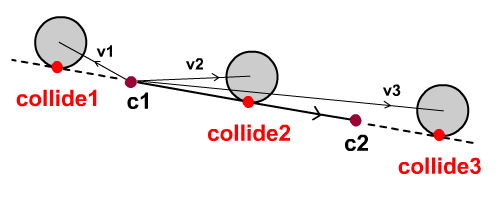
Пусть v1, v2 и v3 — векторы из c1 в соответствующие окружности. Только v2 и v3 параллельны — или, по крайней мере, указывают в аналогичных направлениях на линейный вектор (с1 по с2). Проверяя положительное значение в скалярном произведении между вектором линии и каждым из этих векторов от c1 до соответствующих центров окружности (v1, v2, v3), мы можем легко определить, что collide1 находится за отрезком линии. Другими словами, c1 . v1 . c1 . v1 .
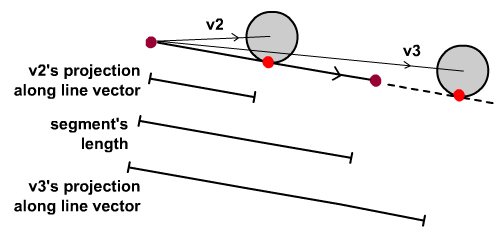
Далее мы разработаем метод, чтобы определить, что collide3 находится вне отрезка. Это должно быть легко. Очевидно, что проекция v3 вдоль вектора линии будет превышать длину отрезка. Мы будем использовать эту характеристику, чтобы отсеять столкновение3.
Итак, позвольте мне обобщить второй подход:
- Сначала мы проверяем пересечение между бесконечной прямой и окружностью.
- Если есть пересечение, дополнительно исследуйте следующее, чтобы определить, происходит ли это в отрезке линии:
- Убедитесь, что получено положительное значение, когда мы берем скалярное произведение вектора от c1 до круга и вектора линии, и
- Убедитесь, что величина проекции вектора на вектор линии меньше длины отрезка.
Шаг 7: Реализация
Вот реализация ActionScript выше:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
|
private function refresh(e:Event):void {
for (var i:int = 0; i < circles.length; i++) {
//calculating line’s perpendicular distance to ball
var c1_circle:Vector2D = new Vector2D(circles[i].x — x1, circles[i].y — y1);
var c1_circle_onNormal:Number = c1_circle.projectionOn(leftNormal);
//Att2: getting the relevant vectors
var c1_circle_onLine:Number = c1_circle.projectionOn(line);
circles[i].y += 2;
if (
Math.abs(c1_circle_onNormal) <= circles[i].radius
&& line.dotProduct(c1_circle) > 0
&& c1_circle_onLine < line.getMagnitude()
){
//if collision happened, undo movement
circles[i].y -= 2;
}
}
}
|
Шаг 8: Результат
По сути, он даст тот же результат, что и предыдущий, но, поскольку во втором подходе несколько строк кода короче, я думаю, это лучше.
Вывод
Надеюсь, это помогло. Спасибо за прочтение. Далее мы рассмотрим реакцию на столкновение.