В предыдущем уроке я продемонстрировал, как создать скользящую игру-головоломку с помощью HTML5 canvas.
Чтобы сэкономить время, я жестко закодировал начальные позиции плитки. Игровой процесс был бы лучше, если бы плитки были рандомизированы, но это привело бы к осложнениям, для объяснения которых потребовалось бы отдельное руководство.
Это тот урок.
Есть несколько способов рандомизировать плитки. Я рассмотрю несколько вариантов и расскажу об их сильных и слабых сторонах, а также о проблемах, которые возникают, и о том, как их преодолеть.
Один простой метод — инициализировать головоломку в разрешенном состоянии, а затем повторно вызывать функцию, чтобы вставить случайный кусок в пустое пространство.
function initTiles() { var slideLoc = new Object; var direction = 0; for (var i = 0; i < 30; ++i) { direction = Math.floor(Math.random()*4); slideLoc.x = emptyLoc.x; slideLoc.y = emptyLoc.y; if (direction == 0 && slideLoc.x > 0) { slideLoc.x = slideLoc.x - 1; } else if (direction == 1 && slideLoc.y > 0) { slideLoc.y = slideLoc.y - 1; } else if (direction == 2 && slideLoc.x < (tileCount - 1)) { slideLoc.x = slideLoc.x + 1; } else if (direction == 3 && slideLoc.y < (tileCount - 1)) { slideLoc.y = slideLoc.y + 1; } slideTile(emptyLoc, slideLoc); } } В этом случае мы сдвигаем 30 плиток, вдвое больше общего количества плиток в головоломке 4 × 4, и все же большинство фигур остаются на своих прежних местах. Чтобы получить что-то похожее на случайность, нам понадобится еще много итераций.
Это не эффективный способ рандомизировать головоломку. В идеале мы хотели бы переместить каждый кусок только один раз. Мы могли бы инициализировать головоломку до решенного состояния, а затем перебирать плитки, меняя каждую из них на произвольно выбранную плитку.
function initTiles() { for (var i = 0; i < tileCount; ++i) { for (var j = 0; j < tileCount; ++j) { var k = Math.floor(Math.random() * tileCount); var l = Math.floor(Math.random() * tileCount); swapTiles(i, j, k, l); } } } function swapTiles(i, j, k, l) { var temp = new Object(); temp = boardParts[i][j]; boardParts[i][j] = boardParts[k][l]; boardParts[k][l] = temp; }
Мало того, что этот метод дает нам гораздо более случайную конфигурацию, он делает это в меньшем количестве строк кода. Этот алгоритм, однако, имеет два серьезных недостатка. Первая проблема тонкая. Хотя обмен каждой плитки со случайным местоположением намного эффективнее, чем просто вставка фрагментов в пустой слот, этот алгоритм все еще не является действительно случайным. Некоторые стартовые позиции будут появляться гораздо чаще, чем другие.
В головоломке 2 × 2 некоторые начальные конфигурации будут встречаться на 87% чаще, чем другие. Добавьте третью строку, и некоторые конфигурации появятся в пять раз чаще, чем другие, и она будет ухудшаться по мере добавления новых плиток. К счастью, есть способ достичь истинной случайности, не добавляя дополнительной сложности. Он известен как алгоритм Фишера-Йейтса.
function initTiles() { var i = tileCount * tileCount - 1; while (i > 0) { var j = Math.floor(Math.random() * i); var xi = i % tileCount; var yi = Math.floor(i / tileCount); var xj = j % tileCount; var yj = Math.floor(j / tileCount); swapTiles(xi, yi, xj, yj); --i; } }
Математика Фишера-Йейтса выходит за рамки этого урока, но она дает каждой клетке равный шанс появиться в любом квадрате. Используя этот алгоритм, головоломка настолько случайна, насколько может получить функция Math.random() .
Но случайная замена тайлов — с помощью алгоритма Фишера-Йейтса или любого другого — приводит к другой проблеме. Половина всех возможных конфигураций плитки дает нам загадку, которую никогда не решить. Чтобы предотвратить раскрытие неразрешимой головоломки невинному пользователю, нам нужен еще один алгоритм.
Прежде чем я представлю этот алгоритм, мне нужно определить два термина: инверсия и полярность. Инверсия — это пара плиток, которые находятся в обратном порядке от того места, где они должны быть. Полярность головоломки заключается в том, является ли общее количество инверсий среди всех плиток четным или нечетным. Головоломка с 10 инверсиями имеет четную полярность; головоломка с 7 инверсиями имеет странную полярность.
Решенная загадка имеет нулевые инверсии (и даже полярность) по определению. Если бы мы поменяли местами две соседние плитки из решенной головоломки, у нас была бы одна инверсия.
В этой игре доска настроена как двумерный массив, каждый кусок которого представлен своими координатами x / y.
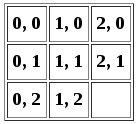
Но для работы с инверсиями и полярностью мы будем думать об этом как об одномерном массиве. Мы можем преобразовать координаты каждой плитки в одно число n по формуле n = y * w + x, где w — ширина. Изображенные в виде одномерного массива, плитки нумеруются следующим образом.
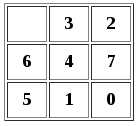
Теперь давайте рассмотрим случайную головоломку. Это может выглядеть так
Есть 19 инверсий. Плитка 6 перевернута со всеми шестью плитками, пронумерованными от 0 до 5; 3 инвертируется с 0, 1 и 2; 2 инвертируется с 0 и 1; 4 инвертируется с 0 и 1; 7 инвертируется с 0, 1 и 5; 5 инвертируется с 0 и 1; и 1 инвертируется с 0.
Чтобы получить эту сумму, нам нужна функция для подсчета инверсий для каждой плитки.
function countInversions(i, j) { var inversions = 0; var tileNum = j * tileCount + i; var lastTile = tileCount * tileCount; var tileValue = boardParts[i][j].y * tileCount + boardParts[i][j].x; for (var q = tileNum + 1; q < lastTile; ++q) { var k = q % tileCount; var l = Math.floor(q / tileCount); var compValue = boardParts[k][l].y * tileCount + boardParts[k][l].x; if (tileValue > compValue && tileValue != (lastTile - 1)) { ++inversions; } } return inversions; }
Теперь мы можем перебирать тайлы и сохранять текущую сумму инверсий.
function sumInversions() { var inversions = 0; for (var j = 0; j < tileCount; ++j) { for (var i = 0; i < tileCount; ++i) { inversions += countInversions(i, j); } } return inversions; }
Сдвиг плитки в сторону не меняет количество инверсий; пустой квадрат не имеет номера, поэтому замена его соседней плиткой всегда оставит нас с таким же количеством инверсий. Тем не менее, мы можем изменить количество инверсий при перемещении плитки вверх или вниз. Например, если мы сдвигаем плитку 6 вниз, мы уменьшаем количество инверсий с 19 до 17.
Правило состоит в том, что скольжение плитки вверх или вниз изменит ее отношение с плитками w — 1, где w — ширина головоломки. Таким образом, для головоломки 3 × 3 мы меняем отношение тайла с двумя другими тайлами. Это может привести к уменьшению двух инверсий, увеличению двух инверсий или отсутствию изменений. Например, в приведенной выше загадке, если сдвинуть плитку 5 вверх, мы получим 19 инверсий, поскольку получим инверсию с 4 и потеряем инверсию с 7.
Головоломка, которая начинается с четного числа инверсий, всегда будет иметь четное количество инверсий; головоломка с нечетным числом инверсий всегда будет иметь нечетное количество инверсий. Это верно не только для головоломки 3 × 3, но и для любой головоломки с нечетной шириной. Если мы когда-нибудь достигнем нуля инверсий, мы должны начать с четного числа.
Поскольку мы уже рассчитали количество инверсий, простая функция сообщит нам, разрешима ли головоломка.
function isSolvable() { return (sumInversions() % 2 == 0) }
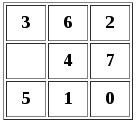
Приведенный выше пример не разрешим, так как 19 не является четным. Но предположим, что первые две плитки были перевернуты?
Теперь мы начнем с 18 инверсий. 3 и 6 больше не инвертированы, но все остальное остается прежним. У нас есть решаемая головоломка.
Это дает нам элегантное решение, которое сохраняет истинную случайность головоломки — каждая неразрешимая головоломка соединяется с уникальной разрешимой головоломкой, которая отличается только в первых двух тайлах.
if (!isSolvable()) { swapTiles(0, 0, 1, 0); initEmpty(); }
К сожалению, это не сработает, если одна из переставленных плиток — пустой квадрат. Нам понадобится специальный код для решения этой ситуации.
if (!isSolvable()) { if (emptyLoc.y == 0 && emptyLoc.x <= 1) { swapTiles(tileCount - 2, tileCount - 1, tileCount - 1, tileCount - 1); } else { swapTiles(0, 0, 1, 0); } initEmpty(); }
Если пустой квадрат находится в одном из первых двух мест, мы поменяем местами последние две плитки. Это немного искажает случайность, но мы все еще намного ближе, чем любой другой алгоритм может получить нас.
Осталась только одна проблема. Если ширина головоломки — четное число, сдвиг плитки вверх или вниз меняет полярность. Это потому, что, как мы видели выше, плитка меняет свои отношения с плитками w — 1.
Чтобы головоломка была разрешимой, она должна иметь равномерную полярность, когда пустой квадрат находится в нижнем ряду (при условии, что пустой квадрат находится в нижнем ряду, когда головоломка решена). Когда пустой квадрат находится в следующем ряду вверх, головоломка разрешима, если полярность нечетна. Таким образом, для головоломки четной ширины мы должны суммировать инверсии плюс расстояние между пустой строкой и нижней строкой.
function isSolvable(width, height, emptyRow) { if (width % 2 == 1) { return (sumInversions() % 2 == 0) } else { return ((sumInversions() + height - emptyRow) % 2 == 0) } }
Теперь мы должны отредактировать строку, которая вызывает эту функцию.
if (!isSolvable(tileCount, tileCount, emptyLoc.y + 1))
Здесь есть пара вещей, на которые стоит обратить внимание.
Во-первых, поскольку массив emptyLoc нуля, нам нужно добавить его перед сравнением с высотой.
Во-вторых, для квадратной головоломки технически нам не нужны два параметра для высоты и ширины; они имеют одинаковое значение, и мы tileCount переменную tileCount обоим. Но их разделение в функции проясняет, какое измерение используется в каждом уравнении. Если бы мы создали прямоугольную головоломку, мы бы знали, где использовать ширину и где использовать высоту.
Рандомизация скользящей головоломки, оказывается, в первую очередь больше, чем создание головоломки, но она стоит усилий, чтобы обеспечить лучшую игру. Вы можете увидеть пример случайной головоломки здесь .