Серия искусственного интеллекта. Часть 1. Поиск пути

Это руководство является первым из трех, в которых обсуждается, как использовать искусственный интеллект для создания игр и приложений, которые вы создаете. В этом первом уроке мы узнаем о поиске пути.

Окончательный результат предварительного просмотра

Давайте посмотрим на конечный результат, к которому мы будем стремиться:

Нажмите на точку, затем на другую точку, и ИИ определит кратчайший путь, чтобы добраться между ними. Вы можете использовать раскрывающийся список, чтобы выбрать алгоритм AI для использования.

Шаг 1: Обзор серии AI

Этот урок будет первым из трех, в которых будет рассказано, как использовать искусственный интеллект для создания игр и приложений, которые вы создаете. Вы можете подумать, что это звучит слишком сложно, но на самом деле все довольно просто! Я объясню два ключевых аспекта ИИ в играх, а затем создам классную игру, используя то, что мы изучаем. Надеюсь, вам понравится следить за этой короткой серией!

Шаг 2: Введение

В играх один из самых важных аспектов — сделать его очень эффективным, делать то, что должен, используя минимальные ресурсы. Для этого есть целая наука.

В этом уроке мы рассмотрим ключевой аспект в разработке игр: поиск пути. Мы обсудим 2 лучших метода, как они работают, как мы заставляем их работать в AS3, и, наконец, не в последнюю очередь, когда их использовать. Давайте начнем..

Шаг 3: Так что же такое Pathfinding?

Предположим, вы находитесь в середине леса с 50 различными потенциальными маршрутами перед вами, у вас почти нет энергии и вам нужно найти лучший выход, как бы вы это сделали?

Один вариант будет следовать за каждым из 50 маршрутов; метод проб и ошибок. Вы, конечно, выйдете, но это займет слишком много времени. Это не новая проблема, и многие люди придумали, как ее решить. Одним из них был Эдсгер В. Дейкстра, который разработал алгоритм для получения кратчайшего пути с учетом графика, источника и цели.

Прежде чем мы сможем приступить к решению проблемы, мы должны создать те элементы, граф, который содержит всю информацию, узлы, которые являются путевой точкой графа, и ребра, которые соединяют узлы. Думайте об этом как о графике, являющемся картой: узлы — это города, а края — соединяющие их магистрали.

Шаг 4: Настройка проекта

Прежде чем мы начнем кодировать, давайте сначала настроим наше рабочее пространство. Создайте новую папку и назовите ее «PathFinding». Внутри него создайте еще одну папку и назовите ее «График». Затем в папке PathFinding создайте новый FLA-файл Flash (AS3) и назовите его «PathFinding».

Шаг 5: Создание символа узла

В файле «PathFinding.fla» перейдите в меню «Вставка»> «Новый символ» и создайте новый мувиклип с именем «Узел». Выберите «экспорт для ActionScript» и в качестве класса напишите «Graph.Node»

Шаг 6: Рисуем узел

Внутри мувиклипа Node создайте новый круг с радиусом 25 и поместите его в центр. Затем добавьте новое текстовое поле, сделайте его динамическим, присвойте ему имя экземпляра «idx_txt» и поместите его в центр сцены.

Шаг 7: Создание узла

Каждый узел состоит из 2 основных элементов; индекс для его идентификации и его положение на графике. Имея это в виду, создайте новый класс внутри папки / пакета Graph и назовите его «Node». Сделайте так, чтобы он расширял класс sprite, затем просто добавьте две переменные: одну int для индекса и Vector3D для позиции. Также добавьте их соответствующий набор и методы get:

package Graph
{
    import flash.display.Sprite;
    import flash.geom.Vector3D;
 
    public class Node extends Sprite
    {
        private var pos:Vector3D;
        private var index:int;
        public function Node(idx:int,n_Pos:Vector3D)
        {
            index=idx;
            pos=n_Pos;
            this.x=n_Pos.x;
            this.y=n_Pos.y;
            idx_txt.text=String(idx)
        }
 
        public function getIndex():int
        {
            return index;
        }
        public function setPos(n_Pos:Vector3D):void
        {
            pos=n_Pos;
        }
 
        public function getPos():Vector3D
        {
            return pos;
        }
    }
}

Шаг 8: Создание края

Ребро содержит три элемента: индексы двух узлов, которые он соединяет, и его «стоимость» (или расстояние между узлами в этом случае). Снова в пакете / папке Graph создайте новый класс и назовите его «Edge»; заставить его снова расширить класс Sprite.

Теперь добавьте два целых числа для узлов и одно число для стоимости, затем добавьте соответствующий набор и методы get:

package Graph { import flash.display.Sprite;

Шаг 9: Создание графика

График является более сложным элементом, поскольку он должен хранить всю информацию. В папке Graph создайте новый класс и назовите его «Graph». Поскольку он просто содержит данные, нет необходимости расширять класс Sprite.

Граф будет содержать вектор со всеми узлами на графике, еще один вектор с ребрами, которые имеет каждый узел, и статический тип int, чтобы получить следующий индекс, доступный для узла. Таким образом, будет проще получить доступ ко всем элементам в графе, поскольку индекс узла является ключом вектора ребер, а это означает, что если вы хотите получить ребра узла с индексом 3, вы получите доступ к вектору ребер в положение 3, и вы получите края для этого узла.

Теперь давайте создадим эти переменные:

package Graph
{
    public class Graph
    {
        private static var nextIndex:int=0;
        private var nodes:Vector.<Node>;
        private var edges:Vector.<Array>;
 
        public function Graph()
        {
            nodes=new Vector.<Node>();
            edges=new Vector.<Array>();
        }
    }
}

Графу также нужны методы для добавления и получения узлов и ребер:

package Graph
{
    public class Graph
    {
        private static var nextIndex:int=0;
        private var nodes:Vector.<Node>;
        private var edges:Vector.<Array>;
 
        public function Graph()
        {
            nodes=new Vector.<Node>();
            edges=new Vector.<Array>();
        }
        //In order to get the node, we just ask for the index of it, and access the nodes vector with that key
        public function getNode(idx:int):Node
        {
            return nodes[idx];
        }
 
        //To get an edge, we ask for the two nodes that it connects,
        //then we retrieve all the edges of the from node and search if one of them
        //goes to the same node as the edge we are looking for, if it does, that’s our edge.
        public function getEdge(from:int,to:int):Edge
        {
            var from_Edges:Array = edges[from] as Array;
            for(var a:int=0;a<from_Edges.length;a++)
            {
                if(from_Edges[a].getTo()==to)
                {
                    return from_Edges[a];
                }
            }
            return null;
        }
 
        //To add a node to the graph, we first look if it already exist on it,
        //if it doesn’t, then we add it to the nodes vector, and add an array to the
        //edges vector where we will store the edges of that node, finally we increase
        //the next valid index int in order to give the next available index in the graph
        public function addNode(node:Node):int
        {
            if(validIndex(node.getIndex()))
            {
                nodes.push(node);
                edges.push(new Array());
                nextIndex++;
            }
            return 0;
        }
        //To add an edge we must first look if both nodes it connects actually exist,
        //then we must see if this edge already exist on the graph, finally we add it
        //to the array of edges of the node from where it comes
        public function addEdge(edge:Edge):void
        {
            if(validIndex(edge.getTo())&&validIndex(edge.getFrom()))
            {
                if(getEdge(edge.getFrom(),edge.getTo())==null)
                {
                    (edges[edge.getFrom()]as Array).push(edge);
                }
            }
        }
 
        //To get the edges of a node, just return the array given by the edges vector
        //at node’s index position
        public function getEdges(node:int):Array
        {
            return edges[node];
        }
 
        //This function checks if the node index is between the range of already added nodes
        //which is form 0 to the next valid index of the graph
        public function validIndex(idx:int):Boolean
        {
            return (idx>=0&&idx<=nextIndex)
        }
 
        //Just returns the amount of nodes already added to the graph
        public function numNodes():int
        {
            return nodes.length;
        }
 
        //This is to redraw all the edges on the graph to get them to the normal style
        public function redraw():void
        {
            for each(var a_edges:Array in edges)
            {
                for each(var edge:Edge in a_edges)
                {
                    edge.drawEdge(getNode(edge.getFrom()).getPos(),getNode(edge.getTo()).getPos());
                }
            }
        }
 
        //This function return the next valid node index to be added
        public static function getNextIndex():int
        {
            return nextIndex;
        }
    }
}

Шаг 10: Построение графика

Итак, теперь, когда у нас есть все необходимые элементы, давайте продолжим и построим график.

В папке PathFinding создайте новый класс и назовите его «Main», это будет наш основной класс:

package{
    import flash.display.Sprite;
 
    public class Main extends Sprite
    {
        public function Main()
        {
 
        }
    }
}

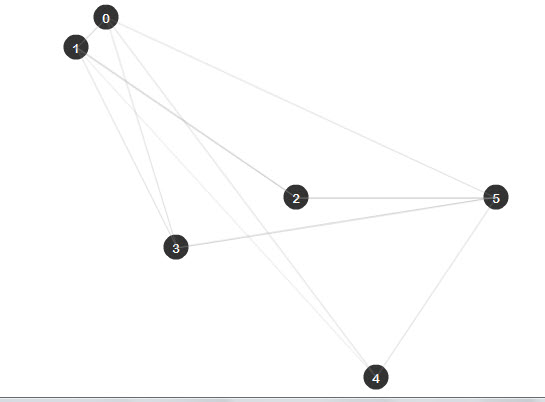
Теперь нам нужно импортировать только что созданные классы, так как они находятся в папке Graph. Затем создайте две переменные: одну для графа, а другую — массив позиций узлов, которые мы хотим добавить. После этого просто добавьте эти узлы и их ребра:

package{
    import flash.display.Sprite;
    import Graph.*;
    import flash.geom.Vector3D;
 
    public class Main extends Sprite
    {
        var graph:Graph = new Graph();
        //This array contains the position of the different nodes in the graph (x,y)
        var nodes:Array =new Array(
         [110,20],
         [80,50],
         [300,200],
         [180,250],
         [380,380],
         [500,200]
         );
         //This array contains the edges that connects the different nodes (from,to)
        var edges:Array = new Array(
        [0,1],[0,5],[0,3],
        [1,2],[1,0],[1,4],
        [2,1],[2,5],
        [3,1],[3,5],
        [4,0],[4,5],
        [5,2],[5,3]
        );
        public function Main()
        {
          //A loop in order to create all the nodes
            for(var a:int=0;a<nodes.length;a++)
            {
                var node:Node = new Node(Graph.Graph.getNextIndex(), new Vector3D(nodes[a][0],nodes[a][1]));
                graph.addNode(node);
                addChild(node);
            }
          //Another loop to create all the edges between nodes
            for(var b:int=0;b<edges.length;b++)
            {
                var from:int = edges[b][0];
                var to:int = edges[b][1];
 
                var edge:Edge = new Edge(from,to,Vector3D.distance(graph.getNode(from).getPos(),graph.getNode(to).getPos()));
                graph.addEdge(edge);
                //Since the drawEdge method requires the position vectors, we get the nodes
                //from the graph with their index and then get their position with getPos()
                edge.drawEdge(graph.getNode(from).getPos(),graph.getNode(to).getPos());
                addChild(edge);
            }
        }
    }
}

Шаг 11: Как выбрать правильный путь?

Как я уже говорил ранее, существует много способов получения пути между двумя узлами, например, DFS (глубокий первый поиск) или BFS (расширенный первый поиск), но иногда вы не просто хотите получить путь, соединяющий узлы. Вы также хотите получить «лучший» путь, который в большинстве случаев будет означать тот, который занимает меньше времени или самый близкий, в зависимости от того, что вы хотите.

В этом уроке я буду ссылаться на него как на тот, который стоит дешевле. (В нашем случае помните, что «стоимость» означает расстояние. В игре вы можете найти наименее опасный путь, или тот, который использует наименьшее количество топлива, или наименее видимый …)

Существуют алгоритмы, которые работают в зависимости от стоимости, наиболее важными из которых являются алгоритм Дейкстры и алгоритм A * (A-Star). Давайте сначала поговорим об алгоритме Дейкстры

Шаг 12: Введение в алгоритм Дейкстры

Этот алгоритм был создан Edsger Dijkstra в 1959 году. Он продвигается в зависимости от стоимости, которую представляет каждое ребро, всегда будут выбираться ребра с более низкой стоимостью, поэтому, когда вы достигнете цели, вы будете уверены, что путь — это путь с наименьшей стоимостью. доступный.

Шаг 13: Как работает алгоритм Дейкстры

Поскольку этот алгоритм работает с затратами, у нас должно быть место, где мы будем хранить стоимость перемещения на каждый узел из источника (начальный узел); назовите это вектором стоимости.

Например, если источником является узел 0, когда мы получим доступ к вектору стоимости в позиции 3, это будет возвращать самую низкую стоимость до сих пор при перемещении от 0 до 3. Нам также потребуется способ хранения кратчайшего пути: объясните дерево кратчайшего пути на следующем шаге.

Основные шаги алгоритма следующие:

Возьмите ближайший узел, еще не проанализированный.
Добавьте свой лучший край в дерево кратчайших путей.
Если это целевой узел, закончите поиск.
Получить все края этого узла.
Для каждого ребра рассчитывают стоимость перемещения от исходного узла к узлу прибытия.
Если общая стоимость этого ребра до сих пор меньше, чем стоимость узла прибытия, то обновите стоимость узла новым.
Возьмите следующий ближайший узел, еще не проанализированный.
Повторяйте это, пока цель не будет достигнута, или больше не будет доступных узлов.

Анимация будет иметь больше смысла. Здесь мы пытаемся получить от 1 до 6:

Шаг 14: Основные элементы алгоритма

Этот алгоритм состоит из разных векторов, в которых будет храниться вся необходимая информация, например, стоимость узлов или лучший путь до сих пор. Я объясню это лучше:

Вектор затрат: Здесь мы будем хранить лучшую стоимость до настоящего времени достижения определенного узла из источника. Например, если исходный узел равен 3 и мы обращаемся к элементу 6 вектора затрат, мы получим наилучшую найденную стоимость перемещения от 3, исходного узла, к узлу 6.
Дерево кратчайшего пути (SPT): этот вектор содержит край с наименьшей стоимостью, чтобы добраться до определенного узла. Это означает, что если мы получим доступ к элементу 7 SPT, он вернет наилучшее ребро для доступа к этому узлу.
Граница поиска (SF): этот вектор будет хранить наилучшее ребро, чтобы добраться до определенного узла, почти так же, как SPT, но в нем будут все узлы, которых еще нет в SPT. Это означает, что SF будет работать в качестве тестовой области, где мы будем тестировать все ребра для одного узла, когда все ребра будут проанализированы, мы будем уверены, что SF содержит лучший, поэтому мы можем добавить его в SPT.
Индексированная приоритетная очередь (pq): приоритетная очередь — это структура данных, которая всегда хранит свои элементы упорядоченным образом. Поскольку алгоритм должен сначала получить узел с наименьшей стоимостью, эта структура будет поддерживать узлы в порядке убывания в зависимости от их стоимости, но поскольку мы хотим получить индекс узла, а не саму стоимость, мы используем индексированную очередь с приоритетами , Например, если первый элемент pq — это узел 4, это будет означать, что он является самым дешевым.

Примечание: AS3 не содержит много структур данных, включая очередь с индексированными приоритетами , поэтому я написал ее для использования в этом руководстве. Чтобы получить его, просто скачайте исходные файлы и импортируйте папку utils папку PathFinding. Класс — это utils.IndexPriorityQ .

Шаг 15: Создайте папку алгоритма

Прежде чем мы начнем кодирование, в папке PathFinding создайте новую папку и назовите ее «Алгоритмы».

В этой новой папке создайте новый класс AS3 с именем «Dijkstra»:

package Algorithms {
 
    public class Dijkstra {
 
        public function Dijkstra() {
 
        }
 
    }
 
}

Шаг 16: Алгоритм Дейкстры в AS3

Теперь давайте закодируем алгоритм. Для этого потребуются три основные вещи: сам график, исходный узел и целевой узел; но мы также должны создать векторы, о которых мы только что говорили (Cost, SPT, SF). Не забудьте импортировать классы Graph:

package Algorithms {
 
    import Graph.Edge;
    import Graph.Graph;
    import utils.IndexedPriorityQ;
 
    public class Dijkstra {
 
        private var graph:Graph //The graph where the search will be made
        private var SPT:Vector.<Edge>;
        private var cost2Node:Vector.<Number>;
        private var SF:Vector.<Edge>;
        private var source:int;
        private var target:int;
 
        public function Dijkstra(g:Graph) {
 
        }
 
    }
 
}

Шаг 17: Функция поиска

После того, как мы настроили класс, мы можем начать кодирование алгоритма, который будет в функции «Поиск». Я объясню код с комментариями, поэтому, если у вас остались вопросы, вернитесь к шагам 12 и 13, чтобы напомнить себе, как работает этот алгоритм:

private function search():void
{
    //This will be the indexed priority Queue that will sort the nodes
    var pq:IndexedPriorityQ = new IndexedPriorityQ(cost2Node)
    //To start the algorithm we first add the source to the pq
    pq.insert(source);
    //With this we make sure that we will continue the search until there are no more nodes on the pq
    while(!pq.isEmpty())
    {
 
        /* 1.- Take the closest node not yet analyzed */
 
        //We get the Next Closest Node (NCN) which is the first element of the pq
        var NCN:int = pq.pop();
 
        /* 2.-Add its best edge to the Shortest Path Tree (Its best edge is stored on the SF) */
 
        SPT[NCN]=SF[NCN];
 
        //This will color the actual edge red in order to see which edges the algorithm has analyzed
        if(SPT[NCN])
        {
            SPT[NCN].drawEdge(
                graph.getNode(SPT[NCN].getFrom()).getPos(),
                graph.getNode(SPT[NCN].getTo()).getPos(),
                «visited»
            );
        }
 
        /* 3.- If it is the target node, finish the search */
 
        if(NCN==target)return;
 
        /* 4.- Retrieve all the edges of this node */
 
        var edges:Array=graph.getEdges(NCN);
 
        //With this loop we will analyze each of the edges of the array
        for each(var edge:Edge in edges)
        {
            /* 5.- For each edge calculate the cost of moving from the source node to the arrival Node */
 
            //The total cost is calculated by: Cost of the node + Cost of the edge
            var nCost:Number = cost2Node[NCN]+edge.getCost();
 
            //If the arrival node has no edge on the SF, then add its cost to the
            //Cost vector, the arrival node to the pq, and add the edge to the SF
            if(SF[edge.getTo()]==null)
            {
                cost2Node[edge.getTo()]=nCost;
                pq.insert(edge.getTo());
                SF[edge.getTo()]=edge;
            }
 
            /* 6.- If the cost of this edge is less than the cost of the arrival node until now, then update the node cost with the new one */
 
            else if((nCost<cost2Node[edge.getTo()])&&(SPT[edge.getTo()]==null))
            {
                cost2Node[edge.getTo()]= nCost;
                //Since the cost of the node has changed, we need to reorder again the pq to reflect the changes
                pq.reorderUp();
                //Because this edge is better, we update the SF with this edge
                SF[edge.getTo()]=edge;
            }
        }
    }
}

Шаг 18: Начало пути

Когда функция завершит поиск, у нас будет все путаница на SPT, так что мы можем его найти. Поскольку SPT имеет лучшее преимущество для доступа к узлу, мы можем работать в обратном направлении, чтобы получить лучший путь. Возьмите в качестве ссылки следующее изображение, полученное из предыдущей анимации:

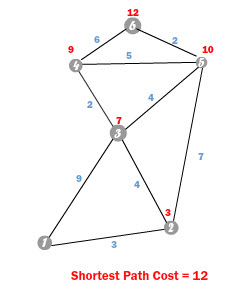
Если мы получим доступ к SPT на целевом узле, который в данном случае равен 6, он вернет наилучший фронт для достижения этого. Это было бы 6 — 5 края. Теперь, если мы повторим этот процесс с новым узлом, который идет с ребром, то 5 мы получим наилучшее ребро, чтобы добраться до этого узла, которое является ребром 5-2. Повторение этого процесса еще раз с узлом 2 даст нам ребро 2 — 1, так что мы, наконец, доберемся до начала, теперь, соединяя все эти ребра, мы получаем лучший путь: 6> 5> 2> 1.

Как вы видите, мы должны работать задом наперед, начиная с цели и переходя к источнику, чтобы получить лучший путь.

Шаг 19: функция getPath

Создайте новую функцию, которая будет возвращать массив с узлами пути, назовите его «getPath»:

public function getPath():Array
{
    var path:Array = new Array();
    if(target<0) return path;
    var nd:int = target;
    path.push(nd);
    while((nd!=source)&&(SPT[nd]!=null))
    {
        SPT[nd].drawEdge(
            graph.getNode(SPT[nd].getFrom()).getPos(),
            graph.getNode(SPT[nd].getTo()).getPos(),
            «path»
            );
        nd = SPT[nd].getFrom();
        path.push(nd);
    }
    path=path.reverse();
    return path;
}

Шаг 20: Полный урок Дейкстры

Мы закончили почти все, нам осталось заполнить конструктор и вызвать функцию поиска, поэтому класс будет выглядеть так:

package Algorithms{
 
    import Graph.Edge;
    import Graph.Graph;
    import utils.IndexedPriorityQ;
 
    public class Dijkstra {
 
        private var graph:Graph
        private var SPT:Vector.<Edge>
        private var cost2Node:Vector.<Number>
        private var SF:Vector.<Edge>
        private var source:int;
        private var target:int;
 
        public function Dijkstra(n_graph:Graph,src:int,tar=int) {
            graph=n_graph;
            source=src;
            target=tar;
            SPT= new Vector.<Edge>(graph.numNodes());
            cost2Node = new Vector.<Number>(graph.numNodes());
            SF = new Vector.<Edge>(graph.numNodes());
            search();
        }
        private function search():void
        {
            var pq:IndexedPriorityQ = new IndexedPriorityQ(cost2Node)
            pq.insert(source);
            while(!pq.isEmpty())
            {
 
                var NCN:int = pq.pop();
 
                SPT[NCN]=SF[NCN];
 
                if(SPT[NCN])
                {
                    SPT[NCN].drawEdge(
                        graph.getNode(SPT[NCN].getFrom()).getPos(),
                        graph.getNode(SPT[NCN].getTo()).getPos(),
                        «visited»
                    );
                }
 
                if(NCN==target)return;
 
                var edges:Array=graph.getEdges(NCN);
 
                for each(var edge:Edge in edges)
                {
                    var nCost:Number = cost2Node[NCN]+edge.getCost();
 
                    if(SF[edge.getTo()]==null)
                    {
                        cost2Node[edge.getTo()]=nCost;
                        pq.insert(edge.getTo());
                        SF[edge.getTo()]=edge;
                    }
 
                    else if((nCost<cost2Node[edge.getTo()])&&(SPT[edge.getTo()]==null))
                    {
                        cost2Node[edge.getTo()]= nCost;
                        pq.reorderUp();
                        SF[edge.getTo()]=edge;
                    }
                }
            }
        }
 
        public function getPath():Array
        {
            var path:Array = new Array();
            if((target<0)||(SPT[target]==null)) return path;
            var nd:int=target;
            path.push(nd);
            while((nd!=source)&&(SPT[nd]!=null))
            {
                SPT[nd].drawEdge(
                    graph.getNode(SPT[nd].getFrom()).getPos(),
                    graph.getNode(SPT[nd].getTo()).getPos(),
                    «path»
                );
                nd = SPT[nd].getFrom()
                path.push(nd);
            }
            path = path.reverse();
 
            return path;
        }
    }
}

Шаг 21: Создание нового графика

Чтобы увидеть лучший результат алгоритма, я написал класс, который помогает в создании графиков. Он называется Grapher и может быть найден в папке utils, которая поставляется с исходными файлами. Этот класс создает сетку узлов, откуда мы можем наблюдать, как алгоритм движется по графу.

С помощью этого класса снова откройте файл «Main.as» и измените его. Теперь у нас будет следующий код:

package{
    import flash.display.Sprite;
    import Graph.*;
    import utils.Grapher;
 
    public class Main extends Sprite
    {
        var graph:Graph = new Graph();
 
        public function Main()
        {
            //The parameters of the Grapher class are the width and height of the stage
            //the number of columns and rows, and then the graph for storing the data
            //After this we just add the grapher to the stage and we are done.
            //This will create a grid of nodes of 7*7
            var grapher:Grapher = new Grapher(550,400,7,7,graph);
            addChild(grapher);
        }
    }
}

Сохраните и запустите файл, и вы получите такой результат:

Шаг 22: Использование алгоритма Дейкстры

Теперь давайте продолжим поиск по новому алгоритму, который мы только что сделали. Импортируйте класс Dijkstra, создайте его экземпляр и вызовите функцию getPath:

package{
    import flash.display.Sprite;
    import Graph.*;
    import utils.Grapher;
    import Algorithms.Dijkstra;
 
    public class Main extends Sprite
    {
        var graph:Graph = new Graph();
 
        public function Main()
        {
            var grapher:Grapher = new Grapher(550,400,7,7,graph);
            addChild(grapher);
 
            //We create a new Dijkstra search that will look a path from node 24 to node 35
            var dijkstra:Dijkstra = new Dijkstra(graph,24,35);
            dijkstra.getPath();
        }
    }
}

Сохраните и запустите файл. Вы увидите края, которые алгоритм проанализировал, в виде красных линий, лучший найденный путь (от узла 24 до узла 35), представленный в виде черной линии:

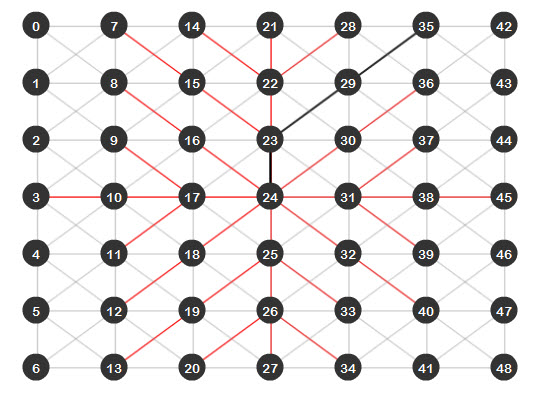
Шаг 23: разве нет ничего лучше?

Как мы видим, алгоритм Дейкстры находит кратчайший путь между двумя узлами, но, как показывает последнее изображение, много красных линий. Это означает, что все эти ребра были проанализированы, что не имеет большого значения, потому что у нас есть маленький граф, но представьте себе больший граф; это было бы слишком много граней для анализа. Если бы мы могли просто найти способ уменьшить это и сделать алгоритм еще более эффективным … я представляю вам алгоритм A * (A-Star).

Шаг 24: Алгоритм A *

Алгоритм A * является модифицированной версией Dijkstra. Он учитывает модифицированный способ получения стоимости каждого узла с помощью эвристического подхода. Это означает, что мы предоставляем небольшую «помощь» для алгоритма и сообщаем ему, куда идти, работая в качестве компаса и перемещая алгоритм непосредственно к цели.

Вместо того чтобы вычислять стоимость узла путем суммирования стоимости границы с сохраненной стоимостью узла, теперь она рассчитывается путем суммирования стоимости сохраненного узла и эвристической стоимости, которая является оценкой того, насколько близко к цели анализируется узел, который мы анализируем. , Эта новая стоимость называется стоимостью F

Шаг 25: Стоимость F

Стоимость F рассчитывается по следующей формуле: F = G + H, где G — стоимость узла, а H — эвристическая стоимость этого узла для цели. В этом уроке стоимость H будет рассчитываться с использованием евклидова расстояния между узлом и целью, которое представляет собой расстояние по прямой линии между двумя узлами.

Это означает, что в конце первыми проверяются узлы с более низкой стоимостью F, и поскольку стоимость F будет зависеть в основном от стоимости H, в конце алгоритм всегда будет определять приоритеты узлов, ближайших к цели.

Шаг 26: Алгоритм A * в AS3

В папке Algorithms создайте новый класс с именем «Astar». Переменные внутри класса будут почти такими же, как класс Dijkstra, но здесь у нас будет другой вектор для хранения стоимости F каждого узла:

package Algorithms{
    import Graph.Edge;
    import Graph.Graph;
    import flash.geom.Vector3D;
    import utils.IndexedPriorityQ;
 
    public class Astar {
        private var graph:Graph
        private var SPT:Vector.<Edge>
        private var G_Cost:Vector.<Number> //This vector will store the G cost of each node
        private var F_Cost:Vector.<Number> //This vector will store the F cost of each node
        private var SF:Vector.<Edge>
        private var source:int;
        private var target:int;
 
        public function Astar(n_graph:Graph,src:int,tar:int)
        {
            graph=n_graph;
            source=src;
            target=tar;
            SPT= new Vector.<Edge>(graph.numNodes());
            G_Cost = new Vector.<Number>(graph.numNodes());
            F_Cost = new Vector.<Number>(graph.numNodes());
            SF = new Vector.<Edge>(graph.numNodes());
            search();
        }
    }
}

Шаг 27: Новый класс поиска

Единственное различие между функцией поиска алгоритма Дейкстры и этой функцией заключается в том, что узлы будут отсортированы (в индексированной очереди приоритетов) в зависимости от вектора затрат F и что вектор затрат F будет определяться рассчитанной стоимостью H и сохраненным Стоимость G:

private function search():void
{
    //The pq is now sorted depending on the F cost vector
    var pq:IndexedPriorityQ = new IndexedPriorityQ(F_Cost)
    pq.insert(source);
    while(!pq.isEmpty())
    {
        var NCN:int = pq.pop();
        SPT[NCN]=SF[NCN];
        if(SPT[NCN])
        {
        SPT[NCN].drawEdge(
            graph.getNode(SPT[NCN].getFrom()).getPos(),
            graph.getNode(SPT[NCN].getTo()).getPos(),
            «visited»
        );
        }
        if(NCN==target)return;
        var edges:Array=graph.getEdges(NCN);
        for each(var edge:Edge in edges)
        {
            //The H cost is obtained by the distance between the target node, and the arrival node of the edge being analyzed
            var Hcost:Number = Vector3D.distance(
                graph.getNode(edge.getTo()).getPos(),
                graph.getNode(target).getPos())
            var Gcost:Number = G_Cost[NCN] + edge.getCost();
            var to:int=edge.getTo();
            if(SF[edge.getTo()]==null)
            {
                F_Cost[edge.getTo()]=Gcost+Hcost;
                G_Cost[edge.getTo()]=Gcost;
                pq.insert(edge.getTo());
                SF[edge.getTo()]=edge;
            }
            else if((Gcost<G_Cost[edge.getTo()])&&(SPT[edge.getTo()]==null))
            {
                F_Cost[edge.getTo()]=Gcost+Hcost;
                G_Cost[edge.getTo()]=Gcost;
                pq.reorderUp();
                SF[edge.getTo()]=edge;
            }
        }
    }
}

Шаг 28: Полный класс A *

Это единственные необходимые изменения, так как функция getPath одинакова для обоих классов. В конце класс будет таким:

package Algorithms {
    import Graph.Edge;
    import Graph.Graph;
    import flash.geom.Vector3D;
    import utils.IndexedPriorityQ;
 
    public class Astar {
        private var graph:Graph
        private var SPT:Vector.<Edge>
        private var G_Cost:Vector.<Number> //This vector will store the G cost of each node
        private var F_Cost:Vector.<Number> //This vector will store the F cost of each node
        private var SF:Vector.<Edge>
        private var source:int;
        private var target:int;
 
        public function Astar(n_graph:Graph,src:int,tar:int)
        {
            graph=n_graph;
            source=src;
            target=tar;
            SPT= new Vector.<Edge>(graph.numNodes());
            G_Cost = new Vector.<Number>(graph.numNodes());
            F_Cost = new Vector.<Number>(graph.numNodes());
            SF = new Vector.<Edge>(graph.numNodes());
            search();
        }
        private function search():void
        {
            //The pq is now sorted depending on the F cost vector
            var pq:IndexedPriorityQ = new IndexedPriorityQ(F_Cost)
            pq.insert(source);
            while(!pq.isEmpty())
            {
                var NCN:int = pq.pop();
                SPT[NCN]=SF[NCN];
                if(SPT[NCN])
                {
                SPT[NCN].drawEdge(
                    graph.getNode(SPT[NCN].getFrom()).getPos(),
                    graph.getNode(SPT[NCN].getTo()).getPos(),
                    «visited»
                );
                }
                if(NCN==target)return;
                var edges:Array=graph.getEdges(NCN);
                for each(var edge:Edge in edges)
                {
                    //The H cost is obtained by the distance between the target node, and the arrival node of the edge being analyzed
                    var Hcost:Number = Vector3D.distance(
                        graph.getNode(edge.getTo()).getPos(),
                        graph.getNode(target).getPos())
                    var Gcost:Number = G_Cost[NCN] + edge.getCost();
                    var to:int=edge.getTo();
                    if(SF[edge.getTo()]==null)
                    {
                        F_Cost[edge.getTo()]=Gcost+Hcost;
                        G_Cost[edge.getTo()]=Gcost;
                        pq.insert(edge.getTo());
                        SF[edge.getTo()]=edge;
                    }
                    else if((Gcost<G_Cost[edge.getTo()])&&(SPT[edge.getTo()]==null))
                    {
                        F_Cost[edge.getTo()]=Gcost+Hcost;
                        G_Cost[edge.getTo()]=Gcost;
                        pq.reorderUp();
                        SF[edge.getTo()]=edge;
                    }
                }
            }
        }
        public function getPath():Array
        {
            var path:Array = new Array();
            if(target<0) return path;
            var nd:int = target;
            path.push(nd);
            while((nd!=source)&&(SPT[nd]!=null))
            {
                SPT[nd].drawEdge(
                    graph.getNode(SPT[nd].getFrom()).getPos(),
                    graph.getNode(SPT[nd].getTo()).getPos(),
                    «path»
                    );
                nd = SPT[nd].getFrom();
                path.push(nd);
            }
            path=path.reverse();
            return path;
        }
    }
}

Шаг 29: Использование алгоритма A *

Еще раз откройте файл «Main.as» и импортируйте класс Astar, затем удалите созданный нами поиск Дейкстры, заменив его поиском A *:

package{
    import flash.display.Sprite;
    import Graph.*;
    import utils.Grapher;
    import Algorithms.Dijkstra;
    import Algorithms.Astar;
    public class Main extends Sprite
    {
        var graph:Graph = new Graph();
 
        public function Main()
        {
 
            var grapher:Grapher = new Grapher(550,400,7,7,graph);
            addChild(grapher);
 
            //We create a new Astar search that will look a path from node 24 to node 35
            var astar:Astar = new Astar(graph,24,35);
            astar.getPath();
        }
    }
}

Сохраните и запустите файл. Как видите, результат очень впечатляющий, нет красных линий, означающих, что поиск прошел непосредственно от источника к цели без анализа дополнительных ребер:

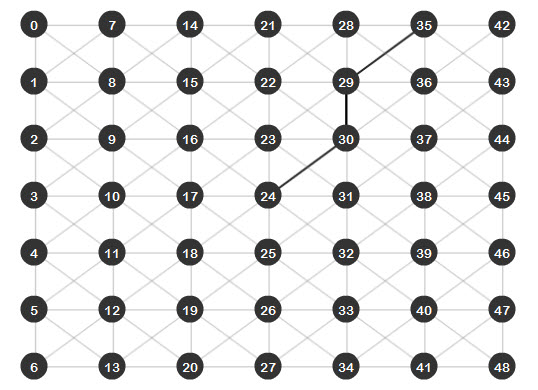
Шаг 30: Какой из них лучше?

Что ж, даже несмотря на то, что алгоритм A * быстрее и эффективнее обеспечивает прямой путь от источника к цели, в некоторых случаях Dijkstra будет лучшим вариантом.

Например, представьте себе игру в жанре RTS, где вы проинструктировали своего жителя пойти и найти некоторые ресурсы; с алгоритмом A * вам нужно будет выполнить поиск каждого ресурса на карте, а затем проанализировать, какой из них ближе. При поиске Dijkstra, поскольку он расширяет одинаковое количество по всем направлениям, первый найденный ресурс будет лучшим для сбора, и вы выполнили всего один поиск по сравнению со многими поисками A *.

По сути, вы захотите использовать алгоритм Дейкстры, когда вы выполняете общий поиск, и алгоритм A *, когда вы ищете конкретный элемент.

Вывод

Вот и все для этого урока, я надеюсь, вам понравилось и вы будете использовать его для своих проектов. Следите за следующим уроком этой серии AI и дайте мне знать, что вы об этом думаете.

Спасибо за прочтение! -Eduardo