В моем предыдущем уроке об обнаружении столкновений между кругом и линией я рассмотрел проекцию на линию, используя точечное произведение вектора. В этом уроке мы рассмотрим перпендикулярное скалярное произведение и используем его для прогнозирования точки пересечения для двух линий.
Окончательный результат предварительного просмотра
Давайте посмотрим на конечный результат, к которому мы будем стремиться. Используйте левую и правую клавиши со стрелками, чтобы направить корабль (треугольник), и нажмите вверх, чтобы временно увеличить скорость. Если спроектированная точка будущего столкновения находится на стене (линии), на ней будет нарисована красная точка. Для столкновения, которое «уже» произошло (то есть произошло бы в прошлом, исходя из текущего направления), красная точка все равно будет окрашена, но слегка прозрачна.
Вы также можете щелкнуть мышью и перетащить черные точки, чтобы переместить стену. Обратите внимание, что мы не только предсказываем место столкновения, но и время.
Шаг 1: Редакция
Прежде чем перейти к теме, давайте сделаем некоторые изменения. Вот уравнение скалярного произведения (ранее рассмотренное здесь ):

А вот определение перпендикулярного точечного произведения, извлеченное из Wolfram :
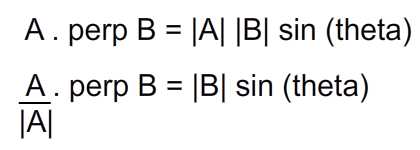
Шаг 2: Перпендикулярный точечный продукт
Теперь, чтобы помочь нам сформировать мысленную картину, я подготовил изображение ниже. Я уверен, что в этот момент вы можете получить вертикальные и горизонтальные компоненты вектора, поэтому компоненты, включающие синус и косинус, не должны быть проблемой.
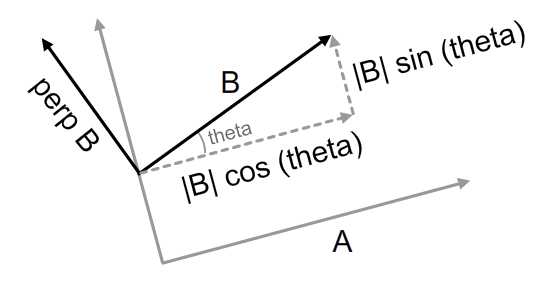
Давайте заменим оба компонента их эквивалентом. Я использовал A со шляпой для представления единичного вектора A (то есть вектора, который указывает в том же направлении, что и A, но имеет величину ровно 1). Еще одна деталь заключается в том, что перпендикуляр B фактически является правильной нормалью B — подробнее о нормалях на следующем шаге.
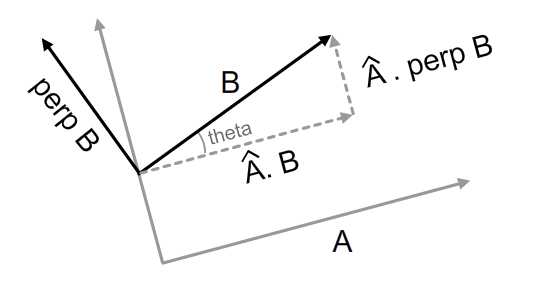
Из приведенной выше диаграммы видно, что проекция B на A даст |B|*cos (theta) . Но почему проекция нормального |B|*sin (theta) производит |B|*sin (theta) ?
Чтобы лучше понять это, я включил демонстрацию Flash ниже. Нажмите и перетащите черную стрелку. Когда вы осторожно двигаете его, вы заметите, что его перпендикулярная ось также следует за ним. Когда они поворачиваются, жирные красные линии также будут анимированными. Обратите внимание, что эти две длины одинаковы — отсюда и уравнение перпендикулярного точечного произведения.
Шаг 3: Нормалы
Нормы по определению лежат на перпендикулярной линии, пересекающей интересующую вас линию. Попробуем представить эти линии на геометрической плоскости.
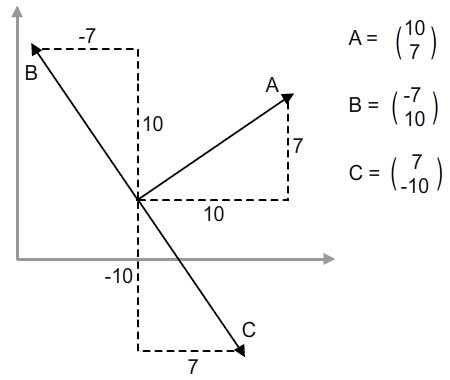
Декартова система координат используется на диаграмме выше. B — левая норма, а C — правая норма. Мы видим, что x-компонент B отрицателен (потому что он указывает налево), а y-компонент C отрицателен (потому что он направлен вниз).
Но обратите внимание на сходство между B и C. Их компоненты x и y такие же, как и у A, за исключением взбитых. Разница только в положении знака. Таким образом, мы приходим к выводу по изображению ниже.

Обратите внимание, что в этом примере мы имеем в виду именно декартову систему координат. Ось Y координатного пространства Flash — это отражение в декартовой системе, что приводит к перестановке между левой и правой нормалью.
Шаг 4: Проектирование точки столкновения
Чтобы выяснить точку столкновения вектора k на плоскости A, мы сначала свяжем хвост k с произвольной точкой на плоскости A. Для приведенного ниже случая вектор j является связующим вектором; тогда мы получим перпендикулярную проекцию k и j на плоскость A.
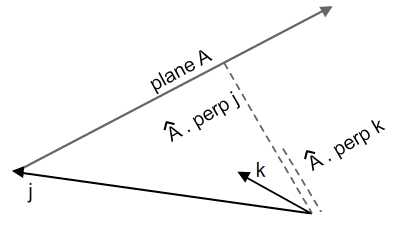
Красная точка на изображении ниже — это точка столкновения. И я надеюсь, что вы видите похожий треугольник на диаграмме ниже.
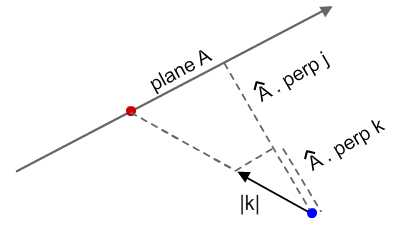
- | k |, величина вектора k
- Длина j на перпендикуляре плоскости A
- Длина k на перпендикуляре плоскости A
Таким образом, учитывая три вышеупомянутых компонента, мы можем использовать концепцию отношения для определения длины между красной и синей точками. Наконец, мы устанавливаем величину вектора k на указанную длину, и у нас есть точка столкновения!
Шаг 5: Реализация ActionScript
Итак, здесь идет реализация ActionScript. Я включил демо ниже. Попробуйте переместить стрелки так, чтобы обе линии пересекались. Маленькая черная точка будет отмечать точку пересечения линий. Обратите внимание, что эти сегменты не обязательно пересекаются, но бесконечные линии, которые они представляют, являются.
Вот скрипт, который делает расчеты. Проверьте Basic.as в исходной загрузке для полного сценария.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
private function recalculation ():void {
reorient();
/*Explain:
* v1 & v2 are vectors to represent both line segments
* v1 joins set1b(tail) to set1a (head) — analogous to vector k in diagram
* v2 joins set2b(tail) to set2a (head)
* toV2b is vector analogous to that of vector j in diagram
*/
var perp1:Number = v1.perpProduct(v2.normalise());
var toV2b:Vector2D = new Vector2D (set2b.x — set1b.x, set2b.y — set1b.y);
var perp2:Number = toV2b.perpProduct(v2.normalise());
/*Explain:
* length is calculated from the similar triangles ratio
* it is later used as magnitude for a vector
* that points in v1’s direction
*/
var length:Number = perp2 / perp1 * v1.getMagnitude();
var length_v1:Vector2D = v1.clone();
length_v1.setMagnitude(length);
/*Explain
* extend to locate the exact location of collision point
*/
intersec.x = set1b.x + length_v1.x;
intersec.y = set1b.y + length_v1.y;
}
|
Шаг 6: Линейные уравнения
Поэтому я надеюсь, что первый предложенный мной подход был легко понят. Я понимаю, что эффективность в получении точки пересечения важна, поэтому далее я предоставлю альтернативные подходы, хотя это потребует некоторых математических пересмотров. Потерпите меня!
Сначала поговорим о линейных уравнениях. Существует несколько форм уравнения линий, но в этом уроке мы коснемся двух из них:
- Общая форма
- Параметрическая форма
Я включил изображение ниже, чтобы помочь вам вспомнить. Те, кто заинтересован в этом, могут обратиться к этой записи в Википедии .

Шаг 7: Получение стандартной формы
Прежде чем выполнять какие-либо манипуляции с двумя линейными уравнениями, мы должны сначала вывести эти линейные уравнения. Рассмотрим сценарий, в котором нам даны координаты двух точек p1 (a, b) . и p2 (c, d) . Мы можем сформировать линейное уравнение, соединяющее эти две точки из градиентов:
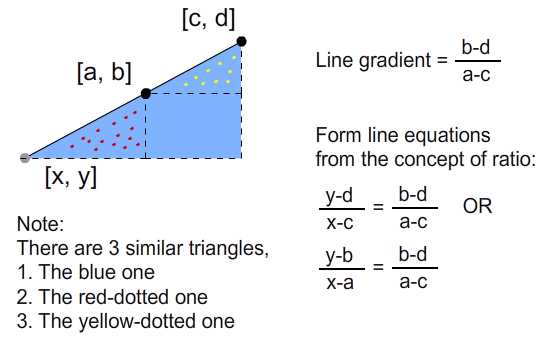
Затем, используя это уравнение, мы можем вывести константы A, B и C для стандартной формы:

Далее мы можем перейти к решению линейных уравнений одновременно.
Шаг 8: Решение одновременных уравнений
Теперь, когда мы можем сформировать линейные уравнения, давайте перейдем к двум линейным уравнениям и решим их одновременно. Учитывая эти два уравнения линии:
- Ex + Fy = G
- Px + Qy = R
Я приведу эти коэффициенты в таблицу в общем виде Ax + By = C.
| В | С | |
| Е | F | грамм |
| п | Q | р |
Чтобы получить значение y, мы делаем следующее:
- Умножьте обратные коэффициенты х для всего уравнения.
- Выполните операцию вычитания (сверху) для обоих уравнений.
- Переставить полученное уравнение через у.
| В | С | Умножить на | |
| Е | F | грамм | п |
| п | Q | р | Е |
И мы приходим к следующей таблице.
| В | С | |
| EP | FP | врач общей практики |
| PE | QE | RE |
После того как мы вычтем два уравнения, мы получим:
- y (FP — QE) = (GP — RE), который переставляет на:
- у = (GP — RE) / (FP — QE)
Переходим к получению х:
| В | С | Умножить на | |
| Е | F | грамм | Q |
| п | Q | р | F |
Мы приходим к следующей таблице
| В | С | |
| EQ | FQ | GQ |
| PF | QF | РФ |
После того, как мы вычтем два уравнения, мы получим:
- x (EQ — PF) = (GQ — RF), который переставляет на:
- х = (GQ — RF) / (EQ — PF)
Давайте дальше переставим у.
- у = (GP — RE) / (FP — QE)
- у = (GP — RE) / — (QE — FP)
- у = (RE — GP) / (QE — FP)
Таким образом, мы приходим к точке пересечения х и у. Мы замечаем, что они имеют один и тот же знаменатель.
- х = (GQ — RF) / (EQ — PF)
- у = (RE — GP) / (QE — FP)
Теперь, когда мы разработали математические операции и получили результат, просто добавьте значения, и у нас будет точка пересечения.
Шаг 9: Применение к ActionScript
Вот реализация Actionscript. Таким образом, все векторные операции сводятся к простой арифметике, но для этого сначала потребуются некоторые алгебраические работы.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
|
private function recalculation ():void {
reorient();
var E:Number = set1b.y — set1a.y;
var F:Number = set1a.x — set1b.x;
var G:Number = set1a.x * set1b.y — set1a.y * set1b.x;
var P:Number = set2b.y — set2a.y;
var Q:Number = set2a.x — set2b.x;
var R:Number = set2a.x * set2b.y — set2a.y * set2b.x;
var denominator:Number = (E * Q — P * F);
intersec.x = (G * Q — R * F) / denominator;
intersec.y = (R * E — G * P) / denominator;
}
|
Конечно, это тот же результат, что и в предыдущей демонстрации, только с меньшим количеством математики и без использования класса Vector2D .
Шаг 10: матричная альтернатива
Другой альтернативой решению этой проблемы является использование математической математики. Я снова приглашаю заинтересованных читателей погрузиться в лекцию профессора Вильдбергера об уравнениях линий . Здесь мы просто быстро рассмотрим концепцию.
По словам профессора Вильдбергера, есть две системы, которые мы можем использовать:
- Декартовы рамки
- Параметризованный векторный каркас
Давайте сначала пройдемся по декартовой. Проверьте изображение ниже.

Обратите внимание, что матрицы T и S содержат постоянные значения. То, что осталось неизвестным, это А. Таким образом, перестановка матричного уравнения в терминах А даст нам результат. Однако мы должны получить обратную матрицу T.
Шаг 11: Внедрение с AS3
Вот реализация вышеупомянутого с ActionScript:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
|
private function recalculation ():void {
reorient();
var E:Number = set1b.y — set1a.y;
var F:Number = set1a.x — set1b.x;
var G:Number = set1a.x * set1b.y — set1a.y * set1b.x;
var P:Number = set2b.y — set2a.y;
var Q:Number = set2a.x — set2b.x;
var R:Number = set2a.x * set2b.y — set2a.y * set2b.x;
var T:Matrix = new Matrix(E, P, F, Q);
T.invert();
var S:Matrix = new Matrix();
Sa = G;
S.concat(T);
intersec.x = Sa;
intersec.y = Sb;
}
|
Шаг 12: Параметрическая форма
Наконец, есть параметрическая форма уравнения линии, и мы попытаемся решить ее снова с помощью математической математики.
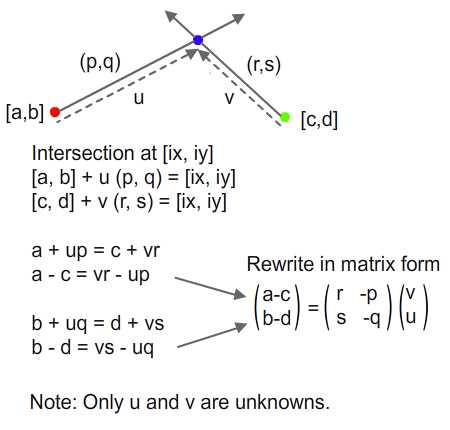
Мы хотели бы получить точку пересечения. Учитывая всю информацию, кроме u и v которую мы пытаемся найти, мы переписываем оба уравнения в матричную форму и решаем их.
Шаг 13: матричная манипуляция
Итак, еще раз, мы выполняем матричные манипуляции, чтобы прийти к нашему результату.

Шаг 14: Внедрение с AS3
Итак, вот реализация матричной формы:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
rivate function recalculation ():void {
reorient();
/*Explain:
* r, s are actually referring to components of v2 normalised
* p, q are actually referring to components of v1 normalised
*/
var norm_v2:Vector2D = v2.normalise();
var norm_v1:Vector2D = v1.normalise();
var a_c:Number = set1b.x — set2b.x;
var b_d:Number = set1b.y — set2b.y;
var R:Matrix = new Matrix;
Ra = norm_v2.x;
Rb = norm_v2.y;
R.invert();
var L:Matrix = new Matrix;
La = a_c;
Lb = b_d;
L.concat(R);
intersec.x = set2b.x + La * norm_v2.x;
intersec.y = set2b.y + La * norm_v2.y;
}
|
Шаг 15: Производительность
Мы рассмотрели четыре подхода к решению этой маленькой проблемы. Так что насчет производительности? Ну, я думаю, я просто оставлю этот вопрос на усмотрение читателей, хотя я считаю, что разница незначительна. Не стесняйтесь использовать этот жгут для тестирования производительности от Гранта Скиннера.
Итак, теперь, когда мы получили это понимание, что дальше? Примени это!
Шаг 16: Предсказание времени столкновения
Предположим, что частица движется по пути, который сталкивается со стеной. Мы можем рассчитать время воздействия с помощью простого уравнения:
Скорость = Смещение / Время
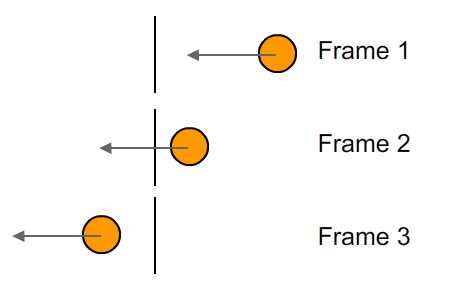
Представьте, что вы находитесь внутри этой оранжевой круглой частицы, и для каждого проходящего кадра делается объявление о времени столкновения со стеной. Вы услышите:
«Время удара: 1,5 кадра» — кадр 1
«Время удара: 0,5 кадра» — кадр 2
«Время удара: -0,5 кадра» — кадр 3
Когда мы достигаем кадра 3, столкновение с линией уже произошло (как указано отрицательным знаком). Вы должны перемотать время, чтобы достичь точки столкновения. Очевидно, что столкновение должно происходить некоторое время между кадрами 2 и 3, но Flash перемещается с шагом в один кадр. Таким образом, если столкновение произошло на полпути между кадрами, изменение знака на отрицательный укажет, что столкновение уже произошло.
Шаг 17: Отрицательное Время
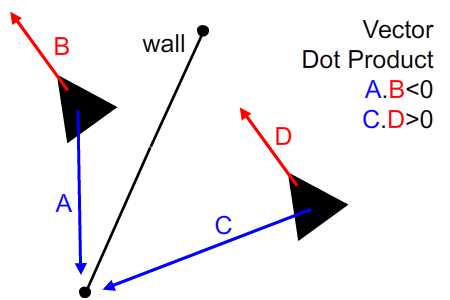
Чтобы получить отрицательное время, мы будем использовать произведение векторов. Мы знаем, что когда у нас есть два вектора и направление одного не находится в пределах 90 градусов по обе стороны от другого, они произведут произведение отрицательной точки. Кроме того, скалярное произведение является мерой того, насколько параллельны два вектора. Поэтому, когда столкновение уже произошло, скорость и направление вектора к точке на стене будут отрицательными — и наоборот.
Шаг 18: Реализация ActionScript
Итак, вот скрипт (включен в CollisionTime.as ). Я также добавил обнаружение столкновений в линейном сегменте здесь. Для тех, кто находит это незнакомым, обратитесь к моему руководству по обнаружению столкновений между кругом и отрезком , Шаг 6. А для помощи по управлению кораблями, вот еще одна ссылка .
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
//deciding if within wall segment
var w2_collision:Vector2D = new Vector2D(collision.x — w2.x, collision.y — w2.y);
collision.alpha = 0;
//when ship is heading to left of wall
if (w2_collision.dotProduct(v1) < 0) {
t.text = «Ship is heading to left of wall»;
}
else {
//when ship is heading to right of wall
if (w2_collision.getMagnitude() > v1.getMagnitude()) {
t.text = «Ship is heading to right of wall»
}
//when ship is heading to wall segment
else {
var ship_collision:Vector2D = new Vector2D(collision.x — ship.x, collision.y — ship.y);
var displacement:Number = ship_collision.getMagnitude();
if (ship_collision.dotProduct (velo) < 0) displacement *= -1;
//showing text
var time:Number = displacement / velo.getMagnitude();
t.text = «Frames to impact: » + time.toPrecision(3) + » frames.\n»;
time /= stage.frameRate;
t.appendText(«Time to impact: » + time.toPrecision(3) + » seconds.\n»);
//drop down alpha if collision had happened
if (displacement > 0) collision.alpha = 1;
else {
collision.alpha = 0.5;
t.appendText(«Collision had already happened.»)
}
}
}
|
Шаг 19: Окончательный результат
Итак, вот демонстрация того, что вы получите. Используйте левую и правую клавиши со стрелками, чтобы направить корабль (треугольник), и нажмите Вверх, чтобы временно увеличить скорость. Если предсказанная будущая точка столкновения находится на стене (линии), на ней будет нарисована красная точка. Для столкновения, которое уже «произошло», красная точка все равно будет окрашена, но слегка прозрачна. Вы также можете перетащить черные точки по обе стороны от стены, чтобы переместить ее.
Вывод
Поэтому я надеюсь, что этот урок был информативным. Делитесь, если вы действительно применили эту идею в другом месте от того, что я упомянул. Я планирую краткую статью о применении его для рисования лазерных целей — как вы думаете? Спасибо за чтение и дайте мне знать, если есть какие-либо ошибки.