Набор — это тип коллекции, который реализует основные алгоритмы алгебраического множества, включая объединение, пересечение, разность и симметричную разность. Каждый из этих алгоритмов будет подробно объяснен в соответствующих разделах.
обзор
Концептуально наборы — это наборы объектов, которые часто имеют некоторую общность. Например, у нас может быть набор, содержащий положительные четные целые числа:
[2, 4, 6, 8, 10, ...]
И набор, который содержит положительные нечетные целые числа:
[1, 3, 5, 7, 9, ...]
Эти два набора не имеют общих значений. Теперь рассмотрим третий набор, который является всеми факторами числа 100:
[1, 2, 4, 5, 10, 20, 25, 50, 100]
Учитывая эти наборы, мы теперь можем ответить на вопрос «Какие факторы 100 нечетны?», Посмотрев на набор нечетных целых чисел и набор факторов 100 и увидев, какие значения существуют в обоих наборах. Но мы также можем ответить на такие вопросы, как «Какие нечетные числа не являются коэффициентами 100?» Или «Какие положительные числа, четные или нечетные, не являются факторами 100?»
Это может показаться не очень полезным, но это потому, что пример несколько надуманный. Представьте, были ли наборы у каждого сотрудника компании и у каждого сотрудника, прошедшего обязательное ежегодное обучение.
Мы могли бы легко ответить на вопрос: «Какие сотрудники не прошли обязательное обучение?»
Мы можем продолжить добавлять дополнительные наборы и начать отвечать на очень сложные вопросы, такие как «Какие сотрудники, работающие полный рабочий день в отделе продаж, которым была выдана корпоративная кредитная карта, не прошли обязательное обучение по новому процессу отчетности о расходах?»
Установить класс
Класс Set реализует интерфейс IEnumerable и принимает универсальный аргумент, который должен иметь тип IComparable (проверка на равенство необходима для функционирования алгоритмов набора).
Члены набора будут содержаться в классе .NET List , но на практике наборы часто содержатся в древовидных структурах, таких как двоичное дерево поиска. Этот выбор базового контейнера влияет на сложность различных алгоритмов. Например, при использовании List , Contains имеет сложность O (n), тогда как при использовании дерева в среднем будет O (log n).
В дополнение к методам, которые мы будем реализовывать, Set включает конструктор по умолчанию и тот, который принимает IEnumerable элементов для заполнения набора.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
public class Set : IEnumerable
where T: IComparable
{
private readonly List _items = new List();
public Set()
{
}
public Set(IEnumerable items)
{
AddRange(items);
}
public void Add(T item);
public void AddRange(IEnumerable items);
public bool Remove(T item);
public bool Contains(T item);
public int Count
{
get;
}
public Set Union(Set other);
public Set Intersection(Set other);
public Set Difference(Set other);
public Set SymmetricDifference(Set other);
public IEnumerator GetEnumerator();
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator();
}
|
вставка
добавлять
| Поведение | Добавляет элемент в набор. Если элемент уже существует в наборе, генерируется исключение InvalidOperationException. |
| Производительность | На) |
При реализации алгоритма добавления необходимо принять решение: разрешит ли набор дублировать элементы или нет? Например, дан следующий набор:
[1, 2, 3, 4]
Если вызывающая сторона попытается добавить значение три, набор станет:
[1, 2, 3, 3, 4]
Хотя это может быть приемлемо в некоторых контекстах, это не то поведение, которое мы собираемся реализовать. Вообразите набор, который содержит всех студентов в местном колледже. Было бы нелогично разрешить добавление одного и того же ученика в набор дважды. Фактически, попытка сделать это, скорее всего, ошибка (и будет рассматриваться как таковая в этой реализации).
Примечание. При добавлении используется метод Contains
|
1
2
3
4
5
6
7
8
9
|
public void Add(T item)
{
if (Contains(item))
{
throw new InvalidOperationException(«Item already exists in Set»);
}
_items.Add(item);
}
|
AddRange
| Поведение | Добавляет несколько элементов в набор. Если в наборе существует какой-либо элемент входного перечислителя или если во входном перечислителе есть повторяющиеся элементы, будет выдано исключение InvalidOperationException. |
| Производительность | O (mn), где m — количество элементов во входном перечислении, а n — количество элементов в наборе. |
|
1
2
3
4
5
6
7
|
public void AddRange(IEnumerable items)
{
foreach (T item in items)
{
Add(item);
}
}
|
удалять
| Поведение | Удаляет указанное значение из набора, если оно найдено, и возвращает значение true. Если набор не содержит указанного значения, возвращается false. |
| Производительность | На) |
|
1
2
3
4
|
public bool Remove(T item)
{
return _items.Remove(item);
}
|
Содержит
| Поведение | Возвращает true, если набор содержит указанное значение. В противном случае возвращается false. |
| Производительность | На) |
|
1
2
3
4
|
public bool Contains(T item)
{
return _items.Contains(item);
}
|
подсчитывать
| Поведение | Возвращает количество элементов в наборе или 0, если набор пуст. |
| Производительность | O (1) |
|
1
2
3
4
5
6
7
|
public int Count
{
get
{
return _items.Count;
}
}
|
GetEnumerator
| Поведение | Возвращает перечислитель для всех элементов в наборе. |
| Производительность | O (1), чтобы вернуть перечислитель. Перечисление всех элементов имеет сложность O (n). |
|
1
2
3
4
5
6
7
8
9
|
public IEnumerator GetEnumerator()
{
return _items.GetEnumerator();
}
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator()
{
return _items.GetEnumerator();
}
|
Алгоритмы
союз
| Поведение | Возвращает новый набор, который является результатом операции объединения текущего и входного набора. |
| Производительность | O (mn), где m и n — количество элементов в предоставленном и текущем наборах соответственно. |
Объединение двух наборов — это набор, который содержит все отдельные элементы, которые существуют в обоих наборах.
Например, даны два набора (каждый представлен красным):
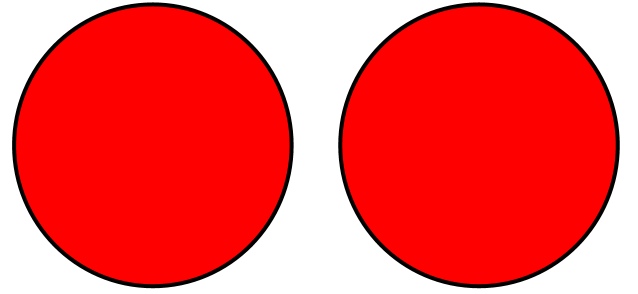
Когда выполняется операция объединения, выходной набор содержит все элементы в обоих наборах. Если в обоих наборах существуют какие-либо элементы, в выходной набор добавляется только одна копия каждого элемента.
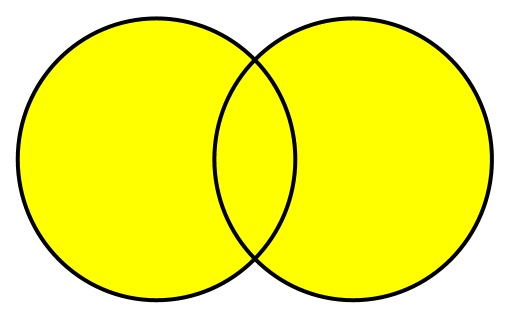
Более конкретный пример можно увидеть, когда мы объединяем несколько наборов целых чисел:
[1, 2, 3, 4] объединение [3, 4, 5, 6] = [1, 2, 3, 4, 5, 6]
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
|
public Set Union(Set other)
{
Set result = new Set(_items);
foreach (T item in other._items)
{
if (!Contains(item))
{
result.Add(item);
}
}
return result;
}
|
пересечение
| Поведение | Возвращает новый набор, который является результатом операции пересечения текущего и входного наборов. |
| Производительность | O (mn), где m и n — количество элементов в предоставленном и текущем наборах соответственно. |
Пересечение — это точка, в которой два набора «пересекаются», например, их общие элементы. Используя диаграмму Венна из примера объединения, здесь показано пересечение двух множеств:
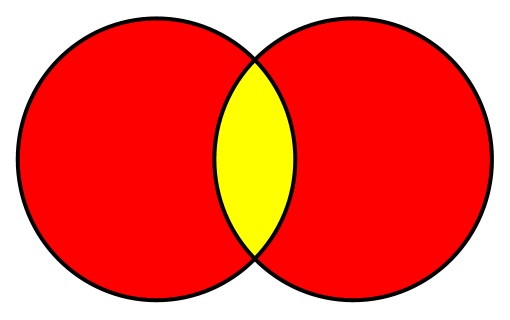
Или, используя наборы целых чисел:
[1, 2, 3, 4] пересекаются [3, 4, 5, 6] = [3, 4]
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
|
public Set Intersection(Set other)
{
Set result = new Set();
foreach (T item in _items)
{
if (other._items.Contains(item))
{
result.Add(item);
}
}
return result;
}
|
разница
| Поведение | Возвращает новый набор, который является результатом операции различий текущего и входного наборов. |
| Производительность | O (mn), где m и n — количество элементов в предоставленном и текущем наборах соответственно. |
Разница или разность наборов между двумя наборами — это элементы, которые существуют в первом наборе (наборе, для которого вызывается метод Difference ), но не существуют во втором наборе (параметр метода). Диаграмма Венна для этого метода показана здесь с возвращенным набором желтого цвета:
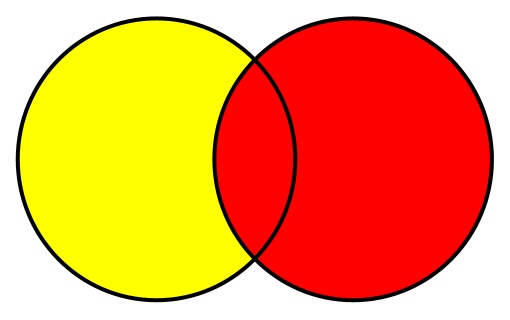
Или, используя наборы целых чисел:
[1, 2, 3, 4] разница [3, 4, 5, 6] = [1, 2]
|
01
02
03
04
05
06
07
08
09
10
11
|
public Set Difference(Set other)
{
Set result = new Set(_items);
foreach (T item in other._items)
{
result.Remove(item);
}
return result;
}
|
Симметричная разница
| Поведение | Возвращает новый набор, который является результатом операции симметричной разности текущего и входного наборов. |
| Производительность | O (mn), где m и n — количество элементов в предоставленном и текущем наборах соответственно. |
Симметричная разность двух наборов — это набор, членами которого являются те элементы, которые существуют только в одном или другом наборе. Диаграмма Венна для этого метода показана здесь с возвращенным набором в желтом
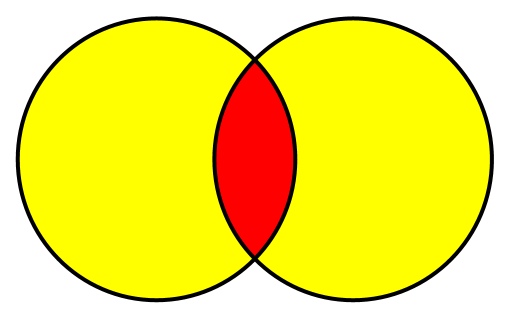
Или, используя целочисленные множества:
[1, 2, 3, 4] симметричная разность [3, 4, 5, 6] = [1, 2, 5, 6]
Возможно, вы заметили, что это полная противоположность операции пересечения. Имея это в виду, давайте посмотрим, что потребуется, чтобы найти симметричное различие, используя только те алгоритмы множеств, которые мы уже рассмотрели.
Давайте пройдемся по тому, что мы хотим.
Нам нужен набор, который содержит все элементы из обоих наборов, за исключением тех, которые существуют в обоих. Или, иначе говоря, мы хотим объединить оба множества, кроме пересечения обоих множеств. Мы хотим установить разницу между объединением и пересечением обоих множеств.
Шаг за шагом это выглядит так:
[1, 2, 3, 4] объединение [3, 4, 5, 6] = [1, 2, 3, 4, 5, 6]
[1, 2, 3, 4] пересечение [3, 4, 5, 6] = [3, 4]
[1, 2, 3, 4, 5, 6] установить разность [3, 4] = [1, 2, 5, 6]
Который дает результирующий набор, который мы хотели: ( [1, 2, 5, 6] ).
|
1
2
3
4
5
6
7
|
public Set SymmetricDifference(Set other)
{
Set union = Union(other);
Set intersection = Intersection(other);
return union.Difference(intersection);
}
|
IsSubset
Вы можете быть удивлены, почему я не добавил метод IsSubset . Этот тип метода обычно используется, чтобы определить, содержится ли один набор целиком в другом наборе. Например, мы могли бы знать, если:
[1, 2, 3] является подмножеством [0, 1, 2, 3, 4, 5] = true
В то время как:
[1, 2, 3] является подмножеством [0, 1, 2] = false
Причина, по которой я не детализировал метод IsSubset заключается в том, что он может быть выполнен с использованием существующих средств. Например:
[1, 2, 3] разница [0, 1, 2, 3, 4, 5] = []
Пустой набор результатов показывает, что весь первый набор содержался во втором наборе, поэтому мы знаем, что первый набор является полным подмножеством второго. Другой пример, используя пересечение:
[1, 2, 3] пересечение [0, 1, 2, 3, 4, 5] = [1, 2, 3]
Если выходной набор имеет то же количество элементов, что и входной набор, мы знаем, что входной набор является подмножеством второго набора.
В классе Set общего назначения наличие метода IsSubset может быть полезным (и может быть реализовано более оптимально); Тем не менее, я хотел подчеркнуть, что это не обязательно новое поведение, а скорее просто другой способ мышления о существующих операциях.
Следующий
Это завершает шестую часть о коллекции Set. Далее мы узнаем о последней теме этой серии, посвященной алгоритмам сортировки.