Мы видим линии, используемые во многих сценариях. Кривые также используются, хотя, возможно, не так часто — но это не подрывает их важность! В этом уроке мы более подробно рассмотрим кривые, в частности квадратичную и кубическую кривые, а также некоторые из их обычно используемых математических функций.
Окончательный результат предварительного просмотра
Давайте посмотрим на конечный результат, к которому мы будем стремиться. Перетащите красные точки и увидите изменение градиентов в положении.
А вот еще одна демонстрация с использованием кубических кривых без градиентов:
Шаг 1: Кривые
Квадратичные и кубические будут представлены в каждом из этих разделов. Итак, давайте сначала посмотрим на уравнение кривых. Эти уравнения записаны в полиномиальной форме, начиная с члена высшей степени. Первое — это квадратное уравнение (высшая степень 2); второе — кубическое уравнение (высшая степень 3).
\ [f (x) = Ax ^ 2 + Bx + C \ … (eq \ 1) \]
\ [g (x) = Ax ^ 3 + Bx ^ 2 + Cx + D \ … (eq \ 2) \]
Обратите внимание, что A, B, C и D являются действительными числами. Итак, теперь, когда мы знакомы с этим, давайте попробуем визуализировать это. Графические кривые будут нашей следующей попыткой.
Шаг 2: построение графиков кривых
Во-первых, давайте нарисуем квадратичную кривую. Я уверен, что все читатели изобразили квадратичную кривую на уроках математики в старшей школе, но просто чтобы освежить вашу память, я представляю графики ниже. Они размещены рядом, чтобы облегчить сравнение.
- Левый график использует декартово координатное пространство
- Правый график использует координатное пространство Flash
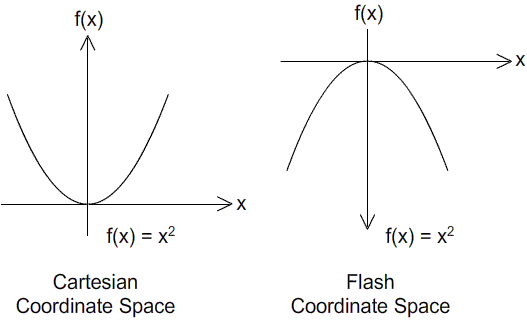
Очевидным отличием является инвертированная ось Y в координатном пространстве Flash. Они выглядят просто в целом, верно? Хорошо, теперь мы готовы построить график в пространстве координат Flash.
Шаг 3: Квадратичные коэффициенты
Чтобы расположить квадратные кривые в нужном месте, нам нужно понять их соответствующие уравнения. Нарисованная кривая действительно зависит от коэффициентов уравнения (для квадратичного случая это A, B и C).
Я включил презентацию Flash ниже, чтобы вы могли легко настроить эти коэффициенты и получить немедленную обратную связь.
Чтобы изучить влияние отдельных коэффициентов на общую кривую, я предлагаю выполнить следующие шаги, чтобы поэкспериментировать с представлением Flash выше.
- При установке A и B на 0 настройте значение C на положительные и отрицательные значения. Вы увидите изменение высоты линии.
- Теперь настройте значение B между положительными и отрицательными значениями. Посмотрите, что происходит с градиентом линии.
- Теперь настройте значение A между положительными и отрицательными значениями и сравните результаты.
- Затем настройте B между положительным и отрицательным снова. Обратите внимание, что кривая всегда прорезает начало координат.
- Наконец, настройте C. Наблюдайте весь сдвиг кривой вдоль оси Y.
Другое интересное наблюдение заключается в том, что на протяжении второго и третьего этапов, описанных выше, точка перегиба (т.е. точка поворота) остается в той же точке на оси y.
Шаг 4: Альтернативное уравнение 1
Вы быстро видите, что позиционирование кривой довольно сложно. Используемое уравнение нецелесообразно, если мы хотим, скажем, найти координаты самой низкой точки на кривой.
Решение? Мы перепишем уравнение в желаемую форму. Проверьте следующее уравнение:
\ [f (x) = P (x + Q) ^ 2 + R \]
Это все еще квадратное уравнение, но оно принимает другую форму. Теперь мы можем легко контролировать минимальные и максимальные точки на кривой. В предыдущей презентации Flash нажмите кнопку «Подход 1» в правом верхнем углу и поиграйте с новыми значениями.
Вот краткое объяснение ролей коэффициентов:
| Коэффициент | Роль |
| п | Управляйте крутизной кривой. |
| Q | Контролировать смещение точки поворота кривой вдоль оси x. |
| р | Контролировать смещение точки поворота кривой вдоль оси y. |
Тем не менее, это все еще трудная задача, чтобы заставить кривую проходить через данный набор точек. Нам пришлось бы тщательно рассчитать на бумаге, прежде чем переводить его в код.
К счастью, есть лучшее решение. Но прежде чем перейти к этому, давайте посмотрим на реализацию ActionScript на данный момент.
Шаг 5: Реализация ActionScript
Вот уравнения, написанные как функции ActionScript (см. Graphing.as в исходной загрузке ).
частная функция quadratic1 (x: номер, A: номер, B: номер, C: номер): номер { // y = A (x ^ 2) + B (x) + C вернуть A * x * x + B * x + C } частная функция quadratic2 (x: номер, P: номер, Q: номер, R: номер): номер { // y = P * (x + Q) ^ 2 + R вернуть P * (x + Q) * (x + Q) + R }
А вот реализация метода рисования с использованием Graphics.drawPath() . Просто обратите внимание, что все кривые в этой статье нарисованы одинаково.
Сначала переменные …
частные переменные точки: Vector. <Number> = новый Vector. <Number>; private var drawCommand: Vector. <int> = new Vector. <int>;
Теперь у-позиции рассчитываются на основе х-позиций и заданных коэффициентов.
перерисовка частной функции (A: номер, B: номер, C: номер): void { для (var i: int = 0; i <400; i ++) { var x: Number = i - 200; точки [i * 2] = x * 10 + stage.stageWidth >> 1; if (isApproach1) { очки [i * 2 + 1] = квадратичное1 (x, A, B, C) + stage.stageHeight >> 1 } еще { очки [i * 2 + 1] = квадратичное2 (x, A, B, C) + stage.stageHeight >> 1 } if (i == 0) drawCommand [i] = 1; иначе drawCommand [i] = 2; } graphics.clear (); graphics.lineStyle (1); graphics.drawPath (drawCommand, points); }
(Запутался в операторе >> ? Взгляните на этот урок .)
Шаг 6: Альтернативное уравнение два
Предположим, нам даны три точки, через которые должна пересечь квадратичная кривая; как мы формируем соответствующее уравнение? Более конкретно, как мы можем определить значения коэффициента уравнения? На помощь приходит линейная алгебра. Давайте проанализируем эту проблему.
Мы знаем, что квадратные уравнения всегда принимают форму, как написано в формуле. 1 на шаге 1.
\ [f (x) = Ax ^ 2 + Bx + C \ … (eq \ 1) \]
Поскольку все три приведенные координаты лежат на одной кривой, каждая из них должна удовлетворять этому уравнению с теми же коэффициентами, что и уравнение кривой, которую мы ищем. Давайте запишем это в форме уравнения.
Учитывая три coodinates:
- \ (S \ \ left (S_x, \ S_y \ right) \)
- \ (T \ \ left (T_x, \ T_y \ right) \)
- \ (U \ \ left (U_x, \ U_y \ right) \)
Подставьте эти значения в (уравнение 1). Обратите внимание, что A, B, C на данный момент неизвестны.
\ [f (x) = Ax ^ 2 + Bx + C \ … (eq \ 1) \]
- \ (S_y = A \ left (S_x \ right) ^ 2 + B \ left (S_x \ right) + C \ \)
- \ (T_y = A \ left (T_x \ right) ^ 2 + B \ left (T_x \ right) + C \ \)
- \ (U_y = A \ left (U_x \ right) ^ 2 + B \ left (U_x \ right) + C \ \)
Теперь перепишите в матричной форме. Обратите внимание, что A, B, C — неизвестные, для которых мы решаем.
[латекс]
\ begin {bmatrix} S_y \\ T_y \\ U_y \ end {bmatrix} =
\ Начать {bmatrix}
\ left (S_x \ right) ^ 2 & \ left (S_x \ right) & 1 \\
\ left (T_x \ right) ^ 2 & \ left (T_x \ right) & 1 \\
\ left (U_x \ right) ^ 2 & \ left (U_x \ right) & 1 \ end {bmatrix}
\ begin {bmatrix} A \\ B \\ C \ end {bmatrix} \\
[/латекс]
[латекс]
\ Начать {bmatrix}
\ left (S_x \ right) ^ 2 & \ left (S_x \ right) & 1 \\
\ left (T_x \ right) ^ 2 & \ left (T_x \ right) & 1 \\
\ left (U_x \ right) ^ 2 & \ left (U_x \ right) & 1 \ end {bmatrix} ^ {- 1}
\ begin {bmatrix} S_y \\ T_y \\ U_y \ end {bmatrix} =
\ Начать {bmatrix}
\ left (S_x \ right) ^ 2 & \ left (S_x \ right) & 1 \\
\ left (T_x \ right) ^ 2 & \ left (T_x \ right) & 1 \\
\ left (U_x \ right) ^ 2 & \ left (U_x \ right) & 1 \ end {bmatrix} ^ {- 1}
\ Начать {bmatrix}
\ left (S_x \ right) ^ 2 & \ left (S_x \ right) & 1 \\
\ left (T_x \ right) ^ 2 & \ left (T_x \ right) & 1 \\
\ left (U_x \ right) ^ 2 & \ left (U_x \ right) & 1 \ end {bmatrix}
\ begin {bmatrix} A \\ B \\ C \ end {bmatrix} \\
[/латекс]
[латекс]
\ Начать {bmatrix}
\ left (S_x \ right) ^ 2 & \ left (S_x \ right) & 1 \\
\ left (T_x \ right) ^ 2 & \ left (T_x \ right) & 1 \\
\ left (U_x \ right) ^ 2 & \ left (U_x \ right) & 1 \ end {bmatrix} ^ {- 1}
\ begin {bmatrix} S_y \\ T_y \\ U_y \ end {bmatrix}
= Я
\ begin {bmatrix} A \\ B \\ C \ end {bmatrix}
\\
K ^ {- 1} J = L
[/латекс]
Конечно, мы можем вместо этого использовать одновременные уравнения, но я предпочитаю использовать матрицы, потому что это проще. (Примечание редактора: если вы понимаете матрицы , то есть!)
Мы получим инверсию K и умножим на матрицу J, чтобы получить L. После того, как мы успешно решим для A, B, C, мы просто подставим в квадратное уравнение. Таким образом, у нас будет квадратичная кривая, которая проходит через все три точки.
Шаг 7: Импорт кораллов
Как уже упоминалось в предыдущем шаге, нам нужно выполнить инверсию матрицы 3×3 и умножение. Класс ActionScript flash.geom.matrix не сможет помочь в этом. Конечно, у нас есть выбор — использовать класс flash.geom.Matrix3D , но я предпочитаю библиотеку Coral, потому что я могу заглянуть в эти пользовательские классы и изучить, что происходит внутри. Лично я считаю это очень полезным, когда сомневаюсь в правильном использовании команд даже после прочтения документации по API.
Поэтому скачайте и поместите распакованные файлы Coral в исходную папку вашего проекта.
Шаг 8: Реализация ActionScript
Вот образец результата. Попробуйте изменить положение красных точек и увидеть, как квадратичная кривая перерисовывается, чтобы пересечь все три точки.
Шаг 9: Объяснение реализации
Вы можете найти полный скрипт в Draw_curve.as. Следующий код ActionScript предназначен только для включения элементов управления мышью на маленьких точках.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
public function Draw_Curve()
{
//setting up controls
c1 = new Circle(0xFF0000);
c2 = new Circle(0xFF0000);
c3 = new Circle(0xFF0000);
c1.addEventListener(MouseEvent.MOUSE_DOWN, move);
c1.addEventListener(MouseEvent.MOUSE_UP, move);
c2.addEventListener(MouseEvent.MOUSE_DOWN, move);
c2.addEventListener(MouseEvent.MOUSE_UP, move);
c3.addEventListener(MouseEvent.MOUSE_DOWN, move);
c3.addEventListener(MouseEvent.MOUSE_UP, move);
redraw()
}
private function move(e:MouseEvent):void {
if (e.type == «mouseDown») {
e.target.startDrag()
e.target.addEventListener(MouseEvent.MOUSE_MOVE, update);
}
else if (e.type == «mouseUp») {
e.target.stopDrag();
e.target.removeEventListener(MouseEvent.MOUSE_MOVE, update);
}
}
private function update(e:MouseEvent):void {
redraw();
}
|
Ядро лежит в функции redraw . Я выделил матричные операции и квадратичную функцию для процесса перерисовки.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
private function redraw():void
{
K = new Matrix3d( c1.x * c1.x, c1.x, 1, 0,
c2.x * c2.x, c2.x, 1, 0,
c3.x * c3.x, c3.x, 1, 0,
0, 0, 0, 1);
K.invert()
L = new Matrix3d( c1.y, 0, 0, 0,
c2.y, 0, 0, 0,
c3.y, 0, 0, 0,
0, 0, 0, 0);
L.append(K);
graphics.clear();
var points:Vector.<Number> = new Vector.<Number>;
var cmd:Vector.<int> = new Vector.<int>;
for (var i:int = 0; i < 200; i++) {
//current x
var x:Number = i * 2;
//f(x) = A (x^2) + B (x) + C
var y:Number = L.n11* x* x + L.n21 * x + L.n31 ;
points.push(x, y);
if (i == 0) cmd.push(1);
else cmd.push(2);
}
graphics.lineStyle(1);
graphics.drawPath(cmd, points);
}
|
Итак, вы можете видеть, что матрица K была инициализирована и инвертирована перед добавлением в матрицу J.
Функция append() умножает текущую матрицу J на расположенную слева от нее матрицу ввода K. Еще одна заслуживающая внимания деталь — мы не используем все строки и столбцы в матрицах K и J. Однако, поскольку инверсия матрицы может происходить только с квадратной матрицей, нам нужно заполнить 4-ую строку, 4-й элемент столбца K значением 1. (Нет необходимости делать это для J, потому что нам не нужна его инверсия в наших вычислениях. ) Таким образом, вы можете видеть, что все остальные элементы равны 0, кроме первого столбца.
Шаг 10: построение графика кубической кривой
Так что это все для рисования квадратичных кривых. Давайте перейдем к кубическим кривым.
Опять же, у нас будет небольшой пересмотр графика этих кривых. Проверьте следующее изображение:
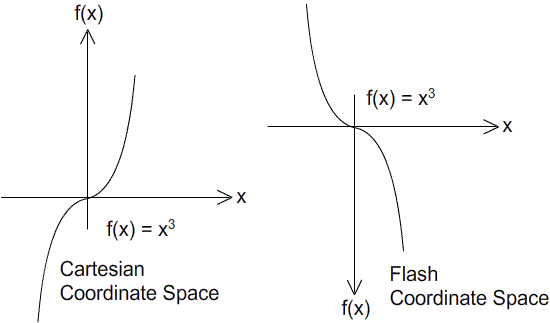
Когда вы сравните эту кривую с кривой квадратичного, вы заметите, что она круче, и что часть кривой находится ниже оси X. Одна половина отражается вертикально, по сравнению с квадратичной.
Шаг 11: Кубические коэффициенты
Я включил следующую презентацию Flash, чтобы вы могли поэкспериментировать с коэффициентами кубического уравнения. Попробуйте изменить значение A с положительного на отрицательное и наблюдать разницу в получаемой кривой.
Шаг 12: Реализация ActionScript
Вот важный раздел реализации приведенных выше графиков:
перерисовка частной функции (A: номер, B: номер, C: номер, D: номер): void { для (var i: int = 0; i <400; i ++) { var x: Number = i - 200; точки [i * 2] = x * 10 + stage.stageWidth >> 1; очки [i * 2 + 1] = куб. 1 (x, A, B, C, D) + stage.stageHeight >> 1 if (i == 0) drawCommand [i] = 1; иначе drawCommand [i] = 2; } graphics.clear (); graphics.lineStyle (1); graphics.drawPath (drawCommand, points); } частная функция cubic1 (x: номер, A: номер, B: номер, C: номер, D: номер): номер { // y = A (x ^ 3) + B (x ^ 2) + C (x) + D вернуть A * x * x * x + B * x * x + C * x + D }
Опять же, трудно расположить кубическую кривую в соответствии с набором точек, через которые она проходит. Еще раз, мы ссылаемся на линейную алгебру для альтернативы.
Шаг 13: Альтернативный метод
Из шага 6 мы знаем, что коэффициенты квадратного уравнения могут быть рассчитаны на основе трех заданных точек, и кривая, построенная из него, будет пересекать эти точки. Аналогичный подход может быть выполнен с любыми четырьмя заданными точками, чтобы получить кубическое уравнение:
- \ (S \ \ left (S_x, \ S_y \ right) \)
- \ (T \ \ left (T_x, \ T_y \ right) \)
- \ (U \ \ left (U_x, \ U_y \ right) \)
- \ (V \ \ left (V_x, \ V_y \ right) \)
Подставим эти координаты в (уравнение 2). Обратите внимание, что A, B, C, D неизвестны.
\ [g (x) = Ax ^ 3 + Bx ^ 2 + Cx + D \ … (eq \ 2) \]
- \ (S_y = A \ left (S_x \ right) ^ 3 + B \ left (S_x \ right) ^ 2 + C \ left (S_x \ right) + D \)
- \ (T_y = A \ left (T_x \ right) ^ 3 + B \ left (T_x \ right) ^ 2 + C \ left (T_x \ right) + D \)
- \ (U_y = A \ left (U_x \ right) ^ 3 + B \ left (U_x \ right) ^ 2 + C \ left (U_x \ right) + D \)
- \ (V_y = A \ left (V_x \ right) ^ 3 + B \ left (V_x \ right) ^ 2 + C \ left (V_x \ right) + D \)
Но теперь мы будем иметь дело с матрицей 4х4 вместо матрицы 3х3:
\ (
\ begin {bmatrix} S_y \\ T_y \\ U_y \\ V_y \ end {bmatrix} =
\ Начать {bmatrix}
\ left (S_x \ right) ^ 3 & \ left (S_x \ right) ^ 2 & \ left (S_x \ right) & 1 \\
\ left (T_x \ right) ^ 3 & \ left (T_x \ right) ^ 2 & \ left (T_x \ right) & 1 \\
\ left (U_x \ right) ^ 3 & \ left (U_x \ right) ^ 2 & \ left (U_x \ right) & 1 \\
\ left (V_x \ right) ^ 3 & \ left (V_x \ right) ^ 2 & \ left (V_x \ right) & 1 \ end {bmatrix}
\ begin {bmatrix} A \\ B \\ C \\ D \ end {bmatrix} \\
P = QR \\
Q ^ {- 1} P = Q ^ {- 1} QR \\
Q ^ {- 1} P = IR \\
Q ^ {- 1} P = R
\)
Теперь мы будем использовать все элементы в матрице 4×4 для Q и весь первый столбец для P. Затем Q инвертируется и применяется к P.
Шаг 14: Реализация ActionScript
Опять же, мы настроили элементы управления мышью, чтобы разрешить перетаскивание этих точек. При перетаскивании любой из этих точек постоянно происходит пересчет и перерисовка кривой.
публичная функция Draw_Curve2 () { // настройка элементов управления c1 = новый круг (0xFF0000); AddChild (с1); c1.x = stage.stageWidth * 0,2; c1.y = stage.stageHeight >> 1; c2 = новый круг (0xFF0000); AddChild (с2); c2.x = stage.stageWidth * 0,4; c2.y = stage.stageHeight >> 1; c3 = новый круг (0xFF0000); AddChild (с3); c3.x = stage.stageWidth * 0,6; c3.y = stage.stageHeight >> 1; c4 = новый круг (0xFF0000); AddChild (с4); c4.x = stage.stageWidth * 0,8; c4.y = stage.stageHeight >> 1; c1.addEventListener (MouseEvent.MOUSE_DOWN, move); c1.addEventListener (MouseEvent.MOUSE_UP, move); c2.addEventListener (MouseEvent.MOUSE_DOWN, move); c2.addEventListener (MouseEvent.MOUSE_UP, move); c3.addEventListener (MouseEvent.MOUSE_DOWN, переместить); c3.addEventListener (MouseEvent.MOUSE_UP, move); c4.addEventListener (MouseEvent.MOUSE_DOWN, переместить); c4.addEventListener (MouseEvent.MOUSE_UP, move); перерисовывать (); } перемещение частной функции (e: MouseEvent): void { if (e.type == "mouseDown") { e.target.startDrag () e.target.addEventListener (MouseEvent.MOUSE_MOVE, обновление); } else if (e.type == "mouseUp") { e.target.stopDrag (); e.target.removeEventListener (MouseEvent.MOUSE_MOVE, обновление); } } обновление приватной функции (e: MouseEvent): void { перерисовывать (); }
redraw является важнейшей функцией, где все произошло.
приватная функция redraw (): void { var left: Matrix3d = новая Matrix3d (c1.x * c1.x * c1.x, c1.x * c1.x, c1.x, 1, c2.x * c2.x * c2.x, c2.x * c2.x, c2.x, 1, c3.x * c3.x * c3.x, c3.x * c3.x, c3.x, 1, c4.x * c4.x * c4.x, c4.x * c4.x, c4.x, 1); left.invert () var right: Matrix3d = new Matrix3d (c1.y, 0, 0, 0, c2.y, 0, 0, 0, c3.y, 0, 0, 0, c4.y, 0, 0, 0); right.append (слева); // f (x) = A (x ^ 3) + B (x ^ 2) + C (x) + D graphics.clear (); var points: Vector. <Number> = новый вектор. <Number>; var cmd: Vector. <int> = new Vector. <int>; для (var i: int = 0; i <200; i ++) { var x: Number = i * 2; var y: Number = right.n11 * x * x * x + right.n21 * x * x + right.n31 * x + right.n41; points.push (x, y); if (i == 0) cmd.push (1); еще cmd.push (2); } graphics.lineStyle (1); graphics.drawPath (cmd, points); }
Наконец, давайте посмотрим на продукт. Нажмите и переместите красные точки, чтобы увидеть кубическую кривую, проходящую через все эти точки.
Шаг 15: полиномы высшей степени
Мы только что провели рисование полиномов степени 2 и 3 (квадратичный и кубический). Исходя из нашего опыта, мы можем предсказать, что для вычисления полинома степени 4 (квинтики) потребуется пять точек, для которых потребуется матрица 5×5, и так далее для полиномов еще более высоких степеней.
К сожалению, Coral и flash.geom.Matrix3D допускают только матрицы 4×4, поэтому вам придется написать свой собственный класс, если в этом возникнет необходимость. Хотя это редко требуется в играх.
Шаг 16: Разделение регионов
Попробуем применить наши знания для разделения регионов на нашей сцене. Это требует некоторого пересмотра неравенства уравнений. Проверьте изображение ниже.
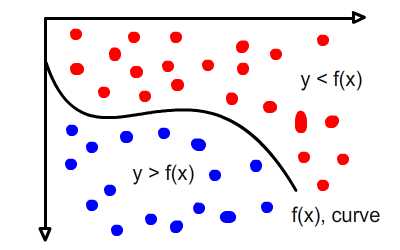
Это изображение выше показывает кривую, разделяющую области на две части:
- Синяя область сверху, где для каждой точки y больше, чем уравнение кривой.
- Красная область внизу, где для каждой точки у меньше уравнения кривой.
Нетрудно понять эту концепцию. Фактически, вы уже экспериментировали с этим в Шаге 11, когда настраивали коэффициенты кубической формулы. Представьте себе в системе координат, что существует бесконечное количество кривых, дифференцированных лишь небольшим изменением D:
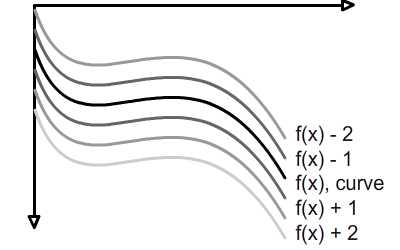
Шаг 17: Реализация ActionScript
Итак, вот пример выходных данных для квадратичной кривой. Вы можете попытаться переместить красную точку вокруг и увидеть окрашенные регионы.
Вот важный фрагмент ActionScript. Проверьте полный сценарий в Region_Curve.as
приватная функция redraw (): void { var left: Matrix3d = new Matrix3d (c1.x * c1.x, c1.x, 1, 0, c2.x * c2.x, c2.x, 1, 0, c3.x * c3.x, c3.x, 1, 0, 0, 0, 0, 1); left.invert () var right: Matrix3d = new Matrix3d (c1.y, 0, 0, 0, c2.y, 0, 0, 0, c3.y, 0, 0, 0, 0, 0, 0, 0); right.append (слева); // D = A (x ^ 2) + B (x) + C для каждого (var item: Circle in background) { var D: Number = right.n11 * item.x * item.x + right.n21 * item.x + right.n31; //trace(background[i].y); if (item.y> D) item.color = 0; иначе item.color = 0xAAAAAA; } }
Вот образец с учетом кубической кривой.
И реализация, которая идет с этим. Опять же, полный скрипт в Region_Curve2.as
// D = A + B (x) + C (x ^ 2) для каждого (var item: Circle in background) { var D: Number = right.n11 * item.x * item.x * item.x; + right.n21 * item.x * item.x + right.n31 * item.x + right.n41 //trace(background[i].y); if (item.y> D) item.color = 0; иначе item.color = 0xAAAAAA; }
Шаг 18: Вариации
Как насчет некоторых настроек, чтобы изменить цвет на разных кривых? Опять же, щелкните мышью на красных точках и увидите изменения градиента по всему экрану.
Шаг 19: Реализация ActionScript
Вот важный фрагмент ActionScript, извлеченный из Region_Curve3.as . Прежде всего мы хотим выяснить максимальное и минимальное смещение от исходной кривой.
var max: Number = 0; var min: Number = 0; var Ds: Vector. <Number> = новый вектор. <Number>; // D = A (x ^ 2) + B (x) + C для каждого (var item: Circle in background) { var D: Number = right.n11 * item.x * item.x + right.n21 * item.x + right.n31; смещение переменной: Number = item.y - D; Ds.push (смещение); if (item.y> D && offset> max) max = offset; иначе if (item.y <D && offset <min) min = offset; }
После этого мы применим его к окраске отдельных точек.
// изменения цвета в зависимости от смещения вар цвет: номер for (var i: int = 0; i <background.length; i ++) { if (Ds [i]> 0) { color = Ds [i] / max * 255 // вычисление цвета для слота в background [i] .color = color << 16 | цвет << 8 | цвет; // определить оттенки серого } иначе если (Ds [i] <0) { цвет = Ds [i] / мин * 255; background [i] .color = color << 16; // определяем градиент красного } }
Вывод
Так что все для рисования кривых. Далее находим корни квадратичной и кубической кривой. Спасибо за прочтение. Делитесь, если вы видите некоторые реальные приложения, которые используют преимущества этого учебника.