Статьи

Машинное обучение :: Извлечение текста (tf-idf) — Часть II

Октябрь 20, 2018

Первоначально Предоставленная Christain С. Perone

Читайте первую часть этого урока: извлечение текста функции (тс-IDF) — Часть I .

Этот пост является продолжением первой части, где мы начали изучать теорию и практику о выделении текстовых объектов и представлении модели векторного пространства. Я действительно рекомендую вам прочитать первую часть серии постов, чтобы следовать этому второму посту.

Так как первая часть этого урока понравилась многим, эта вторая часть немного длиннее первой.

Вступление

В первом посте мы узнали, как использовать термин-частота для представления текстовой информации в векторном пространстве. Тем не менее, основная проблема, связанная с частотно-частотным подходом, состоит в том, что он расширяет частые термины и уменьшает редкие термины, которые эмпирически более информативны, чем высокочастотные термины. Основная интуиция заключается в том, что термин, который часто встречается во многих документах, не является хорошим различителем и действительно имеет смысл (по крайней мере, во многих экспериментальных тестах); важный вопрос здесь: почему бы вам, например, в проблеме классификации выделить термин, который почти присутствует во всем корпусе ваших документов?

Вес tf-idf решает эту проблему. То, что дает tf-idf, это то, насколько важно слово для документа в коллекции, и поэтому tf-idf включает в себя локальные и глобальные параметры, потому что он учитывает не только изолированный термин, но и термин в пределах коллекции документов. Что делает tf-idf для решения этой проблемы, так это сокращает частые термины и увеличивает редкие; термин, встречающийся в 10 раз чаще, чем другой, не в 10 раз важнее, поэтому для этого tf-idf использует логарифмическую шкалу.

Но давайте вернемся к нашему определению, \ Mathrm {} тс (т, д)которое фактически является подсчетом термина Tв документе d. Использование этой простой частоты терминов может привести к таким проблемам, как спам по ключевым словам , то есть когда у нас есть повторяющийся термин в документе с целью повышения его ранжирования в системе IR ( информационного поиска ) или даже смещения в сторону длинных документов заставляя их выглядеть более важными, чем они есть, только из-за высокой частоты использования термина в документе.

Чтобы преодолеть эту проблему, термин частота \ Mathrm {} тс (т, д)документа в векторном пространстве обычно также нормализуется. Посмотрим, как мы нормализуем этот вектор.

Вектор нормализации

Предположим, мы собираемся нормализовать вектор частот-слагаемых, \ VEC {v_ {D_4}}который мы вычислили в первой части этого урока. Документ d4из первой части этого урока имел следующее текстовое представление:

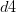
d4: We can see the shining sun, the bright sun.

И представление векторного пространства с использованием ненормализованной частоты-члена этого документа было:

\ vec {v_ {d_4}} = (0,2,1,0)

Для нормализации вектора, такое же , как вычисления единичного вектора вектора, и они обозначаются с помощью «хет» обозначения: \ Шляпа {v}. Определение единичного вектора \ Шляпа {v}вектора \ VEC {v}:

\ displaystyle \ hat {v} = \ frac {\ vec {v}} {\ | \ vec {v} \ | _p}

Где \ Шляпа {v}— единичный вектор или нормализованный вектор, \ VEC {v}— это вектор, который будет нормализован, и \ | \ VEC {v} \ | _pэто норма (величина, длина) вектора \ VEC {v}в L ^ рпространстве (не волнуйтесь, я собираюсь объяснить все это ).

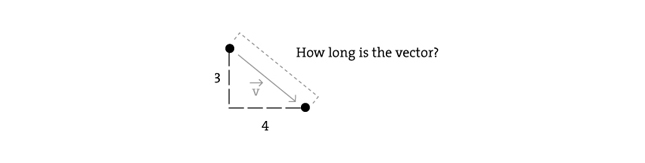
Единичный вектор на самом деле является не чем иным, как нормализованной версией вектора, это вектор, длина которого равна 1.

Источник: http://processing.org/learning/pvector/

Но важный вопрос здесь заключается в том, как рассчитывается длина вектора, и чтобы понять это, вы должны понять мотивацию L ^ рпространств, также называемых пространствами Лебега .

Пространства Лебега

Источник: http://processing.org/learning/pvector/

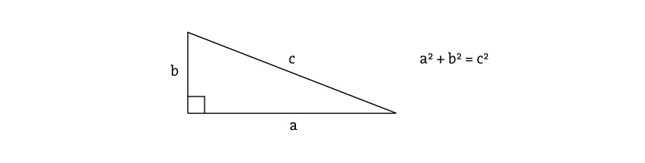
Обычно длина вектора 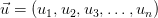\ vec {u} = (u_1, u_2, u_3, \ ldots, u_n)вычисляется с использованием евклидовой нормы — норма — это функция, которая присваивает строго положительную длину или размер всем векторам в векторном пространстве — что определяется следующим образом:

 Источник: http://processing.org/learning/pvector/

\ | \ VEC {и} \ | = \ sqrt {u ^ 2_1 + u ^ 2_2 + u ^ 2_3 + \ ldots + u ^ 2_n}

Но это не единственный способ определить длину, и поэтому вы видите (иногда) число пвместе с обозначением нормы, как в \ | \ VEC {и} \ | _p. Это потому, что это можно обобщить так:

\ displaystyle \ | \ vec {u} \ | _p = (\ left | u_1 \ right | ^ p + \ left | u_2 \ right | ^ p + \ left | u_3 \ right | ^ p + \ ldots + \ left | u_n \ right | ^ p) ^ \ frac {1} {p}

и упрощается как:

\ displaystyle \ | \ vec {u} \ | _p = (\ sum \ limit_ {i = 1} ^ {n} \ left | \ vec {u} _i \ right | ^ p) ^ \ frac {1} {p }

Поэтому, когда вы читаете о L2-норме , вы читаете о евклидовой норме , норме с р = 2, самой распространенной норме, используемой для измерения длины вектора, обычно называемой «величиной»; на самом деле, когда у вас есть неквалифицированная мера длины (без пчисла), у вас есть L2-норма (евклидова норма).

Когда вы читаете о норме L1 , вы читаете о норме с помощью р = 1:

\ displaystyle \ | \ vec {u} \ | _1 = (\ left | u_1 \ right | + \ left | u_2 \ right | + \ left | u_3 \ right | + \ ldots + \ left | u_n \ right |)

Что является не более чем простой суммой компонентов вектора, также известного как расстояние такси , также называемое расстоянием Манхэттена.

Геометрия такси по сравнению с евклидовым расстоянием: в геометрии такси все три изображенные линии имеют одинаковую длину (12) для одного и того же маршрута. В евклидовой геометрии зеленая линия имеет длину 6 \ раз \ sqrt {2} \ около 8,48и является уникальным кратчайшим путем.
Источник: Википедия :: Таксиаб Геометрия

Обратите внимание, что вы также можете использовать любую норму для нормализации вектора, но мы собираемся использовать наиболее распространенную норму, L2-Norm, которая также используется по умолчанию в выпуске 0.9 файла scikits.learn . Вы также можете найти документы, сравнивающие эффективность двух подходов среди других методов для нормализации вектора документа, фактически вы можете использовать любой другой метод, но вы должны быть краткими, как только вы используете норму, вы должны использовать ее для весь процесс напрямую связан с нормой ( единичный вектор, который использовал L1-норму, не будет иметь длины 1, если вы собираетесь взять его L2-норму позже ).

Вернуться к векторной нормализации

Теперь, когда вы знаете, что такое процесс нормализации вектора, мы можем попробовать конкретный пример — процесс использования L2-нормы (теперь мы будем использовать правильные термины), чтобы нормализовать наш вектор \ vec {v_ {d_4}} = (0,2,1,0), чтобы получить его единичный вектор \ Шляпа {v_ {D_4}}. Для этого мы просто подключим его к определению вектора модуля, чтобы оценить его:

\ hat {v} = \ frac {\ vec {v}} {\ | \ vec {v} \ | _p} \\ \\ \ hat {v_ {d_4}} = \ frac {\ vec {v_ {d_4} }} {|| \ vec {v_ {d_4}} || _2} \\ \\ \\ \ hat {v_ {d_4}} = \ frac {(0,2,1,0)} {\ sqrt {0 ^ 2 + 2 ^ 2 + 1 ^ 2 + 0 ^ 2}} \\ \\ \ hat {v_ {d_4}} = \ frac {(0,2,1,0)} {\ sqrt {5}} \ \ \\ \ small \ hat {v_ {d_4}} = (0,0, 0,89442719, 0,4472136, 0,0)

И это все! Наш нормализованный вектор \ Шляпа {v_ {D_4}}теперь имеет L2-норму \ | \ hat {v_ {d_4}} \ | _2 = 1.0.

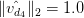
Обратите внимание, что здесь мы нормализовали наш вектор частоты документа термина, но позже мы собираемся сделать это после вычисления tf-idf.

Термин частота — обратная частота документа (tf-idf) вес

Теперь, когда вы поняли, как нормализация вектора работает в теории и на практике, давайте продолжим наше руководство. Предположим, у вас есть следующие документы в вашей коллекции (взяты из первой части урока):

Train Document Set:

d1: The sky is blue.
d2: The sun is bright.

Test Document Set:

d3: The sun in the sky is bright.
d4: We can see the shining sun, the bright sun.

Документ пространство может быть определено то , как , D = \ {d_1, d_2, \ ldots, d_n \}где Nэто количество документов в вашем корпусе, и в нашем случае , как D_ {train} = \ {d_1, d_2 \}и D_ {test} = \ {d_3, d_4 \}. Мощность нашего пространства документов определяется \ Влево | {D_ {поезд}} \ право | = 2и \ Влево | {D_ {испытание}} \ право | = 2, поскольку у нас есть только два документа для обучения и тестирования, но они, очевидно, не должны иметь одинаковую мощность.

Посмотрим теперь, как тогда определяется idf (частота обратных документов):

\ displaystyle \ mathrm {idf} (t) = \ log {\ frac {\ left | D \ right |} {1+ \ left | \ {d: t \ in d \} \ right |}}

где \ left | \ {d: t \ in d \} \ right |— количество документов, в которых Tпоявляется термин , когда функция «частота-термин» удовлетворяет \ mathrm {tf} (t, d) \ neq 0, мы только добавляем 1 в формулу, чтобы избежать деления на ноль.

Формула для tf-idf имеет вид:

\ mathrm {tf \ mbox {-} idf} (t) = \ mathrm {tf} (t, d) \ times \ mathrm {idf} (t)

и эта формула имеет важное следствие: высокий вес вычисления tf-idf достигается, когда у вас есть высокая частота термина (tf) в данном документе ( локальный параметр ) и низкая частота документа термина во всей коллекции ( глобальный параметр ).

Теперь давайте вычислим idf для каждого объекта, присутствующего в матрице объектов, с помощью частоты, которую мы вычислили в первом уроке:

M_ {train} = \ begin {bmatrix} 0 & 1 & 1 & 1 & 1 \\ 0 & 2 & 1 & 0 \ end {bmatrix}

Так как мы имеем 4 функции, мы должны вычислить \ Mathrm {IDF} (Т_1), \ Mathrm {IDF} (t_2), \ Mathrm {IDF} (t_3), \ Mathrm {IDF} (t_4):

\ mathrm {idf} (t_1) = \ log {\ frac {\ left | D \ right |} {1+ \ left | \ {d: t_1 \ in d \} \ right |}} = \ log {\ frac {2} {1}} = 0,69314718

 

\ mathrm {idf} (t_2) = \ log {\ frac {\ left | D \ right |} {1+ \ left | \ {d: t_2 \ in d \} \ right |}} = \ log {\ frac {2} {3}} = -0,40546511

 

\ mathrm {idf} (t_3) = \ log {\ frac {\ left | D \ right |} {1+ \ left | \ {d: t_3 \ in d \} \ right |}} = \ log {\ frac {2} {3}} = -0,40546511

 

\ mathrm {idf} (t_4) = \ log {\ frac {\ left | D \ right |} {1+ \ left | \ {d: t_4 \ in d \} \ right |}} = \ log {\ frac {2} {2}} = 0,0

Эти веса IDF могут быть представлены вектором как:

\ vec {idf_ {train}} = (0.69314718, -0.40546511, -0.40546511, 0.0)

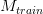
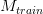
Now that we have our matrix with the term frequency (M_ {поезд}) and the vector representing the idf for each feature of our matrix (\ VEC {idf_ {поезд}}), we can calculate our tf-idf weights. What we have to do is a simple multiplication of each column of the matrix M_ {поезд} with the respective \ VEC {idf_ {поезд}} vector dimension. To do that, we can create a square diagonal matrix called M_ {IDF} with both the vertical and horizontal dimensions equal to the vector \ VEC {idf_ {поезд}} dimension:

M_ {idf} = \ begin {bmatrix} 0.69314718 & 0 & 0 & 0 \\ 0 & -0.40546511 & 0 & 0 \\ 0 & 0 & -0.40546511 & 0 \\ 0 & 0 & 0 & 0 \ end {bmatrix }

and then multiply it to the term frequency matrix, so the final result can be defined then as:

M_{tf\mbox{-}idf} = M_{train} \times M_{idf}

Please note that the matrix multiplication isn’t commutative, the result of A \times B will be different than the result of the B \times A, and this is why the M_{idf} is on the right side of the multiplication, to accomplish the desired effect of multiplying each idf value to its corresponding feature:

\begin{bmatrix} \mathrm{tf}(t_1, d_1) & \mathrm{tf}(t_2, d_1) & \mathrm{tf}(t_3, d_1) & \mathrm{tf}(t_4, d_1)\\ \mathrm{tf}(t_1, d_2) & \mathrm{tf}(t_2, d_2) & \mathrm{tf}(t_3, d_2) & \mathrm{tf}(t_4, d_2) \end{bmatrix} \times \begin{bmatrix} \mathrm{idf}(t_1) & 0 & 0 & 0\\ 0 & \mathrm{idf}(t_2) & 0 & 0\\ 0 & 0 & \mathrm{idf}(t_3) & 0\\ 0 & 0 & 0 & \mathrm{idf}(t_4) \end{bmatrix} \\ = \begin{bmatrix} \mathrm{tf}(t_1, d_1) \times \mathrm{idf}(t_1) & \mathrm{tf}(t_2, d_1) \times \mathrm{idf}(t_2) & \mathrm{tf}(t_3, d_1) \times \mathrm{idf}(t_3) & \mathrm{tf}(t_4, d_1) \times \mathrm{idf}(t_4)\\ \mathrm{tf}(t_1, d_2) \times \mathrm{idf}(t_1) & \mathrm{tf}(t_2, d_2) \times \mathrm{idf}(t_2) & \mathrm{tf}(t_3, d_2) \times \mathrm{idf}(t_3) & \mathrm{tf}(t_4, d_2) \times \mathrm{idf}(t_4) \end{bmatrix}

Let’s see now a concrete example of this multiplication:

M_{tf\mbox{-}idf} = M_{train} \times M_{idf} = \\ \begin{bmatrix} 0 & 1 & 1 & 1\\ 0 & 2 & 1 & 0 \end{bmatrix} \times \begin{bmatrix} 0.69314718 & 0 & 0 & 0\\ 0 & -0.40546511 & 0 & 0\\ 0 & 0 & -0.40546511 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix} \\ = \begin{bmatrix} 0 & -0.40546511 & -0.40546511 & 0\\ 0 & -0.81093022 & -0.40546511 & 0 \end{bmatrix}

And finally, we can apply our L2 normalization process to the M_{tf\mbox{-}idf} matrix. Please note that this normalization is “row-wise” because we’re going to handle each row of the matrix as a separated vector to be normalized, and not the matrix as a whole:

M_{tf\mbox{-}idf} = \frac{M_{tf\mbox{-}idf}}{\|M_{tf\mbox{-}idf}\|_2}
= \begin{bmatrix} 0 & -0.70710678 & -0.70710678 & 0\\ 0 & -0.89442719 & -0.4472136 & 0 \end{bmatrix}

And that is our pretty normalized tf-idf weight of our testing document set, which is actually a collection of unit vectors. If you take the L2-norm of each row of the matrix, you’ll see that they all have a L2-norm of 1.

Python practice

Environment Used: Python v.2.7.2, Numpy 1.6.1, Scipy v.0.9.0, Sklearn (Scikits.learn) v.0.9.

Now the section you were waiting for ! In this section I’ll use Python to show each step of the tf-idf calculation using the Scikit.learn feature extraction module.

The first step is to create our training and testing document set and computing the term frequency matrix:

from sklearn.feature_extraction.text import CountVectorizer

train_set = ("The sky is blue.", "The sun is bright.")
test_set = ("The sun in the sky is bright.",
"We can see the shining sun, the bright sun.")

count_vectorizer = CountVectorizer()
count_vectorizer.fit_transform(train_set)
print "Vocabulary:", count_vectorizer.vocabulary

# Vocabulary: {'blue': 0, 'sun': 1, 'bright': 2, 'sky': 3}

freq_term_matrix = count_vectorizer.transform(test_set)
print freq_term_matrix.todense()

#[[0 1 1 1]
#[0 2 1 0]]

Now that we have the frequency term matrix (called freq_term_matrix), we can instantiate the TfidfTransformer, which is going to be responsible to calculate the tf-idf weights for our term frequency matrix:

from sklearn.feature_extraction.text import TfidfTransformer

tfidf = TfidfTransformer(norm="l2")
tfidf.fit(freq_term_matrix)

print "IDF:", tfidf.idf_

# IDF: [ 0.69314718 -0.40546511 -0.40546511  0.        ]

Note that I’ve specified the norm as L2, this is optional (actually the default is L2-norm), but I’ve added the parameter to make it explicit to you that it it’s going to use the L2-norm. Also note that you can see the calculated idf weight by accessing the internal attribute called idf_. Now that fit() method has calculated the idf for the matrix, let’s transform the freq_term_matrix to the tf-idf weight matrix:

tf_idf_matrix = tfidf.transform(freq_term_matrix)
print tf_idf_matrix.todense()

# [[ 0.         -0.70710678 -0.70710678  0.        ]
# [ 0.         -0.89442719 -0.4472136   0.        ]]

And that is it, the tf_idf_matrix is actually our previous M_{tf\mbox{-}idf} matrix. You can accomplish the same effect by using the Vectorizer class of the Scikit.learn which is a vectorizer that automatically combines the CountVectorizer and the TfidfTransformer to you. See this example to know how to use it for the text classification process.

I really hope you liked the post, I tried to make it simple as possible even for people without the required mathematical background of linear algebra, etc. In the next Machine Learning post I’m expecting to show how you can use the tf-idf to calculate the cosine similarity.

If you liked it, feel free to comment and make suggestions, corrections, etc.

References

Understanding Inverse Document Frequency: on theoretical arguments for IDF

Wikipedia :: tf-idf

 The classic Vector Space Model

Sklearn text feature extraction code

Updates

Added the info about the environment used for Python examples

Source: http://pyevolve.sourceforge.net/wordpress/?p=1747

45
Share: