Краткое введение в модель векторного пространства (VSM)
В поиске информации или в интеллектуальном анализе текста термин частота — обратная частота документа, также называемый tf-idf , является хорошо известным методом оценки важности слова в документе. tf-idf также является очень интересным способом преобразования текстового представления информации в векторно-пространственную модель (VSM) или в разреженные функции, мы поговорим об этом позже, но сначала попробуем понять, что такое tf- IDF и VSM.
У VSM очень запутанное прошлое, см., Например, статью «Самая влиятельная статья, которую Джерард Сэлтон никогда не писал», в которой объясняется история цитируемой призраком статьи, которой на самом деле никогда не было; В общем, VSM — это алгебраическая модель, представляющая текстовую информацию в виде вектора, компоненты этого вектора могут представлять важность термина (tf – idf) или даже его отсутствие или присутствие ( Bag of Words ) в документе; важно отметить, что классический VSM, предложенный Salton, включает локальные и глобальные параметры / информацию (в том смысле, что он использует как анализируемый отдельный термин, так и весь сборник документов). VSM, интерпретируемый в lato sensu,пространство, в котором текст представлен как вектор чисел вместо его исходного текстового представления строки; VSM представляет функции, извлеченные из документа.
Давайте попробуем математически определить VSM и tf-idf вместе с конкретными примерами, для конкретных примеров я буду использовать Python (а также удивительный Python-модуль scikits.learn ).
Переход в векторное пространство
Первым шагом при моделировании документа в векторное пространство является создание словаря терминов, присутствующих в документах. Для этого вы можете просто выбрать все термины из документа и преобразовать его в измерение в векторном пространстве, но мы знаем, что есть какие-то слова (стоп-слова), которые присутствуют почти во всех документах, и что мы он извлекает из документов важные функции, функции идентифицируют их среди других похожих документов, поэтому использование таких терминов, как «есть, на, на» и т. д., не поможет нам, поэтому при извлечении информации мы просто проигнорирую их.
Давайте возьмем документы ниже, чтобы определить наше (глупое) пространство для документов:
Train Document Set: d1: The sky is blue. d2: The sun is bright. Test Document Set: d3: The sun in the sky is bright. d4: We can see the shining sun, the bright sun.
Теперь, что нам нужно сделать, это создать индексный словарь (словарь) слов из набора обучающих документов, используя документы 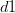

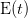

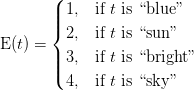
Обратите внимание, что такие термины, как «есть» и «the» были проигнорированы, как указано выше. Теперь, когда у нас есть индексный словарь, мы можем преобразовать набор тестового документа в векторное пространство, где каждый член вектора индексируется как наш индексный словарь, поэтому первый член вектора представляет «синий» термин нашего словаря, вторая представляет «солнце» и так далее. Теперь мы будем использовать термин-частота для представления каждого члена в нашем векторном пространстве; частота-термин является не чем иным, как мерой того, сколько раз термины, присутствующие в нашем словаре 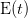
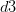
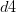

где 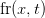
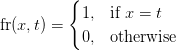
Итак, что 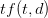


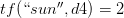
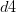
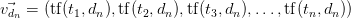
Каждое измерение вектора документа представлено термином словаря, например, 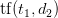

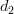
Давайте теперь покажем конкретный пример того, как документы 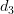
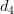
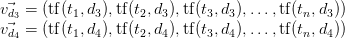
который оценивает:
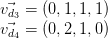
Как видно, документы так 
d3: The sun in the sky is bright. d4: We can see the shining sun, the bright sun.
The resulting vector 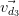
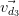
But wait, since we have a collection of documents, now represented by vectors, we can represent them as a matrix with 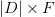
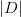
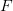

As you may have noted, these matrices representing the term frequencies tend to be very sparse (with majority of terms zeroed), and that’s why you’ll see a common representation of these matrix as sparse matrices.
Python practice
Environment Used: Python v.2.7.2, Numpy 1.6.1, Scipy v.0.9.0, Sklearn (Scikits.learn) v.0.9.
Since we know the theory behind the term frequency and the vector space conversion, let’s show how easy is to do that using the amazing scikit.learn Python module.
Scikit.learn comes with lots of examples as well real-life interesting datasets you can use and also some helper functions to download 18k newsgroups posts for instance.
Since we already defined our small train/test dataset before, let’s use them to define the dataset in a way that scikit.learn can use:
train_set = ("The sky is blue.", "The sun is bright.")
test_set = ("The sun in the sky is bright.",
"We can see the shining sun, the bright sun.")
In scikit.learn, what we have presented as the term-frequency, is called CountVectorizer, so we need to import it and create a news instance:
from sklearn.feature_extraction.text import CountVectorizer vectorizer = CountVectorizer()
The CountVectorizer already uses as default “analyzer” called WordNGramAnalyzer, which is responsible to convert the text to lowercase, accents removal, token extraction, filter stop words, etc… you can see more information by printing the class information:
print vectorizer CountVectorizer(analyzer__min_n=1, analyzer__stop_words=set(['all', 'six', 'less', 'being', 'indeed', 'over', 'move', 'anyway', 'four', 'not', 'own', 'through', 'yourselves', (...)
Let’s create now the vocabulary index:
vectorizer.fit_transform(train_set)
print vectorizer.vocabulary
{'blue': 0, 'sun': 1, 'bright': 2, 'sky': 3}
See that the vocabulary created is the same as 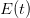
Let’s use the same vectorizer now to create the sparse matrix of our test_set documents:
smatrix = vectorizer.transform(test_set) print smatrix (0, 1) 1 (0, 2) 1 (0, 3) 1 (1, 1) 2 (1, 2) 1
Note that the sparse matrix created called smatrix is a Scipy sparse matrix with elements stored in a Coordinate format. But you can convert it into a dense format:
smatrix.todense() matrix([[0, 1, 1, 1], ........[0, 2, 1, 0]], dtype=int64)
Note that the sparse matrix created is the same matrix 
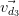

We’ll see in the next post how we define the idf (inverse document frequency) instead of the simple term-frequency, as well how logarithmic scale is used to adjust the measurement of term frequencies according to its importance, and how we can use it to classify documents using some of the well-know machine learning approaches.
I hope you liked this post, and if you really liked, leave a comment so I’ll able to know if there are enough people interested in these series of posts in Machine Learning topics.
References
The classic Vector Space Model
The most influential paper Gerard Salton never wrote