Оптимизация вызовов на хвосте

Если вы интересуетесь функциональным программированием, как и многие наши мастера, вы уже слышали разговоры о хвостовой рекурсии. Хвостовая рекурсия относится к рекурсивному вызову функции, который был сделан из хвостовой позиции . Когда вызов функции находится в конечном положении, это означает, что больше нет инструкций между возвратом управления из вызываемой функции и оператором возврата вызывающей функции. Мы проиллюстрируем это некоторыми примерами кода, но сначала, почему это важно?

В 1977 году Гай Л. Стил представил документ в АСМ, в котором он суммировал дебаты о GOTO и структурированном программировании, и он заметил, что вызовы процедур в хвостовой позиции процедуры могут лучше всего рассматриваться как прямая передача контроля вызываемому процедура. Это, утверждал он, устранит ненужные операции манипуляции со стеком, которые привели людей к искусственному восприятию того, что GOTO более эффективен, чем вызовы процедур.

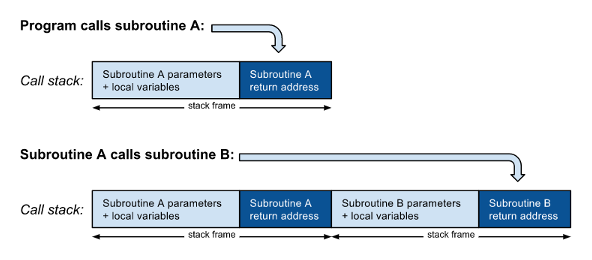
На самом базовом уровне функция или процедура — это подпрограмма, вызываемая инструкцией перехода к точке входа в подпрограмму. Отличие подпрограммы от простого перехода заключается в том, что вызывающий код должен сначала вставить адрес возврата (адрес следующей инструкции, которая будет выполнена после возврата подпрограммы) в стек вызовов, прежде чем перейти к подпрограмме. Параметры подпрограммы и локальные переменные также хранятся в стеке, который может быть стеком вызовов или отдельным:

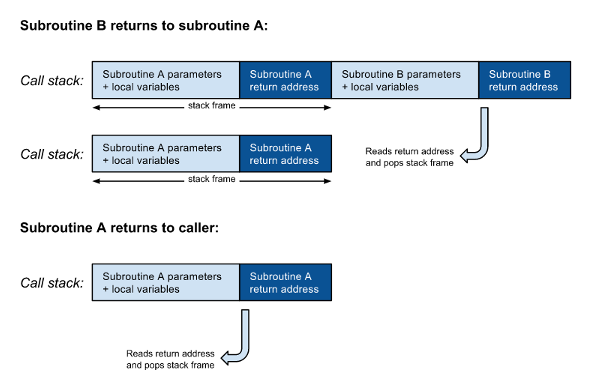
Как показано на рисунке 1 , когда подпрограмма A вызывает другую подпрограмму B , новый кадр стека, включающий адрес возврата, должен быть помещен в стек вызовов поверх адреса возврата из A. Когда B завершает работу, он читает адрес возврата, извлекает свой кадр стека из стека вызовов и возвращается к вызывающей стороне A. Когда подпрограмма A завершает свою работу, она выполняет аналогичные действия:

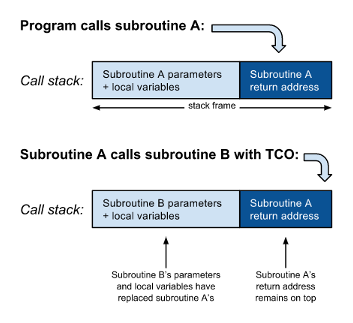
Однако, когда вызов подпрограммы B находится в хвостовой позиции, больше нет инструкций между возвратом управления из B и оператором возврата A. Другими словами, программа вернется из B только для немедленного возврата к вызывающей стороне A. Следовательно, нет необходимости помещать адрес возврата из B в стек вызовов: программа может просто перейти к B и, когда она завершится, она будет считывать адрес возврата A из стека вызовов и возвращаться непосредственно к вызывающему объекту A. Более того, больше не будет использоваться локальные переменные или параметры A , поэтому они могут быть заменены параметрами и локальными переменными для B :

Таким образом, вызов подпрограммы в хвостовой позиции можно эффективно оптимизировать, заменив его инструкцией перехода. По этой причине оптимизация хвостового вызова также называется устранением хвостового вызова. Это важно, потому что каждый раз, когда рекурсивная подпрограмма вызывает себя без TCO, она требует больше места для стека. Рекурсивная программа всегда сталкивается с опасностью нехватки места, с которой не сталкивается эквивалентная нерекурсивная программа. Это особенно важно для программ, написанных в функциональном стиле.

Когда мы программируем в императивном стиле, рекурсия — это инструмент, который мы можем использовать в тех случаях, когда это соответствует характеру проблемы; мы помним о требованиях к памяти и предпринимаем шаги, чтобы избежать перегрузки стека. Проблема предполагает новое измерение в функциональном программировании, потому что рекурсия является методом выбора для реализации итерации. Императивная программа может вполне успешно повторить цикл десять миллионов раз. Было бы совершенно неприемлемо, чтобы функциональная программа не могла выполнять те же вычисления. Оптимизация Tail Call позволяет нам писать рекурсивные программы, которые не увеличивают стек таким образом. Когда Гай Стил разработал Scheme с Джеральдом Джеем Суссманом, они определили требование в определении языка, что TCO должен быть реализован компилятором. К сожалению, это не относится ко всем функциональным языкам.

Рассмотрим этот надуманный пример хвостовой рекурсивной программы на Java:

sumReduce , что рекурсивный вызов sumReduce находится в хвостовой позиции, поскольку после его оценки во внешнем вызове больше ничего не нужно делать, кроме как возвращать значение. При настройках памяти JVM по умолчанию эта процедура выдает ошибку переполнения стека при вызове со списком из десяти тысяч целых чисел.

Чтобы проиллюстрировать, как некоторые функциональные языки решают эту проблему, давайте перепишем функцию sumReduce в Clojure:

Написание Clojure, как это в реальной жизни, не рекомендуется; то же самое может быть лучше выполнено с помощью (reduce + integers) но мы будем игнорировать это для обсуждения. Функция sum-reduce представляет точно такую ​​же проблему, что и ее Java-аналог:

Чтобы обойти эту проблему, Clojure предоставляет форму (loop (recur)) :

Теперь функция вполне способна суммировать десять миллионов целых чисел и более (хотя reduce все еще быстрее):

Но это не оптимизация хвостового вызова. Документация Clojure описывает loop-recur как «хак, так что что-то вроде хвостовой рекурсивной оптимизации работает в clojure». Это говорит о том, что оптимизация хвостового вызова недоступна в JVM, в противном случае повторение цикла не потребуется. К сожалению, это действительно так.

Возвращаясь к обсуждению, с которого мы начали, важное различие с TCO состоит в том, что go to является более общим, чем конструкция цикла; это также может оптимизировать взаимную рекурсию. Это невозможно путем преобразования хвостовой рекурсии в цикл. Чтобы проиллюстрировать это на нетривиальном примере, рассмотрим решение Clojure популярной игры в боулинг ката:

Эта программа является взаимно рекурсивной: sum-up-score вызывает score-strike , score-spare score-no-mark и score-no-mark , и каждый из этих трех повторяет вызов суммирующему баллу. Прямые ссылки на итоговый счет делают необходимым объявить его в начале. Все вызовы находятся в хвостовой позиции и, следовательно, будут кандидатами на TCO — если бы JVM могла это сделать — но невозможно использовать loop-recur.

В этом видео архитектор языка и библиотек Java Брайан Гетц объясняет историческую причину, по которой JVM не поддерживала хвостовую рекурсию: некоторые чувствительные к безопасности методы зависели от подсчета кадров стека между кодом библиотеки JDK и кодом вызова, чтобы выяснить, кто их вызывал , ТШО вмешался бы в это. Он добавляет, что этот код теперь заменен, и что поддержка хвостовой рекурсии находится в отставании, хотя и не с очень высоким приоритетом. С ростом интереса к функциональному программированию и, в частности, к росту функциональных языков, работающих на JVM, таких как Clojure и Scala, количество случаев поддержки TCO в JVM растет.