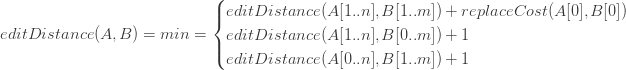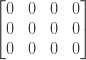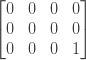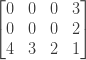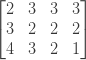Следуя теме предыдущего поста , я расскажу о другой проблеме, которая может быть эффективно решена с помощью динамического программирования. В отличие от последовательности Фибоначчи, которую мы видели на вводном посте , проблему, которую я здесь представляю, решить немного сложнее (что также делает ее более интересной).
Причина, по которой я расскажу об этой и других подобных проблемах в будущих публикациях, заключается не только в том, чтобы показать, как их решить. Любой, кто имеет доступ к Google, может найти одно из 100 уже реализованных решений. Идея здесь состоит в том, чтобы показать некоторые ключевые концепции, которые можно применить к любой динамической проблеме.
Итак, давайте начнем с хорошо известной проблемы редактирования расстояния . По сути, для двух строк A и B расстояние редактирования измеряет минимальное количество операций, необходимых для преобразования одной строки в другую. В самой распространенной версии этой проблемы мы можем применить 3 различные операции:
- Вставьте новый символ в одну из строк
- Удалить существующего персонажа
- Заменить одного персонажа другим
Например, учитывая строки A = «cat» и B = «cars» , editDistance (A, B) = 2, потому что минимальное количество преобразований, которое нам нужно сделать, это заменить «t» в A на «r» и затем удалите «с» из B. После этого обе строки равны «машине». Обратите внимание, что в этом случае другой возможностью было бы заменить букву «t» буквой «r», но затем вставить букву «s» в A , чтобы обе строки были равны «cars». Точно так же мы могли бы изменить и на «кошку» или на «кошку», и расстояние редактирования все равно 2.
Итак, как бы мы решили эту проблему? Давайте попробуем решить гораздо меньшую и более простую проблему. Представьте, что у нас снова есть две предыдущие строки, на этот раз представленные в виде массива символов в общем виде:
A = [A0, A1, A2,…, An]
B = [B0, B1, B2,…, Bm]
Обратите внимание, что длины A и B (n и m соответственно) могут быть разными.
Мы знаем, что в конце обе строки должны иметь одинаковую длину и совпадать со своими символами в каждой позиции. Итак, если мы возьмем только первый символ A и B , какой у нас будет выбор? У нас есть 3 различных преобразования, которые мы можем применить, поэтому у нас также есть 3 варианта:
- Мы можем заменить первый символ A первым символом B. Стоимость такой замены будет 1, если символы разные, и 0, если они равны (потому что в этом случае нам ничего не нужно делать). На данный момент мы знаем, что обе строки начинаются с одного и того же символа, поэтому мы можем вычислить расстояние редактирования для A [1..n] = [A1,…, An] и B [1..m] = [B1,…, Бм] . Конечным результатом будет стоимость преобразования A [0] в B [0] плюс расстояние редактирования оставшихся подстрок.
- Второй выбор, который у нас есть, это вставка символа в A для соответствия символу в B [0] , стоимость которого равна 1. После того, как мы это сделали, нам все еще нужно рассмотреть исходную строку A, потому что мы добавили новый символ к нему, но мы не обработали ни одного из его оригинальных персонажей. Однако нам больше не нужно рассматривать B [0] , потому что мы знаем, что он соответствует A [0] в этой точке. Поэтому единственное, что нам нужно сделать сейчас, — это вычислить расстояние редактирования оригинала A и B [1..m] = [B1,…, Bm] . Конечным результатом будет это значение плюс 1 (стоимость вставки символа в A).
- Последний случай симметричен предыдущему. Третье преобразование, которое мы можем применить, — это просто удалить A [0] . Эта операция также имеет стоимость 1. После этого мы использовали один символ A, но у нас все еще есть все оригинальные символы B для обработки. Поэтому нам просто нужно вычислить расстояние редактирования для A [1..n] = [A1,…, An] и B. Опять же, окончательным значением расстояния редактирования будет это значение плюс 1 (стоимость удаления A [0] .
Так какой из трех вариантов мы должны выбрать изначально? Ну, на самом деле мы не знаем, какой из них будет лучше в итоге, поэтому мы должны попробовать их все. Ответом на нашу первоначальную проблему будет минимальное значение этих трех альтернатив.
Предыдущее описание является ключом к решению этой проблемы, поэтому прочитайте его еще раз, если неясно. Обратите внимание, что последний шаг в каждой из трех альтернатив включает вычисление расстояния редактирования 2 подстрок A и B. Это та же самая проблема, что и оригинальная, которую мы пытаемся решить, то есть решение расстояния редактирования для 2 строк. Разница в том, что после каждого принятого нами решения проблема становится меньше, потому что одна или обе входные строки становятся меньше. Мы решаем исходную проблему, решая меньшие подзадачи одного и того же типа . Тот факт, что подзадачи становятся меньше на каждом шаге, крайне важен, чтобы быть уверенным, что в какой-то момент мы завершим алгоритм. В противном случае мы могли бы продолжать решать подзадачи бесконечно.
Так, когда мы прекращаем решать подзадачи? Мы можем остановиться, как только дойдем до случая, который тривиально решить: базовый случай. В нашем случае это когда одна или обе входные строки пусты. Если обе строки пусты, то расстояние редактирования между ними равно 0, потому что они уже равны. В противном случае расстояние редактирования будет длиной строки, которая не является пустой. Например, чтобы преобразовать «aab» в «», мы можем либо удалить 3 символа из первой строки, либо вставить их во вторую строку. В любом случае расстояние редактирования составляет 3.
До сих пор мы определяли решение нашей проблемы с точки зрения решения меньшей подзадачи того же типа и определяли базовый случай, когда мы уже знаем, каков результат. Это должно быть четким указанием на то, что рекурсивный алгоритм может быть применен.
Но сначала давайте переведем три варианта, описанных ранее, описывающих взаимосвязь между подзадачами, во что-то, что будет более полезным при попытке закодировать это. Отношение повторения может быть определено как:
Первый случай предыдущей формулы — когда мы заменяем A [0] на B [0] , второй — когда мы удаляем A [0], а последний — когда мы вставляем в A. Базовые случаи:
Обратите внимание, что случай, когда обе строки пусты, уже охватывается первым базовым случаем, потому что length (A) == length («») == 0 .
Перевести это определение в рекурсивный алгоритм относительно просто:
|
01
02
03
04
05
06
07
08
09
10
11
12
|
public class BruteForceEditDistance implements EditDistance { public int editDistance(String word1, String word2) { if (word1.isEmpty()) return word2.length(); if (word2.isEmpty()) return word1.length(); int replace = editDistance(word1.substring(1), word2.substring(1)) + Util.replaceCost(word1, word2, 0, 0); int delete = editDistance(word1.substring(1), word2) + 1; int insert = editDistance(word1, word2.substring(1)) + 1; return Util.min(replace, delete, insert); }} |
У класса Util есть несколько полезных методов, которые мы будем использовать в различных реализациях алгоритма, и он выглядит примерно так:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
|
public class Util { /** * Prevent instantiation */ private Util(){} public static int replaceCost(String w1, String w2, int w1Index, int w2Index) { return (w1.charAt(w1Index) == w2.charAt(w2Index)) ? 0 : 1; } public static int min(int... numbers) { int result = Integer.MAX_VALUE; for (int each : numbers) { result = Math.min(result, each); } return result; }} |
Код выглядит сжатым и дает ожидаемый ответ. Но, как вы, вероятно, можете себе представить, учитывая, что мы говорим о динамическом программировании, этот метод грубой силы далеко не эффективен. Как и в примере с Фибоначчи, который мы видели в последнем посте, этот алгоритм вычисляет один и тот же ответ несколько раз, вызывая экспоненциальный взрыв различных путей, которые нам нужно исследовать.
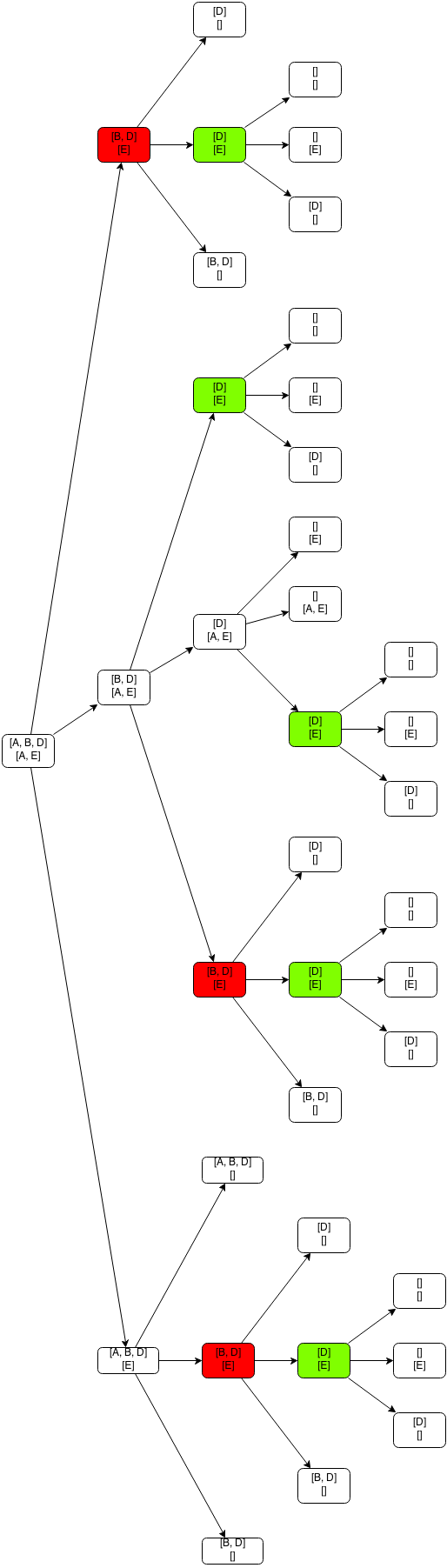
Чтобы увидеть это, давайте рассмотрим последовательность вызовов, которые выполняются, когда мы вызываем этот метод с word1 = «ABD» и word2 = «AE» :
И это только для двух строк длиной 3 и 2. Представьте, как выглядит эта картинка, когда у вас есть подходящие слова или даже предложения. В моем ноутбуке для любых двух строк с 10 или более символами метод никогда не заканчивается. Этот подход явно не будет масштабироваться.
Итак, можем ли мы применить динамическое программирование к этой проблеме? Вспомните два основных свойства динамической задачи, которые мы обсуждали в предыдущем посте : перекрывающиеся подзадачи и оптимальная подструктура. Как мы только что видели на примере предыдущего рисунка, проблема с расстоянием редактирования явно имеет перекрывающиеся подзадачи, потому что мы решаем меньшие подзадачи того же типа, чтобы получить окончательное решение, и нам нужно решить те же подзадачи многократно.
Как насчет оптимальной подструктуры? Можем ли мы вычислить оптимальное решение, если у нас есть оптимальные решения для подзадач? Конечно! В нашем случае мы пытаемся минимизировать количество преобразований, поэтому, если у нас есть оптимальное решение для трех рассматриваемых нами случаев (заменить, вставить и удалить), мы получим минимум из этих трех, и это наше оптимальное решение.
Помните из предыдущего поста, что у нас может быть подход динамического программирования «сверху вниз», где мы запоминаем рекурсивную реализацию или подход «снизу вверх». Последнее имеет тенденцию быть более эффективным, потому что вы избегаете рекурсивных вызовов. Что еще более важно, выбор между этими двумя может быть разницей между рабочим и нерабочим алгоритмом, если число рекурсивных вызовов, которые вам нужно сделать, чтобы добраться до базового случая, слишком велико. Если это не проблема, то выбор того, который использовать, обычно зависит от личных предпочтений или стиля. Вот возможный алгоритм сверху вниз:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
public class DPMemoizedEditDistance implements EditDistance { public int editDistance(String word1, String word2) { return editDistance(word1, word2, new HashMap<StringTuple, Integer>()); } private int editDistance(String word1, String word2, Map<StringTuple, Integer> computedSolutions) { if (word1.isEmpty()) return word2.length(); if (word2.isEmpty()) return word1.length(); StringTuple replaceTuple = new StringTuple(word1.substring(1), word2.substring(1)); StringTuple deleteTuple = new StringTuple(word1.substring(1), word2); StringTuple insertTuple = new StringTuple(word1, word2.substring(1)); int replace = Util.replaceCost(word1, word2, 0, 0) + transformationCost(replaceTuple, computedSolutions); int delete = 1 + transformationCost(deleteTuple, computedSolutions); int insert = 1 + transformationCost(insertTuple, computedSolutions); int minEditDistance = Util.min(replace, delete, insert); computedSolutions.put(new StringTuple(word1, word2), minEditDistance); return minEditDistance; } private int transformationCost(StringTuple tuple, Map<StringTuple, Integer> solutions) { if (solutions.containsKey(tuple)) return solutions.get(tuple); int result = editDistance(tuple.s1, tuple.s2, solutions); solutions.put(tuple, result); return result; } /** * Helper class to save previous solutions * */ private class StringTuple { private final String s1; private final String s2; public StringTuple(String s1, String s2) { this.s1 = s1; this.s2 = s2; } @Override public int hashCode() { return HashCodeBuilder.reflectionHashCode(this); } @Override public boolean equals(Object obj) { return EqualsBuilder.reflectionEquals(this,obj); } }} |
Давайте посмотрим, что здесь происходит. Прежде всего, мы используем карту для хранения вычисленных решений. Поскольку входные данные для нашего метода представляют собой две строки, мы создали вспомогательный класс с двумя строками, который будет служить ключом для карты . Наш открытый метод имеет тот же интерфейс, что и раньше, получая 2 входа и возвращая расстояние. В этой запомненной версии мы создаем карту здесь и делегируем вычисление частному методу, который будет выполнять необходимые рекурсивные вызовы. Этот закрытый метод будет использовать карту computedSolutions, чтобы избежать дублирования работы. Остальная часть алгоритма работает точно так же, как и метод грубой силы, который мы видели ранее. На каждом шаге мы вычисляем (или получаем результат, если он уже был рассчитан) расстояние редактирования для трех различных возможностей: заменить, удалить и вставить. Теперь после вычисления этих расстояний мы сохраняем их, берем их минимум, сохраняем результат для исходного ввода и возвращаем его.
Этот алгоритм является огромным улучшением по сравнению с наивным рекурсивным алгоритмом, который мы видели ранее. Просто чтобы привести пример, тот же самый вызов, который никогда не завершался, теперь занимает 0,075 секунды. Преимущество этого подхода в том, что мы можем повторно использовать рекурсивный метод, который у нас уже был, с некоторыми незначительными изменениями. Плохая часть в том, что мы проводим много сравнений и манипуляций со строками, и это имеет тенденцию быть медленным.
Поскольку две строки, которые мы получаем в качестве входных данных, могут быть большими, давайте попробуем использовать восходящий подход:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
public class DPBottomUpEditDistance implements EditDistance { public int editDistance(String word1, String word2) { if (word1.isEmpty()) return word2.length(); if (word2.isEmpty()) return word1.length(); int word1Length = word1.length(); int word2Length = word2.length(); //minCosts[i][j] represents the edit distance of the substrings //word1.substring(i) and word2.substring(j) int[][] minCosts = new int[word1Length][word2Length]; //This is the edit distance of the last char of word1 and the last char of word2 //It can be 0 or 1 depending on whether the two are different or equal minCosts[word1Length - 1][word2Length - 1] = Util.replaceCost(word1, word2, word1Length - 1, word2Length - 1); for (int j = word2Length - 2; j >= 0; j--) { minCosts[word1Length - 1][j] = 1 + minCosts[word1Length - 1][j + 1]; } for (int i = word1Length - 2; i >= 0; i--) { minCosts[i][word2Length - 1] = 1 + minCosts[i + 1][word2Length - 1]; } for (int i = word1Length - 2; i >= 0; i--) { for (int j = word2Length - 2; j >= 0; j--) { int replace = Util.replaceCost(word1, word2, i, j) + minCosts[i + 1][j + 1]; int delete = 1 + minCosts[i + 1][j]; int insert = 1 + minCosts[i][j + 1]; minCosts[i][j] = Util.min(replace, delete, insert); } } return minCosts[0][0]; }} |
Здесь мы создаем матрицу для хранения значений расстояний редактирования различных подстрок. Вместо того, чтобы хранить ссылки на все разные подстроки, как мы делали в записанной версии, мы просто сохраняем 2 индекса. Таким образом, minCosts [i] [j] — это значение для расстояния редактирования между word1 [i..n] и word2 [j..m] . Учитывая эту структуру, что является наименьшей проблемой, решение которой тривиально? Тот, который рассматривает два последних символа каждой строки: если оба символа равны, то их расстояние редактирования равно 0, иначе равно 1.
Давайте рассмотрим алгоритм на оригинальном примере «кошка» и «автомобили», чтобы лучше понять, как он работает. Предположим, слово1 = и слово2 = , Тогда наша матрица будет иметь размер 3 × 4 со всеми местами, изначально установленными на 0:
Далее мы сравним два последних символа обеих строк, поэтому «t» и «s». Поскольку они разные, мы обновляем minCosts [2] [3] на 1:
Получив это значение, мы можем рассчитать все остальные значения для последней строки и последнего столбца. Например, что означает minCosts [2] [2] ? Согласно нашему определению это расстояние редактирования между word1 [2..2] и word2 [2..3] , которое в нашем случае означает расстояние редактирования между «t» и «rs». Но так как мы уже знаем, что расстояние редактирования между «t» и «s» равно 1 (потому что мы можем искать это значение в матрице), любая дополнительная буква, которую мы добавляем ко второй строке, оставляя при этом первую фиксированную, может только увеличить расстояние на 1. Таким образом, minCosts [2] [2] равно minCosts [2] [3] + 1 , minCosts [2] [1] равно minCosts [2] [2] + 1 и minCosts [2] [ 0] равно minCosts [2] [1] + 1 .
Те же рассуждения применимы, если мы оставим столбец фиксированным и перейдем вверх по строкам. После этих двух начальных циклов наша матрица выглядит так:
Теперь мы можем легко заполнить нашу матрицу, следуя формуле повторения, которую мы определили в начале. Для каждой ячейки нам понадобится значение ячейки справа от нее, ячейка прямо под ней и ячейка справа от нее. Таким образом, мы можем пройти матрицу снизу вверх и справа налево. Применяя формулу повторения к minCosts [1] [2], например, мы получаем, что ее значение равно 2. С этим значением мы можем вычислить minCosts [1] [1] , minCosts [1] [0] и значения для первого ряд. Наша окончательная матрица:
Итак, теперь, когда мы заполнили всю нашу матрицу, каков ответ на нашу первоначальную проблему? Помните еще раз, что minCosts [i] [j] — это значение для расстояния редактирования между word1.substring (i) и word2.substring (j) . Таким образом, поскольку word1.substring (0) == word1 , наш окончательный ответ — это значение minCosts [0] [0] .
Каковы преимущества этого восходящего подхода по сравнению с запомненной версией? Во-первых, нам не нужны рекурсивные вызовы. Наша реализация — полностью итеративный метод, который просто пересекает матрицу. Во-вторых, нам не нужно отслеживать все возможные подстроки и оперировать ими. Мы просто используем индексы матрицы для представления подстрок, что значительно быстрее.
В заключение этой статьи, давайте вспомним, что мы сделали, чтобы решить эту проблему:
- Мы определили, что можем решить исходную проблему, разбив ее на более мелкие подзадачи того же типа.
- Мы предполагали, что каким-то образом знаем, каковы ответы на подзадачи, и думали о том, как мы будем использовать эти ответы, чтобы получить ответ на исходную проблему.
- На предыдущем этапе мы определили общую формулу повторения, которая представляла отношения между различными подзадачами. Эта повторяющаяся формулировка обычно является наиболее важной частью решения формулы динамического программирования. Получив его, перевести это в алгоритм обычно просто
- Мы реализовали наивное рекурсивное решение и определили, что решаем одни и те же подзадачи снова и снова
- Мы изменили предыдущее решение, чтобы сохранить и повторно использовать результаты, используя запомненный рекурсивный метод
- Мы определили, что рекурсивные вызовы могут быть проблемой для длинных строк, и поэтому мы разработали подход снизу вверх. В этой версии мы определили матрицу для хранения результатов и выяснили, каким образом нам нужно ее заполнить, используя точно такую же формулу повторения, определенную ранее
Вы можете найти все реализации, которые мы видели здесь, вместе с автоматическими тестами для каждой из них, показывающими различия во времени выполнения, на https://github.com/jlordiales/edit-distance
В следующих постах мы увидим, что эти же шаги можно применить с небольшими изменениями для огромного количества различных проблем. Как только вы ознакомитесь с основными советами и приемами динамического программирования, большинство проблем станут похожими.
Ура !!!