Вау, я давно уже ничего не писал. Между сменой работы, работой над докторской диссертацией и переездом в новую страну, я думаю, можно сказать, что я был довольно занят.
Но в то же время, вместе со всеми этими изменениями в моей жизни, есть масса новых вещей, которые я изучаю почти каждый день. И, как и многие другие , я чувствую, что писать о них так, чтобы другим было легко их понять, — это один из лучших способов закрепить мое собственное обучение. Так что теперь я буду стараться писать здесь чаще.
Итак, с этим рассмотрено, давайте перейдем к важным вещам. По какой-то причине в последнее время я очень заинтересовался обновлением старых концепций из алгоритмов и структур данных, которые были немного ржавыми. Вместе с этими старыми концепциями также появились новые концепции и методы, о которых я никогда не слышал раньше. Но я буду обращаться к ним по отдельным постам.
В этом посте я хотел поговорить о динамическом программировании. Если вы когда-нибудь проходили университетский курс по алгоритмам, вы, вероятно, слышали об этом. Если вы этого не сделали, у вас есть хороший шанс узнать что-то чрезвычайно полезное, простое и интуитивно понятное (по крайней мере, когда вы это правильно понимаете).
Так что же такое динамическое программирование? Я не буду вдаваться в подробности теории, потому что вы уже можете найти все это, если сделаете простой поиск в Google. Я определю это как «умную рекурсию» и, как обычно, поясню это на примере.
Классическим примером для объяснения динамического программирования является вычисление Фибоначчи , так что я тоже пойду с этим. Определение числа Фибоначчи числа явно рекурсивное:
F (n) = F (n-1) + F (n-2) и F (1) = F (2) = 1
Это означает, что последовательность первых 10 чисел Фибоначчи будет иметь вид:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55
Вы также можете найти его определенным как:
F (0) = F (1) = 1
И так последовательность будет:
0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55
Для целей этого поста это различие не имеет значения, но я остановлюсь на первом.
Теперь это рекурсивное определение естественно и довольно аккуратно переводится в следующий рекурсивный метод:
|
1
2
3
4
|
public static long fibonacci(int n) { if (n < 3) return 1; return fibonacci(n-2) + fibonacci(n-1);} |
Вы даже можете сделать это одним вкладышем:
|
1
2
3
|
public static long fibonacci(int n) { return (n < 3) ? 1 : fibonacci(n-2) + fibonacci(n-1);} |
Теперь этот метод работает, и он, безусловно, элегантен, но, что происходит со временем выполнения, когда вы начинаете увеличивать параметр n . Ну, в моем ноутбуке он возвращается почти сразу для любого значения от 0 до 30. Для n из 40 это занимает немного больше времени: 0,5 секунды. Но для n, равного 50, для вычисления правильного значения требуется почти полная минута.
Вы можете подумать, что полная минута — это не много, но любое значение больше 70 убивает приложение для меня, а любое значение от 50 до 70 занимает слишком много времени, чтобы закончить. Сколько? Я действительно не знаю, потому что у меня нет терпения ждать и видеть, но это определенно больше, чем 30 минут.
Так что же не так с этим методом? Ну, я еще не говорил о сложности времени и пространства алгоритмов (я, вероятно, расскажу об этом в другом посте), поэтому сейчас я просто скажу, что время выполнения алгоритма растет экспоненциально с ростом n . Вот почему существует такая большая разница во времени, когда вы выполняете этот метод с n = 40 и с n = 50 , потому что есть огромная разница между 2 ^ 40 и 2 ^ 50.
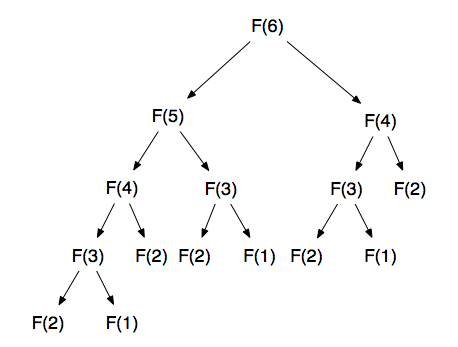
Причину, по которой этот алгоритм ведет себя так, также довольно легко увидеть, просто следуя его стеку выполнения для любого значения n . Давайте сделаем это для n = 6, чтобы оно было коротким. На следующем рисунке показана последовательность звонков.
Глядя на код, мы можем ясно видеть, что для вычисления значения для 6 мы сначала вычисляем значения для 5 и 4. Но, аналогично, для вычисления значения 5 нам нужны значения для 4 и 3 и для вычисления значений для 4 нам нужны значения для 3 и 2. Как только мы доберемся до 2, мы можем закончить рекурсию, потому что мы знаем результат (который равен 1).
И вот проблема с этим методом, обратите внимание, сколько раз мы вызываем fibonacci (4) и сколько раз мы вызываем fibonacci (3). Это полностью дублированная работа, которую мы делаем. Зачем рассчитывать одни и те же результаты снова и снова, если они никогда не изменятся? Как только мы рассчитали Фибоначчи (3) или Фибоначчи (4) в первый раз, мы можем сохранить этот результат и использовать его всякий раз, когда нам нужно.
И это именно то, что я имел в виду под умной рекурсией. У вас может быть естественное и простое рекурсивное решение, но вам нужно определить такие ситуации, когда вы повторяете работу, и избегать их. Для n = 6 это не было таким уж большим делом, но с ростом n количество дублируемой работы также растет в геометрической прогрессии, пока не сделает приложение бесполезным.
Итак, как мы можем улучшить это? Нам нужно только сохранить ранее вычисленные значения, и мы можем использовать любую структуру, которую мы хотим для этого. В этом случае я просто буду использовать карту:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
|
public static long fibonacci(int n) { if (n < 3) return 1; //Map to store the previous results Map<Integer,Long> computedValues = new HashMap<Integer, Long>(); //The two edge cases computedValues.put(1, 1L); computedValues.put(2, 1L); return fibonacci(n,computedValues);}private static long fibonacci(int n, Map<Integer, Long> computedValues) { if (computedValues.containsKey(n)) return computedValues.get(n); computedValues.put(n-1, fibonacci(n-1,computedValues)); computedValues.put(n-2, fibonacci(n-2,computedValues)); long newValue = computedValues.get(n-1) + computedValues.get(n-2); computedValues.put(n, newValue); return newValue;} |
Эта версия, очевидно, немного длиннее первой, но все еще довольно проста для понимания. Теперь у нас есть 2 метода: основной публичный, который клиенты вызывают только с параметром n, и закрытый, который выполняет рекурсивные вызовы. Первый метод — полезное место для инициализации всей необходимой информации, которую мы должны вызвать для второго. Это довольно распространенный шаблон при работе с рекурсивными алгоритмами.
В этом случае мы используем карту для хранения уже вычисленных результатов. Мы инициализируем эту карту с 2 базовыми случаями в первом методе, а затем вызываем второй метод с этой картой. Теперь вместо того, чтобы всегда вычислять значение, мы сначала проверяем, есть ли оно уже на карте. Если это так, мы просто возвращаем это значение, в противном случае мы вычисляем и сохраняем число Фибоначчи для n-1 и n-2 . Перед возвратом их суммы мы сохраняем окончательное значение n .
Обратите внимание, что мы все еще следуем той же структуре, что и первый метод, который мы видели. То есть мы начинаем с n и вычисляем меньшие результаты по мере необходимости, чтобы решить исходную проблему. Вот почему этот подход называется сверху вниз. Позже мы увидим подход снизу вверх и сравним оба. Этот метод следования нисходящему подходу и сохранения ранее вычисленных результатов также известен как запоминание .
Насколько лучше эта версия? Что ж, в то время как первая версия потребовала почти минуту, чтобы вычислить значение для n = 50 и никогда не заканчивалась для значений выше этого, вторая запомненная версия дает мгновенный ответ для любого n до 7000. Это огромное улучшение, но, как обычно мы можем сделать лучше.
Проблема с этой новой запомненной версией состоит в том, что даже когда мы сохраняем результаты, чтобы использовать их позже, нам все равно нужно пройти весь путь до базового случая с рекурсией в первый раз (когда мы не вычислили никаких значений пока и так у нас ничего не хранится). Итак, представьте, что мы вызываем метод с n = 10000. Поскольку у нас пока нет этого результата, мы вызываем метод рекурсивно с 9999, 9998, 9997,…, 2. После того, как мы начнем возвращаться из рекурсии, все n-2 значения, которые нам нужны, будут уже там, так что эта часть довольно быстрая.
Как и в любом рекурсивном алгоритме, каждый рекурсивный вызов занимает некоторое место в стеке. И, если у нас будет достаточно этих рекурсивных вызовов, стек в конечном итоге взорвется, создав исключение StackOverflowException . И это именно то, что происходит с нашим вторым методом, когда мы используем значения более 10000.
Итак, какова альтернатива? Я упоминал ранее, что запомненная версия следовала нисходящему подходу. Очевидное, что нужно сделать, это пойти в противоположном направлении восходящим образом. Начиная с небольших значений n и наращивая результаты до нашей цели. Мы все еще сохраним уже вычисленные значения, чтобы использовать их на более поздних этапах и избежать дублирования работы. Это решение выглядит примерно так:
|
1
2
3
4
5
6
7
8
9
|
public static long fibonacciDP(int n) { long[] results = new long[n+1]; results[1] = 1; results[2] = 1; for (int i = 3; i <= n; i++) { results[i] = results[i-1] + results[i-2]; } return results[n];} |
Это на самом деле выглядит проще, чем наша запоминающаяся версия. Мы просто создаем массив для хранения результатов, инициализируем его двумя базовыми вариантами, а затем начинаем итерацию с 3 до n . На каждом шаге мы используем 2 ранее вычисленных значения для вычисления текущего. В конце мы возвращаем правильное значение для n .
По сложности и количеству вычислений эта версия точно такая же, как и вторая. Разница здесь в том, что последняя версия является итеративной и, следовательно, не занимает место в стеке как рекурсивная. Теперь мы можем вычислить последовательность Фибоначчи до n = 500000 или более, и время отклика практически мгновенно.
Но мы еще не совсем закончили, есть еще одна вещь, которую мы можем улучшить. Хотя мы пошли от экспоненциальной к линейной сложности времени, мы также увеличили объем требуемого пространства. В двух последних версиях алгоритма пространство, необходимое для хранения предыдущих решений, пропорционально n . Это, вероятно, довольно ясно в нашем последнем методе, где мы создали массив длиной n . Чем больше n, тем больше места нам нужно.
Но на самом деле вы можете видеть, что единственные два значения, которые нам когда-либо нужны, это последние два ( n-1 и n-2 ). Поэтому нам не нужно отслеживать все предыдущие решения, только последние два. Мы можем изменить последний метод, чтобы сделать это:
|
01
02
03
04
05
06
07
08
09
10
11
|
public static long fibonacciDP(int n) { long n1 = 1; long n2 = 1; long current = 2; for (int i = 3; i <= n; i++) { current = n1 + n2; n2 = n1; n1 = current; } return current;} |
Здесь мы заменили массив длины n всего тремя переменными: текущим и двумя предыдущими значениями. Итак, последний метод имеет линейную временную сложность и постоянную пространственную сложность, потому что количество переменных, которые мы должны объявить, не зависит от размера n .
И это так хорошо, как мы можем получить с помощью динамического программирования. На самом деле есть алгоритм логарифмической сложности, но я не буду обсуждать его здесь.
Так что, как мы могли видеть из этих примеров, в динамическом программировании нет ничего загадочного или сложного. Требуется только проанализировать исходное решение, определить места, где вы выполняете дублированную работу, и избежать этого, сохраняя уже рассчитанные результаты. Эта очень простая оптимизация позволяет перейти от экспоненциального решения, которое является неизменным для большинства практических входных значений, к полиномиальному решению. В частности, вы хотите найти 2 отличительные характеристики проблем, которые могут быть решены с помощью динамического программирования: перекрывающиеся подзадачи и оптимальная подструктура .
Перекрывающиеся подзадачи относятся к природе таких проблем, как последовательность Фибоначчи, которую мы видели здесь, где основная проблема (вычисление фибоначчи от n ) может быть решена путем решения меньших подзадач, и необходимы решения этих меньших подзадач. снова и снова. Это в тех случаях, когда имеет смысл сохранить результаты и использовать их позже.
Однако, если подзадачи полностью независимы, и нам нужны их результаты только один раз, тогда нет смысла их сохранять. Примером проблемы, которая может быть разделена на подзадачи, но где эти подзадачи не перекрываются, является бинарный поиск . Как только мы отбрасываем половину, которая нас не волнует, мы никогда не посещаем ее снова.
Оптимальная подструктура тесно связана, и это в основном означает, что оптимальное решение может быть эффективно построено из оптимальных решений его подзадач. Это свойство не было так очевидно в примере Фибоначчи, потому что есть только 1 решение для любого данного n . Но это будет более очевидно в будущих примерах, связанных с какой-либо оптимизацией.
Я завершу этот пост некоторыми советами, которые я использую, пытаясь решить, использовать ли динамическое программирование для данной проблемы:
- Можно ли разделить проблему на подзадачи того же рода?
- Могу ли я определить предыдущее деление по определению повторения? То есть определить F (n) как функцию от F (n-1)
- Нужны ли результаты для подзадач несколько раз или только один раз?
- Есть ли смысл использовать нисходящий или восходящий подход?
- Нужно ли беспокоиться о стеке, если я использую запомненный рекурсивный подход?
- Нужно ли сохранять все предыдущие результаты или я могу оптимизировать пространство и оставить только некоторые из них?
В следующих статьях я расскажу о некоторых классических и довольно интересных проблемах, которые можно эффективно решить с помощью динамического программирования.
Ура!