Функциональный стиль — часть 8

Постоянные структуры данных.

Мы уже давно обсуждали неизменность. В частности, мы рассмотрели, как циклы можно заменить рекурсивными вызовами функций для выполнения итерации, избегая переназначения любых переменных. Хотя на первый взгляд может показаться, что этот метод будет крайне неэффективным с точки зрения памяти, мы видели, как устранение хвостовых вызовов может свести на нет необходимость в дополнительных вызовах подпрограмм, тем самым избегая увеличения стека вызовов и делая функциональные алгоритмы практически идентичными их императивные эквиваленты на уровне машины.

Так много для скалярных значений, но как насчет сложных структур данных, таких как массивы и словари? В функциональных языках они тоже неизменны. Поэтому, если у нас есть список в Clojure:

и мы создаем новый список, добавляя к нему элемент:

тогда у нас теперь есть два списка, один из которых равен (1 2 3) а другой (0 1 2 3) . Означает ли это, что для того, чтобы изменить структуру данных в функциональном стиле, мы должны сделать полную копию оригинала, чтобы сохранить ее без изменений? Это казалось бы крайне неэффективным.

Тем не менее, существуют способы, позволяющие сделать структуры данных изменяемыми, сохраняя при этом исходный код без изменений для любых частей программы, которые все еще содержат ссылки на него. Такие структуры данных называются «постоянными», в отличие от «эфемерных» структур данных, которые являются изменчивыми. Структуры данных полностью сохраняются, когда каждая версия структуры может быть изменена, и этот тип мы обсудим здесь. Структуры частично сохраняются, когда только самая последняя версия может быть изменена.

Полностью сложены.

Стек является очень хорошим примером того, как реализовать постоянную структуру данных, потому что он также показывает дополнительное преимущество этого метода. Код тоже становится проще; мы придем к этому через минуту.

Поскольку мы создаем здесь функциональный стек, наш интерфейс выглядит следующим образом:

Учитывая, что это постоянная структура данных, мы никогда не сможем изменить ее, поэтому при нажатии или выталкивании мы получаем новый экземпляр Stack который отражает наш вытолкнутый или вытолкнутый стек. Любые части программы, которые содержат ссылки на предыдущие состояния стека, будут продолжать видеть это состояние без изменений.

Для получения нового стека мы предоставим статический метод фабрики:

Может показаться странным выбор дизайна для создания конкретной реализации для пустого стека, но когда мы это делаем, все получается очень аккуратно. Это преимущество, которое я упоминал ранее:

Как видите, top возвращает пустое значение, а pop генерирует исключение из недопустимого состояния. Я думаю, что в этом случае разумно создать исключение, потому что, учитывая природу стеков « первым пришел — первым вышел», и их типичное использование, любая попытка вытолкнуть пустой стек указывает на вероятную ошибку в программе, а не на ошибку пользователя.

Что касается непустой реализации, это выглядит так:

Стоит отметить, что выбор отдельных реализаций для пустых и непустых случаев исключает необходимость какой-либо условной логики. В приведенном выше коде нет операторов if .

При использовании стек ведет себя так:

1. Stack.create возвращает экземпляр EmptyStack .
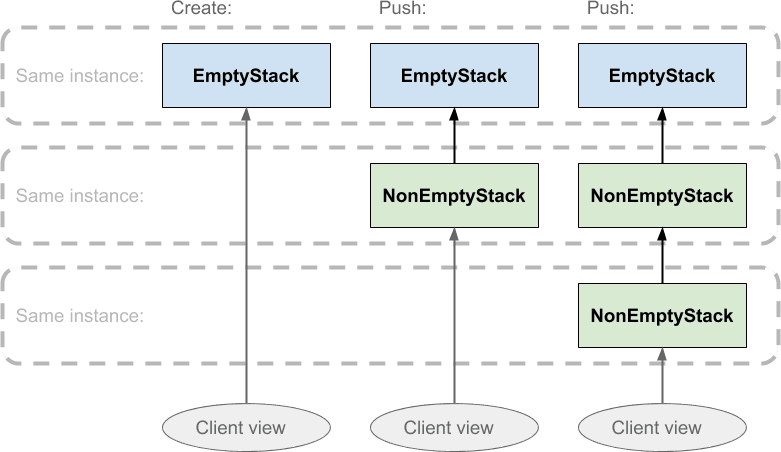
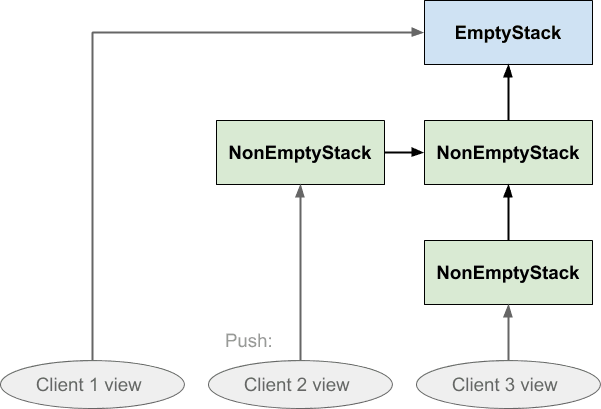
2. Нажатие на него возвращает NonEmptyStack с NonEmptyStack значением в качестве его вершины.
3. Когда другое значение помещается поверх непустого стека, создается еще один экземпляр NonEmptyStack с новым добавленным значением сверху:

Временная шкала здесь проходит слева направо, а овалы внизу диаграммы представляют «вид» стека, который видит клиент. Области, ограниченные пунктирными линиями, указывают на то, что все блоки внутри одного экземпляра объекта. Направление стрелок показывает, что каждый экземпляр NonEmptyStack содержит ссылку на другой экземпляр стека, его родитель, который будет либо пустым, либо непустым. Эта ссылка на родительский объект — это то, что будет возвращено при извлечении стека, и именно здесь все станет умнее:

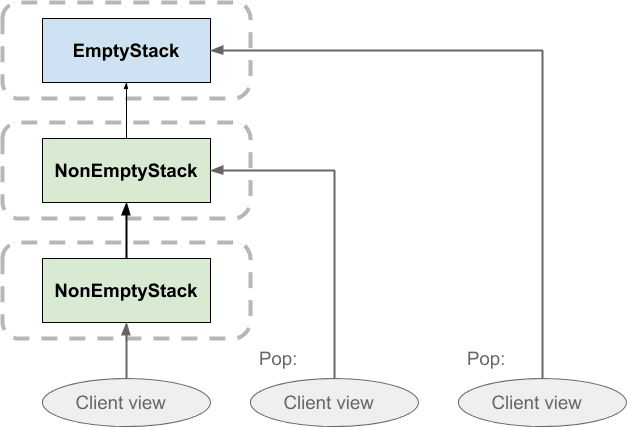
При извлечении стека клиент просто переключает свой взгляд на ранее помещенный элемент. Ничто не удаляется. Это означает, что, если бы два клиента имели один и тот же стек, один клиент мог бы извлечь его, не влияя на представление другого стека. То же самое верно для толкания:

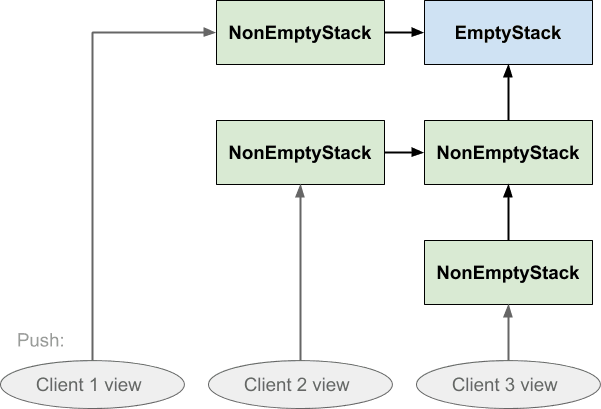
Это в основном то же самое, что и первая диаграмма, за исключением того, что мы обошлись без горизонтальных пунктирных областей и вместо этого сделали явным, что стек представляет собой одну структуру данных, а не несколько копий. Мы просто представляем каждый экземпляр Stack , независимо от того, пустой он или нет, как один блок. Первоначально клиент видит пустой стек; при нажатии создается непустой стек, который указывает на пустой стек, и клиент переключает свой взгляд на новый экземпляр. Когда клиент нажимает второй раз, создается другой непустой стек, который указывает на предыдущий непустой стек, и клиент снова меняет свое представление. Стек сообщает клиенту, куда направить его представление, через возвращаемое значение операций push и pop, но именно клиент фактически меняет свое представление. Стек ничего не двигает.

Теперь вы можете подумать, что «клиент меняет свое представление» подразумевает, что что- то мутирует, и это действительно так, но это просто переменная, содержащая ссылку на экземпляр стека. Мы уже подробно обсуждали во второй части серии, как управлять изменением скалярных значений без переназначения переменных.

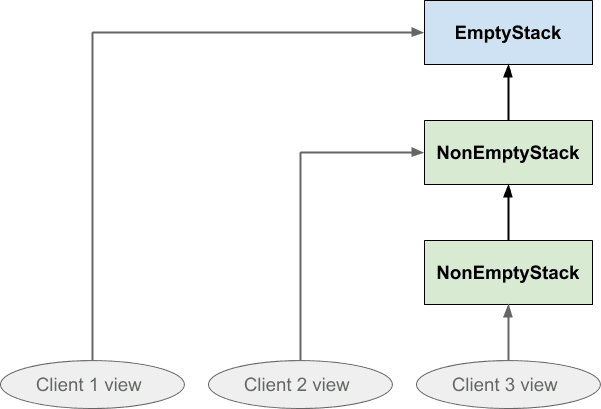
Мы уже упоминали о возможности того, что разные части программы могут содержать отдельные и разные представления о структуре стека, поэтому теперь давайте явно представим, что три овала представляют три разных представления клиентов об одной структуре стека. Клиент 1 смотрит на вновь созданный стек, клиент 2 нажал на него один раз, а клиент 3 нажал на него дважды:

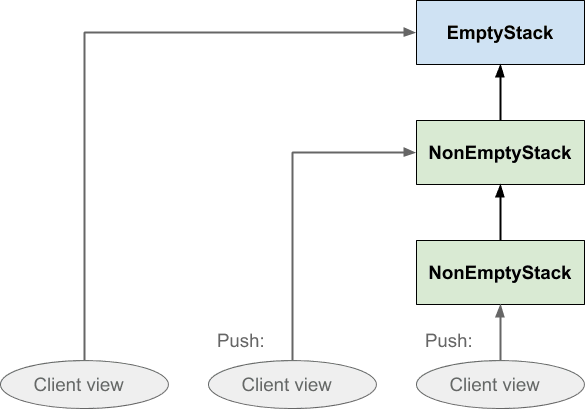
Если клиент 2 впоследствии поместит что-либо в стек, эффект будет выглядеть следующим образом:

Обратите внимание, что направления стрелок гарантируют, что ни клиент 1, ни клиент 3 не будут затронуты тем, что сделал клиент 2: клиент 3 не может следовать за стрелкой назад, чтобы увидеть значение, которое было только что нажато, и не может клиент 1. Аналогично, если клиент 1 нажал на стек ни один из остальных не будет затронут этим:

Еще одна вещь, которую стоит отметить в этой структуре данных, это то, что ничего не дублируется. Все три клиента совместно используют один и тот же экземпляр EmptyStack, а клиенты 2 и 3 также совместно используют NonEmptyStack, который был передан первым. Все, что может быть передано, является общим. Ничто не копируется всякий раз, когда кто-либо из них нажимает, и выталкивание не приводит к разрыву ссылок в структуре.

Так, когда вещи удаляются? В конечном итоге мы должны вернуть ресурсы, иначе нашей программе может не хватить памяти. Если элемент стека вытолкнут, и ни одна часть программы больше не содержит ссылку на него, со временем он будет возвращен сборщиком мусора. Действительно, сборка мусора является важной функцией для функционального программирования на любом языке.

Минусы клетки, CAR и CDR.

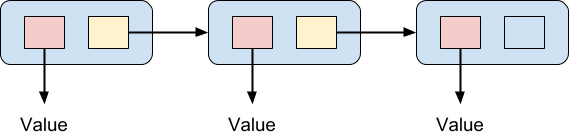
Эта структура стека может показаться вам знакомой. Если это так, это не зря. Эта структура известна как связанный список, и это основополагающая структура данных в информатике. Обычно связанные списки представлены диаграммой примерно так:

Список представляет собой цепочку элементов, и каждый элемент содержит пару указателей. Один из двух указателей указывает на значение. Другой указывает на следующий элемент в цепочке, за исключением последнего элемента в цепочке, который не указывает на другой элемент. Таким образом, цепочка ценностей может быть связана вместе. Одним из преимуществ, обычно упоминаемых для такого рода структуры данных в императивном программировании, является то, что очень просто вставить значение в середину списка: все, что вам нужно сделать, это создать новый элемент, связать его со следующим элементом, и повторно укажите предыдущий элемент в списке на новый элемент. Элементы связанного списка не должны быть непрерывными в памяти и не должны храниться в порядке, в отличие от массива. Массив потребует перестановки всех элементов после вставленного элемента, чтобы освободить место для него, что может быть очень дорогой операцией. С другой стороны, связанные списки работают плохо для произвольного доступа, который является операцией O (n). Это связано с тем, что для поиска n-го элемента вы должны пройти предыдущие (n — 1) элементы, в отличие от массива, где вы можете получить доступ к любому элементу за постоянное время O (1).

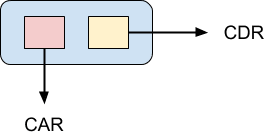
Связанные списки являются важной структурой данных в функциональном программировании. Язык программирования Lisp буквально построен из них. В Лиспе единственный элемент связанного списка называется cons-ячейкой :

Указатель CAR указывает на значение cons-ячейки, а указатель CDR указывает на следующий элемент в списке. CAR и CDR — это архаичные термины, которые больше не используются, но я упоминаю их для исторического интереса, и, возможно, вы можете столкнуться с ними. Язык программирования Lisp был впервые реализован на мэйнфрейме IBM 704, и разработчикам было удобно хранить ячейку cons в машинном слове. Указатель на значение ячейки был сохранен в части «адрес» слова, а указатель на следующую ячейку был сохранен в части «декремент». Это было удобно, потому что на машине были инструкции, которые можно было использовать для прямого доступа к обоим этим значениям, когда ячейка была загружена в регистр. Следовательно, содержимое адресной части регистра и содержимое декрементной части регистра или CAR и CDR для краткости.

Эта номенклатура превратила его в язык; Лисп использовал car в качестве ключевого слова для возврата первого элемента списка и cdr для возврата остальной части списка. В настоящее время Clojure использует first и rest вместо них, что гораздо прозрачнее: вряд ли уместно называть основные языковые операции в честь архитектуры компьютера 1950-х годов. Другие языки могут называть их головой и хвостом .

Создание новой cons-ячейки называется consing, и поэтому оно означает создание списка, добавляя элемент в начале другого списка:

Как мы видели в примере со стеком, добавление элемента в список не изменяет список для любой другой части программы, которая все еще использует его.

Бинарные деревья.

Это все хорошо, но что если мы хотим вставить значение в список или добавить его в конец? В этом случае дублирование необходимо; нам нужно будет продублировать все элементы до той точки списка, в которую будет вставлен новый элемент. В худшем случае — добавление элемента в конец — мы будем вынуждены дублировать весь список.

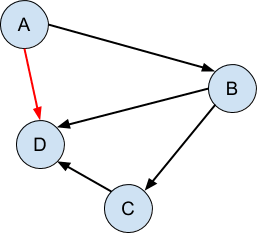
Другой подход заключается в использовании двоичного дерева вместо связанного списка. Это упорядоченная структура данных, в которой каждый элемент имеет ноль, один или два указателя на другие элементы в структуре: один указывает на элемент, значение которого считается ниже, чем текущий элемент, а другой указывает на элемент, значение которого считается больше, при любом сравнении, подходящем для типа данных, хранящихся в дереве:

Бинарное дерево можно искать значительно эффективнее, чем связанный список, но его необходимо сбалансировать для достижения оптимальной производительности. Чтобы быть оптимальным, верхний элемент дерева должен быть медианой всех значений в дереве, и то же самое должно быть верно для верхних элементов всех поддеревьев. В худшем случае, когда двоичное дерево становится полностью перекошенным с обеих сторон, оно становится неотличимым от связанного списка.

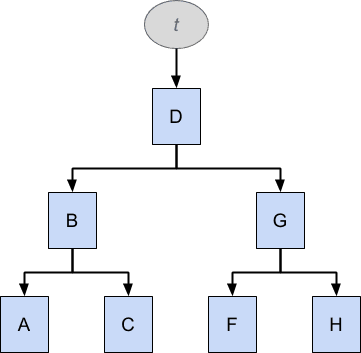
Структура t выше содержит дерево элементов, которые расположены в алфавитном порядке: A, B, C, D, F, G, H. Обратите внимание, что E отсутствует. Следуя стрелкам вниз, элементы слева имеют более низкое значение, чем элементы справа, поэтому вы можете легко перемещаться по дереву, чтобы найти значение, сравнивая значение с каждым элементом по очереди и следуя по дереву вниз + влево или вниз + вправо соответственно , Поэтому такие структуры данных хороши для поиска, а обобщенный вариант, называемый B-деревом , обычно используется для индексации таблиц базы данных.

Теперь давайте представим, что мы хотим вставить отсутствующее значение E в это дерево, которое может выглядеть в коде так:

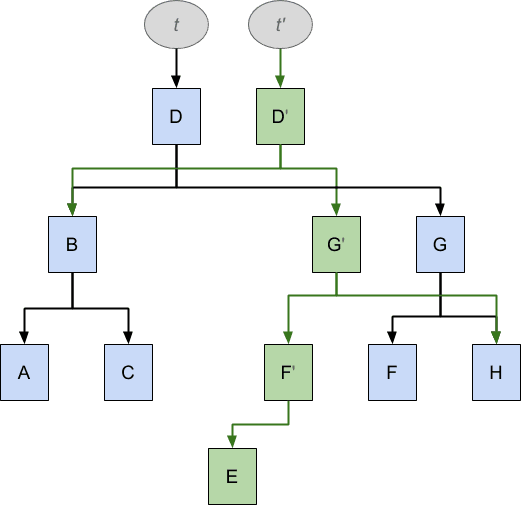
Как и прежде, мы хотим, чтобы эта операция вставки оставляла исходное дерево t без изменений, и в то же время мы хотели бы повторно использовать как можно больше t , чтобы минимизировать дублирование. Результат выглядит так:

Чтобы добиться вставки E, необходимо было дублировать D, G, F, в то время как A, B, C совместно используются двумя структурами данных, но в результате после стрелок из t исходная структура данных остается неизменной, следуя стрелкам из t ‘, мы видим структуру данных, которая теперь также содержит E в правильном положении.

Одно направление.

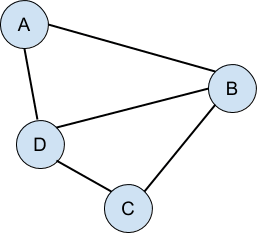
Связанный список и двоичное дерево имеют одну важную общую черту: оба являются примерами направленных ациклических графов . Если вы не слышали этот термин раньше, не расстраивайтесь, потому что это очень просто. Граф — это набор вещей (узлов, точек, вершин и т. Д.), Которые имеют связи между ними:

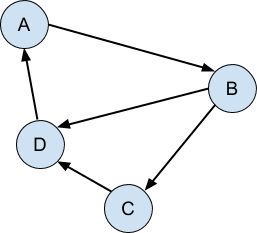
График направлен, когда соединения идут только в одну сторону:

Наконец, граф является ациклическим, когда нет циклов, то есть невозможно проследить за графиком из любой точки и вернуться обратно в ту же самую точку:

Именно направленная ациклическая природа этих структур — то, что за связями можно следовать только в одном направлении и никогда не замыкаться на себя, — позволяет нам «прикрепить» дополнительную структуру, чтобы создать видимость модификации или копирования, в то время как оставляя незатронутыми любые части программы, которые все еще смотрят на оригинальную версию структуры.

Не паникуйте!

Я надеюсь, что мои объяснения здесь имеют какой-то смысл, но если нет, не беспокойтесь слишком сильно. Нет необходимости реализовывать структуры данных, подобные этим, когда вы занимаетесь функциональным программированием — функциональные и гибридно-функциональные языки имеют встроенные неизменяемые структуры данных, которые работают просто отлично, вероятно, лучше, чем все, что большинство из нас могли бы написать.

Причина, по которой я включил этот раздел в сериал, отчасти технический интерес — мне нравится знать, как все это работает — и отчасти, чтобы рассеять опасения по поводу эффективности. Неизменяемые структуры данных не означают создание оптовых копий целых структур каждый раз, когда необходимо что-то изменить; Существуют гораздо более эффективные методы для этого.

В следующий раз.

На этом мы завершаем наше знакомство с увлекательной темой функционального программирования. Я надеюсь, что это было полезно. В следующей статье мы закончим с некоторыми заключительными мыслями. Мы обсудим декларативную природу функционального стиля и то, могут ли функциональные и объектно-ориентированные стили программирования жить вместе. Мы кратко рассмотрим одно из преимуществ функционального программирования, которое я не особо затронул в этой серии — простота параллелизма — и рассмотрим разницу между функциональным стилем и проблемами эффективности.

Вся серия:

1. Вступление
2. Первые шаги
3. Первоклассные функции I: лямбда-функции и карта
4. Первоклассные функции II: фильтрация, уменьшение и многое другое
5. Функции высшего порядка I: Композиция функций и монады
6. Функции высшего порядка II: карри
7. Ленивая оценка
8. Постоянные структуры данных