Функциональный стиль — часть 2

Первые шаги.

В предыдущей статье мы ввели функциональное программирование из первых принципов. Это было много словоблудия и никакой практики. Идея программирования без побочных эффектов все хорошо, но мы должны знать, как на самом деле это сделать. Итак, давайте исследуем это, посмотрев на некоторый код. Римские цифры ката — это хорошее упражнение, которое мы можем использовать для иллюстрации этих идей.

Римские цифры.

Вкратце, римские цифры представляют собой систему счисления, которая представляет числа с использованием букв латинского алфавита: число один представлено I , пять — V , десять — X , пятьдесят — L , сто — C , пятьсот — D , и тысяча М. Правила таковы:

1. Когда цифры появляются слева от цифр с меньшим или равным значением, значения добавляются, поэтому II — это два, III — три, а VI — шесть.
2. Когда цифра с более низким значением появляется слева от цифры с более высоким значением, нижнее значение вычитается из более высокого значения. Поэтому IV — четыре, IX — девять, а XL — сорок.

Оба правила применяются одновременно в любом заданном количестве, поэтому:

• XIV составляет 14, то есть 10 + (5 — 1)
• LIX составляет 59, то есть 50 + (10 — 1)
• CXL составляет 140, то есть 100 + (50 — 10).

Вооружившись этими знаниями, мы можем написать в Groovy спецификацию для преобразования индуистских арабских чисел в римские:

Ключом к решению этого упражнения является устранение особых случаев, рассматривая вычитающие пары как самостоятельные цифры, то есть CM — девятьсот, CD — четыреста, XC — девяносто, XL — сорок, IX — девять, IV — четыре , Когда вы делаете это, проблема становится чисто аддитивной. В итоге вы получите набор символов, которые могут быть собраны в действительную римскую цифру и таким образом суммированы равными любому натуральному числу:

Существует несколько способов реализации этого ката, но, вероятно, наиболее очевидным является использование символов в порядке убывания значения. Хотя текущее значение символа меньше или равно числу, несколько раз добавляйте символ к выводу и вычитайте значение из числа; в противном случае перейдите к следующему символу. Продолжайте повторять, пока не вычтите число до нуля. Строка символов, которые вы добавили вместе, является вашим результатом:

Этот код в порядке, но работает ли он? Согласно первому определению, которое я дал в первой части, это:

В функциональном коде выходное значение функции зависит только от аргументов, которые передаются функции, поэтому при вызове функции f дважды с одним и тем же значением для аргумента x каждый раз получается один и тот же результат f (x).

Это, безусловно, верно для этой функции: при определенных входных данных она всегда возвращает одно и то же значение. Он не изменяет никакое состояние вне своей собственной области, и при этом это не зависит от любого состояния вне его собственной области, которое может быть изменено любым другим потоком. (Вот почему я реализовал метод для создания карты символов по запросу). Он соответствует критериям для чистой функции.

Но написано ли это в функциональном стиле? Не за что. Может не быть глобального состояния, но есть внутреннее состояние, и оно, безусловно, изменяется. Он объединяет строки для получения результата и многократно вычитает из входного числа. Он даже изменяет свой параметр, против которого будут возражать многие программисты, даже если они в других отношениях не чувствуют себя мутирующими. В целом, алгоритм крайне важен по своей природе:

• Создайте пустую строку.
• Делайте это, пока число больше или равно значению символа.
• Добавьте цифру к строке.
• Вычтите из числа.

Так как же нам переписать этот код, чтобы он стал менее обязательным? В частности, как мы реализуем итерацию, не переназначая ничего? В нашем цикле необходимо отслеживать три вещи:

• Счетчик итераций (хорошо, цикл for обрабатывает это для нас неявно, поэтому мы можем притвориться, что его там нет).
• Строка выходных чисел.
• Результат вычитания.

Итерировать — это человек; повторять, божественно.

Ответ — мы используем рекурсию. Давайте разберем предмет с более простым примером. Эта функция отсчитывает от заданного числа:

Состояние, изменяемое в этой функции, является счетчиком цикла i . Мы можем избежать его изменения, заставив функцию вызывать себя:

Он ведет себя точно так же, но теперь ничего не переназначается. Функциональное совершенство здесь сопряжено с двумя затратами: во-первых, небольшое снижение читабельности. Вторая стоимость мы придем в ближайшее время.

Чтобы переписать нашу функцию римских цифр в рекурсивный алгоритм, будет проще, если сначала мы сведем вложенные циклы в один цикл, например так:

Да, я согласен, что это не улучшение по сравнению с оригиналом, но теперь мы можем легче реорганизовать функцию для использования рекурсии:

К сожалению, нам пришлось перегружать метод convert , но мы пока не будем convert на это внимание. Перегрузка принимает остаток, числовой индекс и строку, которая накапливает результат. Если остаток равен нулю, то накопленная строка уже содержит результат, поэтому мы его возвращаем. В противном случае мы получаем символ и значение по данному числовому индексу. Если значение меньше или равно остатку, добавьте символ к результату, вычтите значение из остатка и рекурсивно. Если значение больше, чем остаток, увеличьте числовой индекс и введите значение.

Теперь у нас есть алгоритм, который не присваивает значение чему-либо. Это также намного менее важно в природе. Единственное утверждение, оставленное в коде, является присваиванием

и даже это может быть учтено, если мы захотим.

Но так ли это лучше? Лично я бы так не сказал: оригинальная версия была короче, понятнее и не нуждалась в перегрузке для функции преобразования. Давайте проведем эксперимент и посмотрим, как это выглядит на функциональном языке. Используя тестовую библиотеку Брайана Марика Midje, мы можем написать ряд фактов в Clojure:

Пока не сильно отличается. Эквивалентная реализация в Clojure выглядит следующим образом:

Если вы не знакомы с Lisp, то это может выглядеть немного странно, но синтаксис Lisp на самом деле нелепо прост. В большинстве языков вызов функции f с передачей аргументов x и y выглядит следующим образом: f(x, y) . Чтобы превратить его в Лисп, просто удалите запятые и переместите открытую часть влево от имени функции: (fxy) . Это почти все, что Лисп уже выучил. Как и в версии Groovy, код Clojure перегружает функцию преобразования, принимая либо один параметр [number] либо три параметра [remainder numeral-index roman] . Значения параметров такие же, как в Groovy.

Форма if в Clojure является выражением, идентичным по своему действию тернарному оператору в языках стиля C:

Выражение cond оценивается как значение, и любое значение в Clojure можно рассматривать как истинное или ложное; nil и false — ложь, а все остальное — правда. Этот стиль программирования с выражениями, а не с утверждениями, приводит к созданию близких скобок в конце строк, что многие люди считают нежелательным в отношении Lisp. Haskell избегает этой проблемы, обходясь без скобок. У Clojure есть пара макросов, которые тоже улучшают проблему, но мы вернемся к этому позже.

Единственная часть этого кода Clojure, которая немного волшебна, — эта часть:

Смысл (nth numerals numeral-index) должен быть очевиден: он дает вам n-й элемент из вектора numeral-index где n равно numeral-index . Это будет вектор из двух элементов, например ["M" 1000] . Мы используем функцию Clojure, называемую деструктуризацией, чтобы назначить symbol первому элементу в векторе («M») и value второму (1000).

Помимо личного вкуса, между двумя версиями есть немного. Основное отличие состоит в том, что функциональные языки неумолимо приводят вас к рекурсии с помощью выбора дизайна, сделанного на самом языке. В Groovy у вас есть возможность использовать цикл. В императивном языке вы всегда выбираете циклическую рекурсию, если итерационный алгоритм возможен, потому что он работает лучше. Это вторая цена, о которой я упоминал ранее, и это важная вещь.

Ликвидация хвоста.

Всякий раз, когда вы пишете рекурсивную программу, вы должны заранее знать, насколько глубокой будет эта рекурсия, чтобы не разбить стек. Программа, которая переходит к подпрограмме, помещает адрес возврата в стек, который должен быть выдан после завершения подпрограммы. Если эта подпрограмма вызывает другую подпрограмму, то она помещает свой собственный обратный адрес сверху. В стеке хранятся все адреса возврата в правильном порядке, поэтому программа всегда может вернуть управление туда, откуда оно пришло. Очевидно, что чем больше глубина вложенности в ваших подпрограммах, тем больше требуется стека. В нерекурсивном коде это не проблема: вы никогда не достигнете глубины вложенности, необходимой для нехватки памяти. Но рекурсивные подпрограммы называют себя! В функциональном программировании рекурсия является методом выбора для выполнения итерации, но это делает перспективу создания стека очень реалистичной.

Этой проблемы можно избежать. Ключ в том, чтобы позиционировать вызовы подпрограмм так, чтобы они находились в хвостовой позиции . Это означает, что больше нет инструкций между возвратом управления из подпрограммы и концом подпрограммы, которая ее вызвала. Другими словами, когда подпрограмма A вызывает подпрограмму B из хвостовой позиции, управление возвращается из B только для немедленного возврата к вызывающей стороне A. Давайте проиллюстрируем это некоторым кодом. Рассмотрим глупый пример обратного отсчета из ранее:

Рекурсивный вызов countDown находится в хвостовой позиции, потому что когда он возвращается, в вызывающей функции больше нечего делать. Итак, давайте рассмотрим рекурсивный вызов, который не находится в хвостовой позиции:

Рекурсивный вызов factorial не находится в хвостовой позиции, потому что его результат должен быть умножен на n чтобы вычислить возвращаемое значение для вызова внешней функции. Но почему это важно? Это важно, потому что, как заметил Гай Л. Стил в газете для ACM в 1977 году, вызов подпрограммы в хвостовой позиции может быть заменен на goto . В отличие от вызова подпрограммы, goto не ожидает возврата элемента управления к вызывающей подпрограмме, поэтому в стек вызовов не передается адрес возврата.

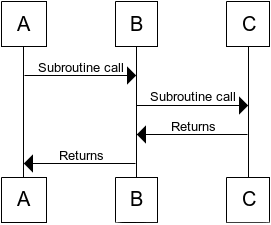
Мы можем показать наблюдение Стила на диаграмме, показывающей два вложенных вызова подпрограммы:

Здесь подпрограмма A вызывает подпрограмму B, а затем B вызывает подпрограмму C. По завершении C извлекает адрес возврата из стека вызовов, чтобы вернуться к B, а B извлекает предыдущий адрес возврата, чтобы вернуться к A.

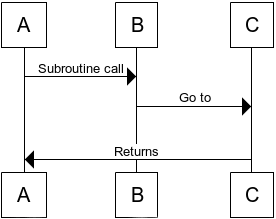
Но, как заметил Стил, если вызов C находится в хвостовой позиции, то B может также перейти непосредственно к C, оставив свой собственный адрес возврата поверх стека вызовов, потому что C вытолкнет этот адрес и вернется непосредственно к A. это то, что мы хотели случиться в любом случае. Это называется устранением хвостовых вызовов, и преимущество имеет два аспекта: во-первых, мы избежали одной ненужной инструкции перехода и, что гораздо важнее, избежали увеличения стека вызовов.

Если вы удалите хвостовые вызовы таким способом в рекурсивном алгоритме, вы получите подпрограмму, которая многократно переходит к своей точке входа, пока не будет достигнуто условие завершения. С точки зрения машины это ничем не отличается от обычного цикла!

Ах, но есть подвох. Вы должны программировать на языке, который выполняет этот вид оптимизации. .NET время выполнения, при определенных обстоятельствах. JVM не делает. Поэтому функциональные языки, работающие на JVM, должны обеспечивать обходные пути. Scala будет оптимизировать хвостовые рекурсивные функции в циклы, когда это возможно, и вы можете убедиться в этом, @tailrec функции, для которых вы хотите получить эту обработку, с помощью @tailrec . (Компилятор выдаст ошибку, если аннотированная функция @tailrec на самом деле не является хвостовой рекурсией). Clojure предоставляет форму loop..recur которая также переписывает ваш код в цикл, давая вам «ощущение» рекурсии:

Это также позволяет нам избавиться от перегрузки, которая существовала только для поддержки рекурсии. Если мы вернемся к исходной версии этого кода на Groovy, я думаю, что функциональный код не более сложен, чем оригинальный, и несколько более элегантен:

Ссылочная прозрачность.

Прежде чем мы закончим, вернемся к этой версии кода римских цифр в Groovy:

Мы можем вычислить римское представление 14, numeralIndex значения непосредственно для remainder аргументов, numeralIndex и roman аргументов. Я немного обманул, установив индекс аргумента на 8; Я сделал это, чтобы пропустить прямые цифры с более высоким значением. В противном случае это упражнение, которое уже довольно затянуто, станет значительно длиннее:

Существует свойство чистых функций, как и у метода convert(int, int, String) , что мы можем копировать реализацию прямо по ее вызову, например так:

Это свойство чистых функций называется ссылочной прозрачностью . Я также скопировал литеральные значения по numeral.value и numeral.symbol потому что они просматривались из массива по значению литерального индекса, поэтому это упрощение было возможно. Теперь некоторые пути через этот код гарантированно не будут приняты: 14 явно не равно 0 и явно больше 10. Таким образом, мы можем вручную удалить все ветви, которые гарантированно не будут приняты, и код сводится к этому:

Теперь мы можем заменить вызов метода convert снова:

Еще раз мы можем удалить все ветви, которые гарантированно не будут заняты, и на этот раз это сводится к следующему:

Давайте сделаем замену снова. На этот раз мы заменим numeral.value на 9 и numeral.symbol на «IX»:

Опять же, мы можем увидеть своими глазами, какие ветви гарантированно будут заняты, поэтому мы можем сократить код до следующего:

и снова замените вызов метода, на этот раз заменив numeral.value на 5 и numeral.symbol на ‘V’:

Еще раз мы удаляем все ветки, которые гарантированно не будут приняты, и получаем:

Мы заменим вызов метода еще раз, заменив 4 для numeral.value на и «IV» для numeral.symbol :

И на этот раз устранение не взятых веток приводит к такому

В самый последний раз мы копируем вызов метода:

и поскольку (((14 - 10) - 4) == 0) верно, мы видим, что конечный результат:

что дает XIV , четырнадцать.

В предыдущей статье я говорил, что программирование без переопределения значения символа может привести к взрыву количества символов. По крайней мере, кажется, что так и должно быть. Но этот процесс многократной замены вызова функции его реализацией, хотя и очень трудоемкий, не привел к увеличению количества символов, используемых в программе.

Вы рекомендуете нам программировать таким образом?

Не за что. Когда я программирую на императивном языке, я все еще использую итерацию над рекурсией. Если вы помните в части 1, я сказал, что в каждом императивном языке есть определенное место для FP. Это конечно не так. Эта статья ни в коем случае не является убийственным аргументом для функционального программирования, фактически сама по себе она не подходит для FP. Вместо этого моя цель — объяснить основы и продемонстрировать, что программирование без изменения состояния действительно возможно. Я постараюсь объяснить, почему это желательно позже.

В следующий раз:

Если бы это было все, что было с функциональным программированием, я бы простил вас за то, что вы думаете, что это не стоит шумихи. К счастью, это далеко не все. Мы видели некоторое функциональное программирование здесь, но не то, что я бы назвал функциональным стилем. Когда вы программируете в функциональном стиле, вам очень редко нужно писать циклы любого рода. Цикл — это средство для достижения цели, а не самоцель. Функциональный стиль позволяет программировать больше с точки зрения желаемых целей и меньше беспокоиться о средствах их достижения. В следующей статье я начну раскрывать эту тему. Мы познакомим вас с первоклассными функциями и лямбда-выражениями, а также с тем, как их использование часто позволяет вообще избежать необходимости писать явные циклы.