Произвольная точность и большие числа в PHP

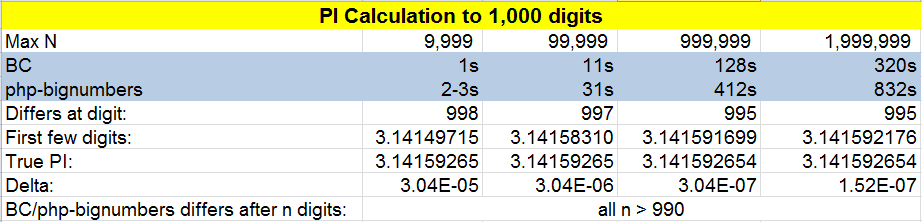
Я проверил производительность (как с точки зрения скорости, так и точности) с разными значениями n

Откровенно говоря, этот результат действительно разочаровывает меня. При максимальном значении N, равном 2 миллионам, мы можем достичь точности только с точностью до шестого знака после запятой (3.141592) по сравнению с реальным PI. Но это связано со скоростью сходимости самого алгоритма.

Оба метода (BC и php-bignumbers) демонстрируют высокий уровень идентичности результатов: для 1000+ цифр они отличаются только после 990-й цифры. Это эквивалентно разнице 10E-990, которой достаточно для того, чтобы мы с одинаковым доверием относились к идентичности их выходов. Другими словами, при одинаковом алгоритме эти две библиотеки выдают «одинаковый» результат.

Однако скорости имеют огромный разрыв. Грубо говоря, BC занимает только 1/3 времени от числа php-номеров. Я полагаю, что это потому, что lib php-bignumbers тратит много времени на обработку, связанную с OO.

Обе библиотеки (а также GMP) внутренне используют строки для хранения чисел произвольной точности, формируя эту строку в указанные нами цифры. Манипуляции со строками также замедляют производительность. Также существует тот факт, что BC написан и выполняется на низком уровне — в C — тогда как bignumbers — это просто высокоуровневая PHP-библиотека.

Если мы снизим точность до 100 цифр, время будет значительно сокращено. Когда n = 999,999, 15 и 85 пройдут для BC и php-bignumbers, соответственно, и точность вывода все еще сохраняется. Результаты двух библиотек будут отличаться от 95-й цифры из 100+. Нам все еще удобно говорить, что они идентичны.

Таким образом, предложение на данном этапе BC все еще рекомендуется. Это обеспечивает ту же точность, но намного быстрее. Чтобы сэкономить время при выполнении вычислений произвольной точности, настоятельно рекомендуется установить меньшую шкалу точности. Время будет примерно 1/10, если масштаб 1/10 (1000 цифр стоят 128 с, а 100 цифр — 15 с для BC. Для php-номеров это всего 1/5).

Просто чтобы довести наше обсуждение до крайности, я вставил несколько строк кода, чтобы посмотреть, каков будет результат, если мы не будем полагаться на какие-либо библиотеки и просто используем встроенные плавающие числа.

Результат потрясающий. Когда n установлено в 999 999, встроенное плавающее число дает результат 3.1415916986586, почти идентичный тому, что мы можем получить из BC (3.1415916986595…). Но угадайте что? Это заканчивается почти мгновенно!

Таким образом, мой вывод таков: если мы не заботимся о цифрах, начиная с 10-й цифры и выше, нам, вероятно, вообще не следует использовать какие-либо произвольные библиотеки.

 <?php

$letter = 'A';

$m = ord($letter); // ASCII code of letter 'A'
$d = 2753;

$e = 17;
$n = 3233;

echo "Encryption / Decryption using BC:\n";
$c = bcmod(bcpow($m, $e, 40), $n);
$res = bcmod(bcpow($c, $d, 40), $n);

echo "Original data: $letter\n";
echo "Encrypted data: $c\n";
echo "Decryption:\n";
echo "Input: $c\n";
echo "Decrypted: $res\n";
echo "The letter is: ".chr($res)."\n";

echo "=========================\n";
echo "Encryption / Decryption using GMP:\n";
$c = gmp_powm($m, $e, $n);
$res = gmp_powm($c, $d, $n);

echo "Original data: $letter\n";
echo "Encrypted data:".gmp_strval($c)." \n";
echo "Decryption:\n";
echo "Input: ".gmp_strval($c)."\n";
echo "Decrypted: ".gmp_strval($res)."\n";
echo "The letter is: ".chr(gmp_strval($res))."\n";