Как создать векторную графику на iOS

Вступление

Графические ресурсы в цифровом мире бывают двух основных типов, растровые и векторные. Растровые изображения представляют собой прямоугольный массив интенсивностей пикселей. Векторная графика, с другой стороны, является математическим представлением форм.

Хотя существуют ситуации, когда растровые изображения незаменимы (например, фотографии), в других сценариях векторная графика способна заменить. Векторная графика делает задачу создания графических ресурсов для нескольких разрешений экрана тривиальной. На момент написания этой статьи на платформе iOS было как минимум полдюжины разрешений экрана.

Одна из лучших особенностей векторной графики заключается в том, что она может быть отрисована в любом разрешении, оставаясь абсолютно четкой и плавной. Вот почему шрифты PostScript и TrueType выглядят четкими при любом увеличении. Поскольку дисплеи смартфонов и компьютеров имеют растровую природу, в конечном счете, векторное изображение необходимо отображать на дисплее как растровое изображение с соответствующим разрешением. Об этом обычно заботится низкоуровневая графическая библиотека, и программисту не нужно беспокоиться об этом.

1. Когда использовать векторную графику?

Давайте посмотрим на некоторые сценарии, где вы должны рассмотреть возможность использования векторной графики.

Значки приложений и меню, элементы интерфейса пользователя

Несколько лет назад Apple отказалась от скеоморфизма в пользовательском интерфейсе своих приложений и самой iOS в пользу смелых и геометрически точных дизайнов. Взгляните, например, на значки приложений «Камера» или «Фото».

Скорее всего, они были разработаны с использованием инструментов векторной графики. Разработчики должны были последовать их примеру, и большинство популярных (неигровых) приложений претерпели полную метаморфозу, чтобы соответствовать этой парадигме дизайна.

Игры

Игры с простой графикой (например, астероиды ) или геометрическими темами (вспоминаются Super Hexagon и Geometry Jump) могут отображать свои спрайты из векторов. То же самое относится к играм, которые имеют процедурно сгенерированные уровни.

Картинки

Изображения, в которые вы хотите добавить небольшое количество случайности, чтобы получить несколько версий одной базовой формы.

2. Кривые Безье

Что такое кривые Безье? Не углубляясь в математическую теорию, давайте просто поговорим об особенностях, которые полезны для разработчиков.

Степени свободы

Кривые Безье характеризуются тем, сколько степеней свободы они имеют. Чем выше эта степень, тем больше вариаций может включать кривая (но и тем сложнее она математически).

Степень Безье — отрезки прямой. Степени двух кривых называются квадратическими. Мы сфокусируемся на трех кривых (кубах), потому что они предлагают хороший компромисс между гибкостью и сложностью.

Кубические Безье могут представлять не только простые гладкие кривые, но также петли и вершины. Несколько кубических сегментов Безье могут быть соединены друг с другом, чтобы сформировать более сложные формы.

Кубический безье

Кубический Безье определяется двумя конечными точками и двумя дополнительными контрольными точками, которые определяют его форму. Как правило, степень Безье имеет (n-1) контрольных точек, не считая конечных точек.

Привлекательная особенность кубического Безье в том, что эти точки имеют значительную визуальную интерпретацию. Линия, соединяющая конечную точку с соседней контрольной точкой, действует как касательная к кривой в конечной точке. Этот факт полезен для проектирования фигур. Мы будем использовать это свойство позже в этом уроке.

Геометрические преобразования

Из-за математической природы этих кривых вы можете легко применять к ним геометрические преобразования, такие как масштабирование, вращение и перемещение, без потери точности.

На следующем рисунке показана выборка различных форм, которые может принять один кубический Безье. Обратите внимание, как сегменты зеленой линии действуют как касательные к кривой.

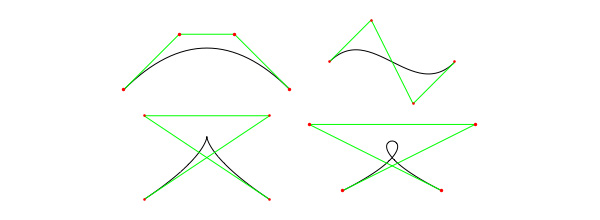
3. Базовая графика и класс UIBezierPath

В iOS и OS X векторная графика реализована с использованием библиотеки Core Graphics на основе C. Поверх этого построен UIKit / Cocoa, который добавляет фанеру ориентации объекта. Рабочая лошадка — класс UIBezierPath ( NSBezierPath в OS X), реализация математической кривой Безье.

Класс UIBezierPath поддерживает кривые Безье степени один (прямые отрезки), два (четырехугольные кривые) и три (кубические кривые).

Программно объект UIBezierPath может быть построен по частям путем добавления к нему новых компонентов (подпутей). Для этого объект UIBezierPath отслеживает свойство UIBezierPath . Каждый раз, когда вы добавляете новый сегмент пути, последняя точка добавленного сегмента становится текущей точкой. Любой дополнительный рисунок, который вы делаете, обычно начинается с этого момента. Вы можете явно переместить эту точку в нужное место.

Класс имеет удобные методы для создания часто используемых фигур, таких как дуги и круги, (закругленные) прямоугольники и т. Д. Внутренне эти формы были построены путем соединения нескольких подпутей.

Общая траектория может быть открытой или закрытой. Он может даже быть самопересекающимся или иметь несколько закрытых компонентов.

4. Начало работы

Это руководство предназначено для того, чтобы дать представление о генерации векторной графики. Но даже если вы опытный разработчик, который раньше не использовал Core Graphics или UIBezierPath , вы должны быть в состоянии это сделать. Если вы новичок в этом, я рекомендую UIBezierPath ссылку на класс UIBezierPath (и базовые функции Core Graphics), если вы еще не знакомы с ним. Мы можем использовать только ограниченное количество функций API в одном руководстве.

Хватит разговоров. Давайте начнем кодировать. В оставшейся части этого урока я представлю два сценария, в которых векторная графика является идеальным инструментом для использования.

Запустите Xcode, создайте новую игровую площадку и установите платформу на iOS. Кстати, игровые площадки XCode — еще одна причина, почему работа с векторной графикой теперь забавна. Вы можете настроить свой код и получить мгновенную визуальную обратную связь. Обратите внимание, что вы должны использовать последнюю стабильную версию Xcode, которая на момент написания этой статьи составляла 7.2.

Сценарий 1: создание форм облаков

Мы хотели бы создать изображения облаков, которые придерживаются основной формы облаков и имеют некоторую случайность, чтобы каждое облако выглядело по-разному. Базовый дизайн, на котором я остановился, представляет собой сложную форму, определяемую несколькими кругами случайных радиусов, центрированных вдоль эллиптической траектории случайных размеров (в соответствующих диапазонах).

Чтобы уточнить, вот как выглядит весь объект, если мы обводим векторную дорожку вместо ее заполнения.

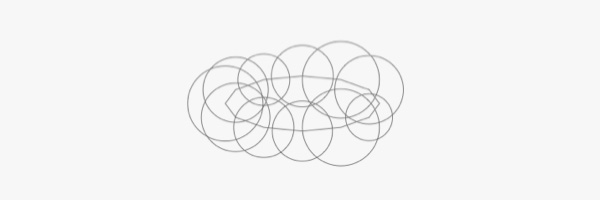
Если ваша геометрия немного ржавая, то это изображение из Википедии показывает, как выглядит эллипс.

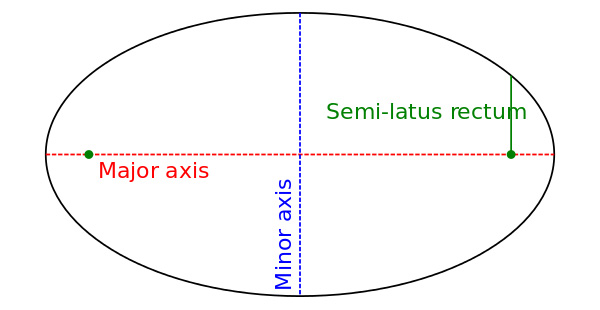
Некоторые служебные функции

Давайте начнем с написания пары вспомогательных функций.

« `импорт JavaScript из UIKit

func randomInt (нижний нижний: Int, верхний: Int) -> Int {assert (нижний <верхний) возвращает нижний + Int (arc4random_uniform (UInt32 (верхний — нижний))))}

функциональный круг (в центре: CGPoint, радиус: CGFloat) -> UIBezierPath {return UIBezierPath (arcCenter: центр, радиус: радиус, startAngle: 0, endAngle: CGFloat (2 * M_PI), по часовой стрелке: true)} « `

Функция random(lower:upper:) использует встроенную arc4random_uniform() для генерации случайных чисел в lower диапазоне и (upper-1) . Функция circle(at:center:) генерирует путь Безье, представляющий круг с данным center и radius .

Генерация точек и путей

Давайте теперь сосредоточимся на создании точек вдоль эллиптического пути. Эллипс с центром в начале системы координат, оси которого выровнены вдоль осей координат, имеет особенно простую математическую форму, которая выглядит следующим образом.

P(r, θ) = (a cos(θ), b sin(θ))

Мы назначаем случайные значения для длины его большой и малой оси, чтобы форма выглядела как облако, вытянутое по горизонтали больше, чем по вертикали.

Мы используем функцию stride() для генерации равномерно распределенных углов вокруг круга, а затем используем map() для генерации равномерно распределенных точек на эллипсе, используя приведенное выше математическое выражение.

« `javascript let a = Double (randomInt (нижний: 70, верхний: 100)) let b = Double (randomInt (нижний: 10, верхний: 35)) let ndiv = 12 как Double

  let points = (0.0) .stride (до: 1.0, by: 1 / ndiv) .map {CGPoint (x: a * cos (2 * M_PI * $ 0), y: b * sin (2 * M_PI * $ 0)) } `` `

Мы генерируем центральную «массу» облака, соединяя точки вдоль эллиптического пути. Если мы этого не сделаем, мы получим большую пустоту в центре.

« `javascript let path = UIBezierPath () path.moveToPoint (points [0])

для точки в точках [1 .. <points.count] {path.addLineToPoint (point)}

path.closePath () « `

Обратите внимание, что точный путь не имеет значения, потому что мы будем заполнять путь, а не гладить его. Это означает, что он не будет отличим от кругов.

Чтобы создать круги, мы сначала эвристически выбираем диапазон для случайных радиусов окружности. Тот факт, что мы развиваем это на детской площадке, помог мне играть со значениями, пока я не получил результат, которым я был доволен.

« `javascript let minRadius = (Int) (M_PI * a / ndiv) let maxRadius = minRadius + 25

для точки в точках [0 .. <points.count] {let randomRadius = CGFloat (randomInt (нижний: minRadius, верхний: maxRadius)) let circ = окружность (в: point, radius: randomRadius) path.appendPath (circ)}

путь « `

Предварительный просмотр результата

Вы можете просмотреть результат, щелкнув значок «глаз» на панели результатов справа, в той же строке, что и оператор «путь».

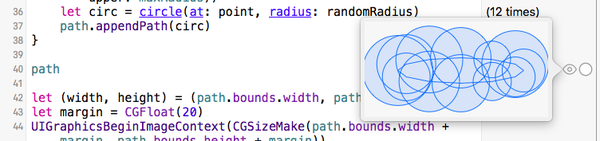
Последние штрихи

Как мы растеризуем это, чтобы получить окончательный результат? Нам нужен так называемый «графический контекст», в котором можно рисовать пути. В нашем случае мы будем рисовать изображение (экземпляр UIImage ). Именно в этот момент вам нужно установить несколько параметров, определяющих, каким будет окончательный путь, например, цвета и ширину обводки. Наконец, вы гладите или заполняете свой путь (или оба). В нашем случае мы хотим, чтобы наши облака были белыми, и мы хотим только заполнить их.

Давайте упакуем этот код в функцию, чтобы мы могли генерировать столько облаков, сколько пожелаем. И пока мы работаем над этим, мы напишем некоторый код, чтобы нарисовать несколько случайных облаков на синем фоне (представляющих небо) и нарисовать все это в режиме реального времени на игровой площадке.

Вот окончательный код:

« `импорт JavaScript UIKit импорт XCPlayground

func generateRandomCloud () -> UIImage {

  func randomInt (нижний нижний: Int, верхний: Int) -> Int {
     утверждать (нижний <верхний)
     вернуть нижний + Int (arc4random_uniform (UInt32 (верхний - нижний)))
 }

 функциональный круг (в центре: CGPoint, радиус: CGFloat) -> UIBezierPath {
     return UIBezierPath (arcCenter: центр, радиус: радиус, startAngle: 0, endAngle: CGFloat (2 * M_PI), по часовой стрелке: true)
 }

 let a = Double (randomInt (нижний: 70, верхний: 100))
 let b = Double (randomInt (нижний: 10, верхний: 35))
 let ndiv = 12 как Double


 let points = (0.0) .stride (до: 1.0, by: 1 / ndiv) .map {CGPoint (x: a * cos (2 * M_PI * $ 0), y: b * sin (2 * M_PI * $ 0)) }

 let path = UIBezierPath ()
 path.moveToPoint (точки [0])
 за точку в точках [1 .. <points.count] {
     path.addLineToPoint (точка)
 }
 path.closePath ()


 let minRadius = (Int) (M_PI * a / ndiv)
 пусть maxRadius = minRadius + 25

 за точку в точках [1 .. <points.count] {
     let randomRadius = CGFloat (randomInt (нижний: minRadius, верхний: maxRadius))
     let circ = circle (at: point, radius: randomRadius)
     path.appendPath (CIRC)
 }

 //Обратный путь
 let (width, height) = (path.bounds.width, path.bounds.height)
 let margin = CGFloat (20)
 UIGraphicsBeginImageContext (CGSizeMake (path.bounds.width + margin, path.bounds.height + margin))
 UIColor.whiteColor (). SetFill ()
 path.applyTransform (CGAffineTransformMakeTranslation (ширина / 2 + поле / 2, высота / 2 + поле / 2))
 path.fill ()
 let im = UIGraphicsGetImageFromCurrentImageContext ()
 вернуть им}

Вид класса: UIView {переопределить функцию drawRect (rect: CGRect) {let ctx = UIGraphicsGetCurrentContext () UIColor.blueColor (). setFill () CGContextFillRect (ctx, rect)

  let cloud1 = generateRandomCloud (). CGImage
     let cloud2 = generateRandomCloud (). CGImage
     let cloud3 = generateRandomCloud (). CGImage
     CGContextDrawImage (ctx, CGRect (x: 20, y: 20, ширина: CGImageGetWidth (cloud1), высота: CGImageGetHeight (cloud1)), cloud1)
    
     CGContextDrawImage (ctx, CGRect (x: 300, y: 100, ширина: CGImageGetWidth (cloud2), высота: CGImageGetHeight (cloud2)), cloud2)
    
     CGContextDrawImage (ctx, CGRect (x: 50, y: 200, ширина: CGImageGetWidth (cloud3), высота: CGImageGetHeight (cloud3)), cloud3)
 }}

XCPlaygroundPage.currentPage.liveView = View (frame: CGRectMake (0, 0, 600, 800))

« `

И вот как выглядит окончательный результат:

Silhouttes из облаков выглядят немного размытыми на изображении выше, но это просто артефакт изменения размера. Истинное изображение получается четким.

Чтобы просмотреть его на собственной игровой площадке, убедитесь, что помощник редактора открыт. Выберите Show Assitant Editor в меню View .

Сценарий 2: создание фрагментов головоломки

Кусочки мозаики обычно имеют квадратную «рамку», причем каждый край либо плоский, с закругленным выступом, выступающим наружу, либо прорезью такой же формы, чтобы расселить с помощью язычка из соседнего куска. Вот раздел типичной головоломки.

Размещение вариантов с векторной графикой

Если вы разрабатываете приложение-головоломку, вы бы хотели использовать маску в форме кусочка головоломки, чтобы сегментировать изображение, представляющее головоломку. Вы можете использовать предварительно сгенерированные растровые маски, поставляемые с приложением, но вам нужно будет включить несколько вариантов, чтобы учесть все возможные вариации формы четырех ребер.

С векторной графикой вы можете создать маску для любого вида фигуры на лету. Кроме того, было бы легче приспособить другие варианты, например, если вы хотели прямоугольные или наклонные части (вместо квадратных частей).

Проектирование границы Jigsaw Piece

Как мы на самом деле спроектируем кусок головоломки, то есть как выяснить, как разместить наши контрольные точки, чтобы сгенерировать путь Безье, который выглядит как изогнутая вкладка?

Вспомните полезное свойство касания кубических Безье, о котором я упоминал ранее. Вы можете начать с рисования аппроксимации нужной фигуры, разбив ее на сегменты, оценив, сколько кубических сегментов вам понадобится (зная типы фигур, которые может вместить один кубический сегмент), а затем нарисовав касательные к этим сегментам, чтобы выяснить, где вы можете разместить свои контрольные точки. Вот диаграмма, объясняющая, о чем я говорю.

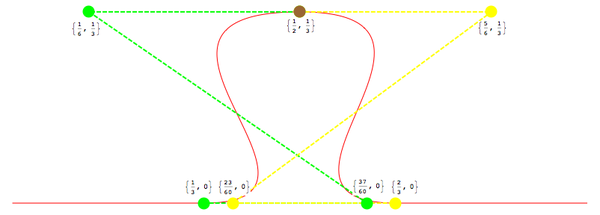
Отношение формы к контрольным точкам кривой Безье

Я определил, что для представления формы вкладки хорошо подойдут четыре сегмента Безье:

• два, представляющие отрезки прямой линии на любом конце формы
• два представляют S-образные сегменты, представляющие выступ в центре

Обратите внимание на зеленые и желтые пунктирные отрезки, которые действуют как касательные к S-образным сегментам, что помогло мне определить, где разместить контрольные точки. Также обратите внимание, что я визуализировал кусок как имеющий длину в одну единицу, поэтому все координаты являются долями одного. Я мог бы легко сделать свою кривую, скажем, длиной в 100 точек (масштабируя контрольные точки в 100 раз). Независимость разрешения векторной графики означает, что это не проблема.

Наконец, я использовал кубические Безье даже для отрезков прямых линий исключительно для удобства, чтобы код мог быть написан более кратко и равномерно.

Я пропустил рисование контрольных точек прямых сегментов на диаграмме, чтобы избежать беспорядка. Конечно, кубический Безье, представляющий линию, просто имеет конечные точки и контрольные точки, лежащие вдоль самой линии.

Тот факт, что вы разрабатываете это на игровой площадке, означает, что вы можете легко перенастроить значения контрольной точки, чтобы найти форму, которая вам нравится, и получить мгновенную обратную связь.

Начиная

Давайте начнем. Вы можете использовать ту же игровую площадку, что и раньше, добавив на нее новую страницу. Выберите New> Playground Page в меню File или создайте новую площадку, если хотите.

Замените любой код на новой странице следующим:

« `импорт JavaScript из UIKit

let outie_coords: [(x: CGFloat, y: CGFloat)] = [(1.0 / 9, 0), (2.0 / 9, 0), (1.0 / 3, 0), (37.0 / 60, 0), (1.0 / 6, 1,0 / 3), (1,0 / 2, 1,0 / 3), (5,0 / 6, 1,0 / 3), (23,0 / 60, 0), (2,0 / 3, 0), (7,0 / 9, 0 ), (8,0 / 9, 0), (1,0, 0)]

let size: CGFloat = 100 let outie_points = outie_coords.map {CGPointApplyAffineTransform (CGPointMake ($ 0.x, $ 0.y), CGAffineTransformMakeScale (размер, размер))}

let path = UIBezierPath () path.moveToPoint (CGPointZero)

для i в 0.stride (через: outie_points.count — 3, через: 3) {path.addCurveToPoint (outie_points [i + 2], controlPoint1: outie_points [i], controlPoint2: outie_points [i + 1])}

путь « `

Генерация всех четырех сторон с использованием геометрических преобразований

Обратите внимание, что мы решили сделать наш путь длиной 100 точек, применив масштабное преобразование к точкам.

Мы видим следующий результат, используя функцию «Быстрый просмотр»:

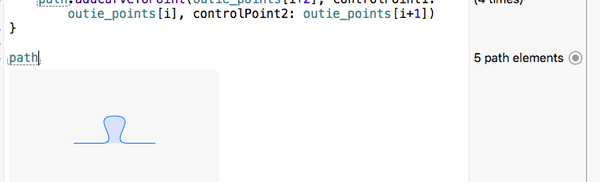
Все идет нормально. Как мы генерируем четыре стороны головоломки? Ответ (как вы можете догадаться), используя геометрические преобразования. Применяя поворот на 90 градусов с последующим соответствующим переводом к указанному выше path , мы можем легко создать остальные стороны.

Предостережение: проблема с внутренним наполнением

К сожалению, здесь есть одна оговорка. Преобразование не будет автоматически объединять отдельные сегменты. Несмотря на то, что силуэт нашего пазла выглядит хорошо, его интерьер не будет заполнен, и мы столкнемся с проблемами при использовании его в качестве маски. Мы можем наблюдать это на детской площадке. Добавьте следующий код:

« `javascript let transform = CGAffineTransformTranslate (CGAffineTransformMakeRotation (CGFloat (-M_PI / 2))), 0, размер)

пусть temppath = path.copy () как! UIBezierPath

let foursided = UIBezierPath () для i в 0… 3 {temppath.applyTransform (transform) foursided.appendPath (temppath)

}

четырехсторонний

Беглый взгляд показывает нам следующее:

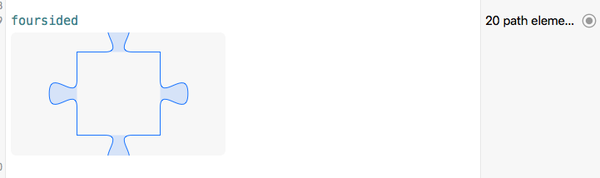
Обратите внимание, что внутренняя часть изделия не затенена, указывая, что она не была заполнена.

Вы можете узнать команды рисования, используемые для построения сложного UIBezierPath , изучив его свойство debugDescription на игровой площадке.

Решение проблемы заполнения

Геометрические преобразования в UIBezierPath работают достаточно хорошо для общего случая использования, то есть, когда у вас уже есть замкнутая фигура или фигура, которую вы трансформируете, изначально открыта, и вы хотите сгенерировать их геометрически преобразованные версии. Наш вариант использования отличается. Путь действует как подпуть в большей форме, которую мы строим и чей интерьер мы намереваемся заполнить. Это немного сложнее.

Один из подходов состоит в том, чтобы связываться с внутренними CGPathApply() пути (используя CGPathApply() из Core Graphics API) и вручную соединять сегменты вместе, чтобы в итоге получить единую замкнутую и правильно заполненную форму.

Но этот вариант выглядит немного хакерским, и поэтому я выбрал другой подход. Сначала мы применяем геометрические преобразования к самим точкам с помощью функции CGPointApplyAffineTransform() , применяя точно такое же преобразование, которое мы пытались использовать минуту назад. Затем мы используем преобразованные точки для создания подпути, который добавляется к общей фигуре. В конце урока мы увидим пример, в котором мы можем правильно применить геометрическое преобразование к пути Безье.

Генерация вариаций куска

Как мы генерируем вкладку «innie»? Мы могли бы снова применить геометрическое преобразование с отрицательным коэффициентом масштабирования в направлении y (инвертируя его форму), но я решил сделать это вручную, просто инвертировав координаты y точек в outie_points .

Что касается вкладки с плоскими краями, хотя я мог бы просто использовать отрезок прямой линии для ее представления, чтобы избежать необходимости специализировать код для отдельных случаев, я просто установил координату y каждой точки в outie_points равной нулю , Это дает нам:

javascript let innie_points = outie_points.map { CGPointMake($0.x, -$0.y) } let flat_points = outie_points.map { CGPointMake($0.x, 0) }

В качестве упражнения вы можете сгенерировать кривые Безье из этих краев и просмотреть их с помощью Quick Look.

Теперь вы знаете достаточно для меня, чтобы заморозить вас всем кодом, который связывает все вместе в одну функцию.

Замените все содержимое страницы игровой площадки следующим:

« `импорт JavaScript UIKit импорт XCPlayground

enum Edge {case Outie case Innie case Flat}

func jigsawPieceMaker (размер: CGFloat, ребра: [Edge]) -> UIBezierPath {

  func incrementalPathBuilder (firstPoint: CGPoint) -> ([CGPoint]) -> UIBezierPath {
     let path = UIBezierPath ()
     path.moveToPoint (FirstPoint)
     возвращение {
         указывает на
         подтвердить (points.count% 3 == 0)
         для меня в 0.stride (через: points.count - 3, by: 3) {
             path.addCurveToPoint (points [i + 2], controlPoint1: points [i], controlPoint2: points [i + 1])
         }
        
         Обратный путь
     }
 }


 let outie_coords: [(x: CGFloat, y: CGFloat)] = [/ * (0, 0), * / (1.0 / 9, 0), (2.0 / 9, 0), (1.0 / 3, 0), (37,0 / 60, 0), (1,0 / 6, 1,0 / 3), (1,0 / 2, 1,0 / 3), (5,0 / 6, 1,0 / 3), (23,0 / 60, 0), (2,0 / 3) , 0), (7,0 / 9, 0), (8,0 / 9, 0), (1,0, 0)]

 let outie_points = outie_coords.map {CGPointApplyAffineTransform (CGPointMake ($ 0.x, $ 0.y), CGAffineTransformMakeScale (размер, размер))}
 let innie_points = outie_points.map {CGPointMake ($ 0.x, - $ 0.y)}
 let flat_points = outie_points.map {CGPointMake ($ 0.x, 0)}

 var shapeDict: [Edge: [CGPoint]] = [.Outie: outie_points, .Innie: innie_points, .Flat: flat_points]


 let transform = CGAffineTransformTranslate (CGAffineTransformMakeRotation (CGFloat (-M_PI / 2)), 0, размер)
 let path_builder = incrementalPathBuilder (CGPointZero)
 var path: UIBezierPath!
 для края в краях {
     path = path_builder (shapeDict [edge]!)
    
     для (e, pts) в shapeDict {
         let tr_pts = pts.map {CGPointApplyAffineTransform ($ 0, преобразование)}
         shapeDict [e] = tr_pts
     }
 }

 path.closePath ()
 Обратный путь }

let piece1 = jigsawPieceMaker (размер: 100, ребра: [.Innie, .Outie, .lat, .Innie])

let piece2 = jigsawPieceMaker (размер: 100, ребра: [.Innie, .Innie, .Innie, .Innie]) piece2.applyTransform (CGAffineTransformMakeRotation (CGFloat (M_PI / 3)))

« `

В коде есть только несколько интересных вещей, которые я хотел бы уточнить:

• Мы используем enum для определения различных форм ребер. Мы сохраняем точки в словаре, который использует значения перечисления в качестве ключей.
• Мы объединяем подпути (состоящие из каждого края фигуры четырехстороннего пазла) в функции incrementalPathBuilder(_) , определенной внутри функции jigsawPieceMaker(size:edges:) .
• Теперь, когда кусок мозаики заполнен правильно, как мы видим в выводе applyTransform(_:) взгляда, мы можем смело использовать метод applyTransform(_:) чтобы применить геометрическое преобразование к фигуре. В качестве примера я применил вращение на 60 градусов ко второй части.

Вывод

Я надеюсь убедить вас в том, что возможность программно генерировать векторную графику может оказаться полезным в вашем арсенале. Надеюсь, вы будете вдохновлены продумывать (и кодировать) другие интересные приложения для векторной графики, которые вы можете включить в свои собственные приложения.