Статьи

Обработка графа: центральность между средами — шифр neo4j против графа потока

Февраль 23, 2019

На прошлой неделе я писал об алгоритме центральности промежуточности и моих попытках понять его с помощью graphstream, и, читая исходный код, я понял, что смогу что-то собрать, используя алгоритм всех кратчайших путей neo4j.

Напомним, что для определения нагрузки и важности узла в графе используется алгоритм центральности промежуточности.

Говоря об этом с Джен, она указала, что вычисление центральности между узлами по всему графу часто не имеет смысла. Тем не менее, может быть полезно узнать, какой узел является наиболее важным в меньшем подграфе, который вас интересует.

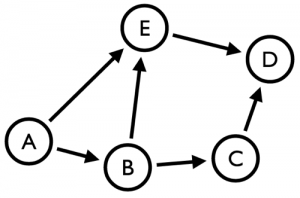
В этом случае меня интересует разработка центральности узлов между очень маленьким ориентированным графом:

betweeness2

Давайте кратко резюмируем алгоритм:

[Центральность между] равна числу кратчайших путей от всех вершин ко всем остальным, которые проходят через этот узел.

Это означает, что мы исключаем любые пути, которые идут напрямую между двумя узлами, не проходя через какие-либо другие, что я изначально не понимал.

Если мы разработаем соответствующие пути вручную, мы получим следующее:

01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
A -> B: Direct Path Exists
A -> C: B
A -> D: E
A -> E: Direct Path Exists
B -> A: No Path Exists
B -> C: Direct Path Exists
B -> D: E or C
B -> E: Direct Path Exists
C -> A: No Path Exists
C -> B: No Path Exists
C -> D: Direct Path Exists
C -> E: No Path Exists
D -> A: No Path Exists
D -> B: No Path Exists
D -> C: No Path Exists
D -> E: No Path Exists
E -> A: No Path Exists
E -> B: No Path Exists
E -> C: No Path Exists
E -> D: Direct Path Exists

Что дает следующие значения центральности промежуточности:

1
2
3
4
5
A: 0
B: 1
C: 0.5
D: 0
E: 1.5

Мы можем написать тест для последней версии graphstream (который учитывает направление), чтобы подтвердить наш ручной алгоритм:

01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
@Test
    public void calculateBetweennessCentralityOfMySimpleGraph() {
        Graph graph = new SingleGraph("Tutorial 1");
 
        Node A = graph.addNode("A");
        Node B = graph.addNode("B");
        Node E = graph.addNode("E");
        Node C = graph.addNode("C");
        Node D = graph.addNode("D");
 
        graph.addEdge("AB", A, B, true);
        graph.addEdge("BE", B, E, true);
        graph.addEdge("BC", B, C, true);
        graph.addEdge("ED", E, D, true);
        graph.addEdge("CD", C, D, true);
        graph.addEdge("AE", A, E, true);
 
        BetweennessCentrality bcb = new BetweennessCentrality();
        bcb.computeEdgeCentrality(false);
        bcb.betweennessCentrality(graph);
 
        System.out.println("A="+ A.getAttribute("Cb"));
        System.out.println("B="+ B.getAttribute("Cb"));
        System.out.println("C="+ C.getAttribute("Cb"));
        System.out.println("D="+ D.getAttribute("Cb"));
        System.out.println("E="+ E.getAttribute("Cb"));
    }

Результат, как и ожидалось:

1
2
3
4
5
A=0.0
B=1.0
C=0.5
D=0.0
E=1.5

Я хотел посмотреть, смогу ли я сделать то же самое, используя neo4j, поэтому я создал график в пустой базе данных, используя следующие операторы шифрования:

01
02
03
04
05
06
07
08
09
10
11
12
CREATE (A {name: "A"})
CREATE (B {name: "B"})
CREATE (C {name: "C"})
CREATE (D {name: "D"})
CREATE (E {name: "E"})
 
CREATE A-[:TO]->E
CREATE A-[:TO]->B
CREATE B-[:TO]->C
CREATE B-[:TO]->E
CREATE C-[:TO]->D
CREATE E-[:TO]->D

Затем я написал запрос, который нашел кратчайший путь между всеми наборами узлов в графе:

1
2
3
MATCH p = allShortestPaths(source-[r:TO*]->destination)
WHERE source <> destination
RETURN NODES(p)

Если мы запустим его, он вернет следующее:

01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
==> +---------------------------------------------------------+
==> | NODES(p)                                                |
==> +---------------------------------------------------------+
==> | [Node[1]{name:"A"},Node[2]{name:"B"}]                   |
==> | [Node[1]{name:"A"},Node[2]{name:"B"},Node[3]{name:"C"}] |
==> | [Node[1]{name:"A"},Node[5]{name:"E"},Node[4]{name:"D"}] |
==> | [Node[1]{name:"A"},Node[5]{name:"E"}]                   |
==> | [Node[2]{name:"B"},Node[3]{name:"C"}]                   |
==> | [Node[2]{name:"B"},Node[3]{name:"C"},Node[4]{name:"D"}] |
==> | [Node[2]{name:"B"},Node[5]{name:"E"},Node[4]{name:"D"}] |
==> | [Node[2]{name:"B"},Node[5]{name:"E"}]                   |
==> | [Node[3]{name:"C"},Node[4]{name:"D"}]                   |
==> | [Node[5]{name:"E"},Node[4]{name:"D"}]                   |
==> +---------------------------------------------------------+
==> 10 rows

Мы по-прежнему возвращаем прямые ссылки между узлами, но это довольно легко исправить, отфильтровав результаты по количеству узлов в пути:

1
2
3
MATCH p = allShortestPaths(source-[r:TO*]->destination)
WHERE source <> destination  AND LENGTH(NODES(p)) > 2
RETURN EXTRACT(n IN NODES(p): n.name)
1
2
3
4
5
6
7
8
9
==> +--------------------------------+
==> | EXTRACT(n IN NODES(p): n.name) |
==> +--------------------------------+
==> | ["A","B","C"]                  |
==> | ["A","E","D"]                  |
==> | ["B","C","D"]                  |
==> | ["B","E","D"]                  |
==> +--------------------------------+
==> 4 rows

Если мы немного настроим запрос на шифрование, мы сможем получить коллекцию кратчайших путей для каждого источника / назначения:

1
2
3
4
5
6
MATCH p = allShortestPaths(source-[r:TO*]->destination)
WHERE source <> destination  AND LENGTH(NODES(p)) > 2
WITH EXTRACT(n IN NODES(p): n.name) AS nodes
RETURN HEAD(nodes) AS source,
       HEAD(TAIL(TAIL(nodes))) AS destination,
       COLLECT(nodes) AS paths
1
2
3
4
5
6
7
8
==> +------------------------------------------------------+
==> | source | destination | paths                         |
==> +------------------------------------------------------+
==> | "A"    | "D"         | [["A","E","D"]]               |
==> | "A"    | "C"         | [["A","B","C"]]               |
==> | "B"    | "D"         | [["B","C","D"],["B","E","D"]] |
==> +------------------------------------------------------+
==> 3 rows

Когда у нас есть способ нарезать коллекции с использованием шифра, не составит труда перейти отсюда к показателю центральности узлов, но сейчас гораздо проще использовать общий язык программирования.

В этом случае я использовал Ruby и придумал следующий код:

01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
require 'neography'
neo = Neography::Rest.new
 
query =  " MATCH p = allShortestPaths(source-[r:TO*]->destination)"
query << " WHERE source <> destination  AND LENGTH(NODES(p)) > 2"
query << " WITH EXTRACT(n IN NODES(p): n.name) AS nodes"
query << " RETURN HEAD(nodes) AS source, HEAD(TAIL(TAIL(nodes))) AS destination, COLLECT(nodes) AS paths"
 
betweenness_centrality = { "A" => 0, "B" => 0, "C" => 0, "D" => 0, "E" => 0 }
 
neo.execute_query(query)["data"].map { |row| row[2].map { |path| path[1..-2] } }.each do |potential_central_nodes|     
  number_of_central_nodes = potential_central_nodes.size
  potential_central_nodes.each do |nodes|
    nodes.each { |node| betweenness_centrality[node] += (1.0 / number_of_central_nodes) }
  end
end
 
p betweenness_centrality

который выводит следующее:

1
2
$ bundle exec ruby centrality.rb
{"A"=>0, "B"=>1.0, "C"=>0.5, "D"=>0, "E"=>1.5}

Кажется, что он справляется с работой, но я уверен, что есть некоторые нереализованные случаи, о которых заботилась бы зрелая библиотека. В качестве эксперимента, чтобы увидеть, что возможно, я думаю, что это не так уж плохо!

График находится на консоли neo4j на тот случай, если кто- то захочет поиграть с ним.

40
Share: