В пространстве базы данных графа есть два типа механизмов обхода: локальный и распределенный. Механизмы локального обхода, как правило, предназначены для баз данных с одним механизмом графов и используются для производственных приложений реального времени. Механизмы распределенного обхода обычно предназначены для баз данных с несколькими машинными графами и используются для приложений пакетной обработки. Этот разрыв довольно острый в сообществе, но ничто не мешает объединению обеих моделей. Обсуждение этого разрыва и его унификация представлены в этом посте.
Местные двигатели обхода
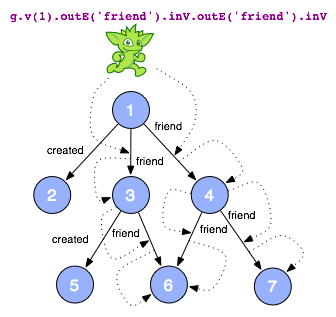
В локальном механизме обхода обычно существует один агент обработки, который подчиняется программе. Агент называется traverser, а следующая программа называется описанием пути . В Gremlin описание пути друга-друга определяется так:
g.v(1).outE('friend').inV.outE('friend').inV
Когда это описание пути интерпретируется обходчиком через граф, экземпляр описания реализуется как фактические пути в графе, которые соответствуют этому описанию. Например, обходчик Gremlin начинается с вершины 1 и затем переходит к своим исходящим друзьям- ребрам. Затем он будет перемещаться к вершинам головы / цели этих ребер (то есть вершинам 3 и 4). После этого, он будет идти к другу -ребре этих вершин и , наконец, к голове предыдущих ребер (т.е. вершина 6 и 7). Таким образом, один обходчик следует по всем путям, которые открываются при каждой новой операции атомарного графа (т. Е. Каждый новый шаг после.). Абстрактный синтаксис: step.step.step, То, что возвращается этим описанием пути друга-друга, на диаграмме примера, это вершины 6 и 7.
Во многих ситуациях это не желаемый конец пути, а некоторый побочный эффект обхода. Например, во время прогулки он может обновить некоторую глобальную структуру данных, такую как ранжирование вершин. Эта идея представлена в описании пути ниже, где путь outE.inV повторяется более 1000 раз. Каждый раз при прохождении вершины карта m обновляется. Эта глобальная карта m поддерживает ключи, которые являются вершинами, и значения, которые обозначают число раз, когда каждая вершина была затронута ( поведение groupCount ).
m = [:]
g.v(1).outE.inV.groupCount(m).loop(3){it.loops < 1000}
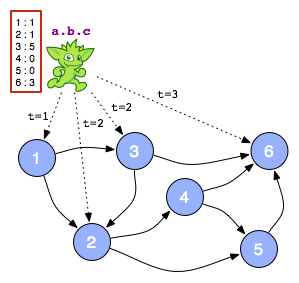
Схема механизма локального прохождения абстрактно изображена справа, где один обходчик подчиняется некоторому описанию пути ( abc ) и при этом перемещается по графику и обновляет глобальную структуру данных (красная коробка в рамке).
Учитывая необходимость перемещения переходов от элемента к элементу, графовые базы данных этой формы имеют тенденцию поддерживать сильную локальность данных посредством структуры данных графа прямой ссылки (т. Е. Вершины имеют указатели на ребра и ребра на вершины). Несколько примеров таких графовых баз данных включают Neo4j , OrientDB и DEX .
Распределенные двигатели обхода
В распределенном механизме обхода обход представлен в виде потока сообщений между элементами графа. Как правило, каждый элемент (например, вершина) работает независимо от других элементов. Каждый элемент рассматривается как собственный процессор с собственной (обычно однородной) программой для выполнения. Элементы общаются друг с другом посредством передачи сообщений . Когда больше сообщений не было передано, обход завершается, и результаты обхода обычно представляются в виде распределенной структуры данных по элементам. В базах данных графов такого типа обычно используется модель распределенных вычислений Bulk Synchronous Parallel . Каждый шаг синхронизируется способом, аналогичным такту в аппаратном обеспечении. Экземпляры этой модели включают Agrapa ,Pregel , Trinity и GoldenOrb .
Пример распределенного обхода графа теперь представлен с использованием алгоритма ранжирования в Java. [ ПРИМЕЧАНИЕ . В этом примере ребра не являются гражданами первого класса. Это типично для современного уровня техники в распределенных движках. Они, как правило, предназначены для однореляционных графов без меток.]
public void evaluateStep(int step) {
if(!this.inbox.isEmpty() && step < 1000) {
this.rank = this.rank + this.inbox.size();
for(Vertex vertex : this.adjacentVertices()) {
for(int i=0; i<this.inbox.size(); i++) {
this.sendMessage(vertex);
}
}
this.inbox.clear();
}
}
Каждой вершине предоставляется вышеуказанный кусок кода. Этот код выполняется каждой вершиной на каждом шаге (в смысле «Массовая синхронная параллель» — «тактовый цикл»). В конкретном примере «стартовое сообщение», скажем, для вершины 1 инициирует процесс. Вершина 1 будет увеличивать свой ранг на 1. Затем она будет отправлять сообщения в смежные вершины. На следующем шаге вершины, смежные с 1, обновляют свой ранг в соответствии с количеством сообщений, полученных на предыдущем шаге. Этот процесс продолжается до тех пор, пока в системе не будет найдено больше сообщений. Агрегирование всех значений ранга является результатом алгоритма. Общая схема шага «Массовая синхронная параллель»: 1.) получать сообщения 2.) обрабатывать сообщения 3.) отправлять сообщения.
Когда ребра помечены (например, друг, создан, приобретен и т. Д. — многореляционные графы ), необходимо иметь больший контроль над тем, как передаются сообщения. Другими словами, необходимо отфильтровать конкретные пути, исходящие из начальной вершины. Например, при обходе друга друга созданные края должны игнорироваться. Для этого можно представить себе использование языка Гремлин в механизме обхода распределенных графов. В этой модели шаг в Gremlin — это шаг в модели Bulk Synchronous Parallel.
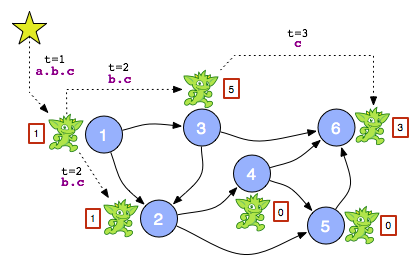
Учитывая работающий пример abc в модели локального движка, пример распределенного движка Gremlin-esque выглядит следующим образом. «Начальное сообщение» abc отправляется в вершину 1. Вершина 1 «выскакивает» на первом шаге a описания пути, а затем передает сообщение bc тем вершинам, которые удовлетворяют a . Таким образом, на шаге 2, вершины 2 и 3 имеют Ьс ждет их в своем почтовом ящике. Наконец, на шаге 3 вершина 6 получает сообщение c, Если желателен побочный эффект (например, ранжирование вершин), следует избегать глобальной структуры данных. Учитывая параллельный характер распределенных механизмов обхода, лучше всего избегать блокировки потоков при записи в глобальную структуру данных. Вместо этого каждая вершина может поддерживать часть структуры данных (красные прямоугольники). Более того, для нерегулярных описаний путей (требующих памяти) локальные структуры данных могут служить «блокнотом». Наконец, когда вычисление завершено, «понижающая» фаза может дать результаты ранга как совокупность компонентов структуры данных (объединение красных блоков).
В этой области предстоит проделать большую работу, и члены команды TinkerPop в настоящее время изучают объединение локальных и распределенных моделей обхода графа. Таким образом, некоторые этапы описания пути могут быть локальными, а затем другие могут быть «разветвлены» для параллельной работы. Мы находимся на краю наших мест, чтобы посмотреть, что выйдет из этого обхода мысли .
Подтверждения
Содержание этого поста было непосредственно вдохновлено беседами с Алексом Авербухом , Питером Нойбауэром , Андреасом Коллеггером и Рики Хо . Косвенное вдохновение пришло от моих разных соавторов и всех участников пространства TinkerPop .
Источник: http://markorodriguez.com/2011/04/19/local-and-distributed-traversal-engines/