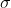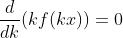Закон Бенфорда в настоящее время чрезвычайно популярен (см., Например, http://en.wikipedia.org/… ). Обычно утверждается, что для заданного набора данных изменение единиц не влияет на распределение первой цифры. Таким образом, это должно быть связано с масштабно-инвариантным распределением. Эвристически, масштабная (или единичная) инвариантность означает, что плотность меры 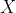
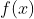
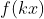
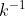
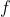
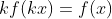
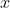
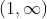
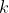
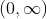
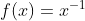
Теперь, если 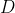
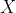
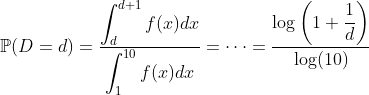
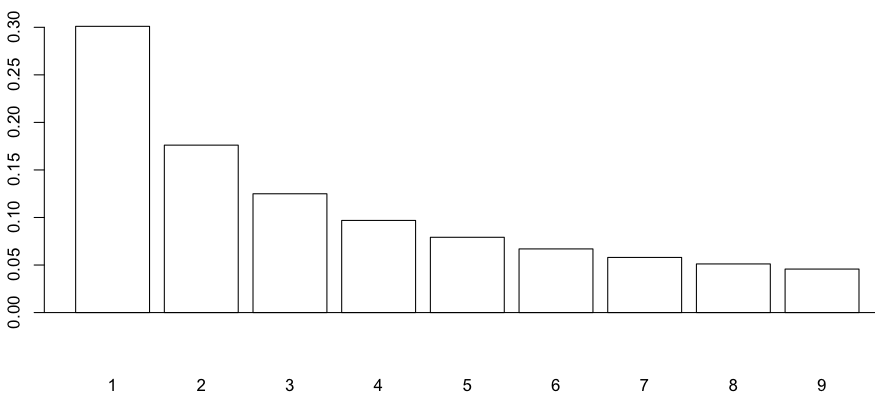
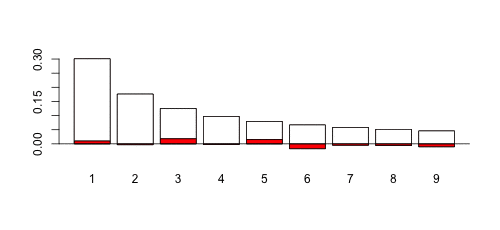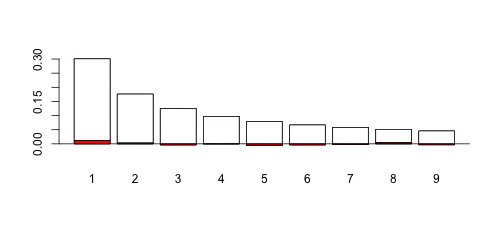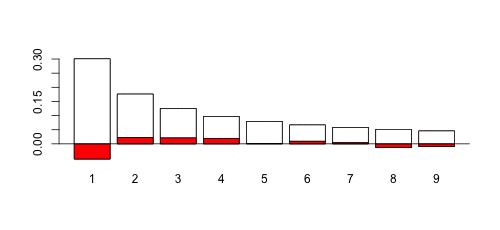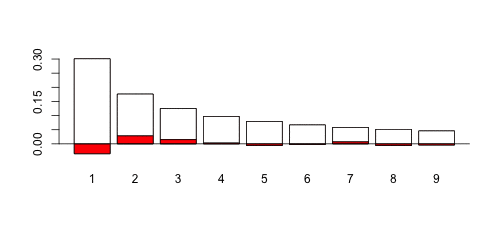
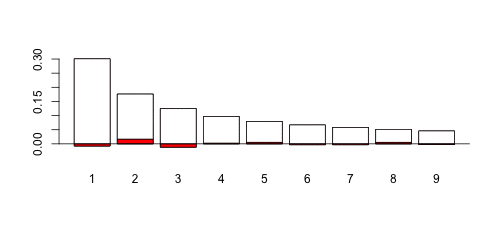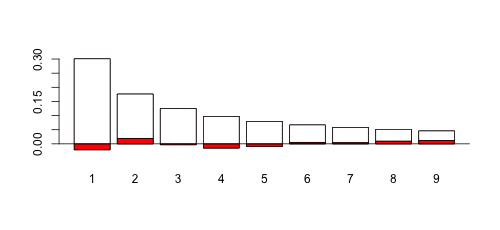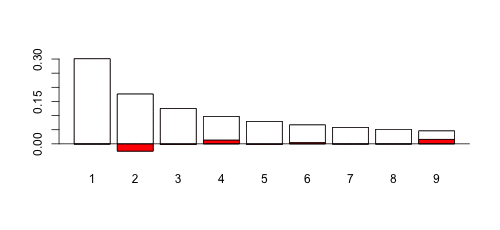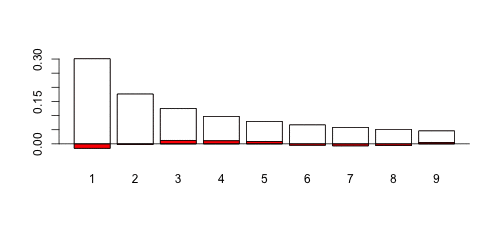
> (benford=log(1+1/(1:9))/log(10)) [1] 0.30103000 0.17609126 0.12493874 0.09691001 0.07918125 [6] 0.06694679 0.05799195 0.05115252 0.04575749 > names(benford)=1:9 > sum(benford) [1] 1 > barplot(benford,col="white",ylim=c(-.045,.3)) > abline(h=0)
Чтобы вычислить эмпирическое распределение из выборки, используйте следующую функцию
> firstdigit=function(x){
+ if(x>=1){x=as.numeric(substr(as.character(x),1,1)); zero=FALSE}
+ if(x<1){zero=TRUE}
+ while(zero==TRUE){
+ x=x*10; zero=FALSE
+ if(trunc(x)==0){zero=TRUE}
+ }
+ return(trunc(x))
+ }
а потом
> Xd=sapply(X,firstdigit) > table(Xd)/1000
В законе Бенфорда: эмпирическое исследование и новое объяснение мы можем прочитать
Это не математическая статья, поэтому не ожидайте никаких формальных доказательств в этой статье. По крайней мере, мы можем запустить симуляцию Монте-Карло и посмотреть, что происходит, если мы сгенерируем выборки из логнормального распределения с дисперсией 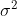
> set.seed(1)
> s=1
> X=rlnorm(n=1000,0,s)
> Xd=sapply(X,firstdigit)
> table(Xd)/1000
Xd
1 2 3 4 5 6 7 8 9
0.288 0.172 0.121 0.086 0.075 0.072 0.073 0.053 0.060
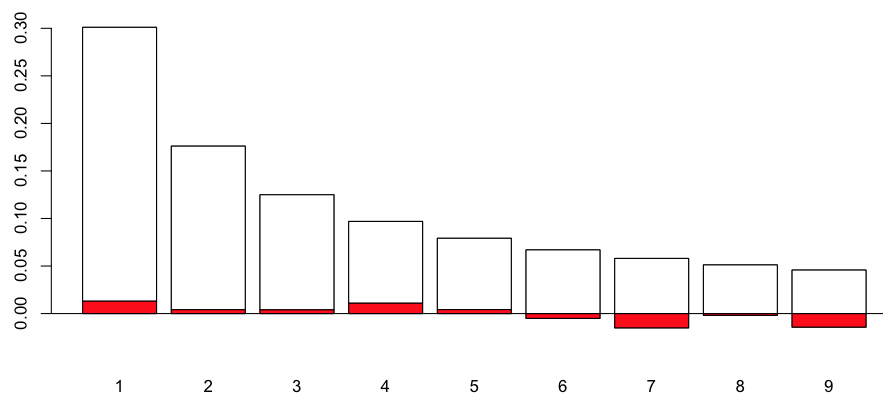
> T=rbind(benford,-table(Xd)/1000)
> barplot(T,col=c("red","white"),ylim=c(-.045,.3))
> abline(h=0)
Понятно, что это недалеко от закона Бенфорда. Возможно, можно рассмотреть более формальный тест, например, тест Пирсона 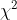
> chisq.test(T,p=benford) Chi-squared test for given probabilities data: T X-squared = 10.9976, df = 8, p-value = 0.2018
Так что да, закон Бенфорда допустим! Теперь, если мы рассмотрим случай, когда 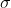
по сравнению со случаем, где 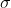
Можно сгенерировать несколько выборок (всегда одного размера, здесь 1000 наблюдений), просто изменить параметр дисперсии 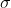
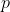
> T=table(Xd) > T=T[as.character(1:9)] > T[is.na(T)]=0 > PVAL[i]=chisq.test(T,p=benford)$p.value
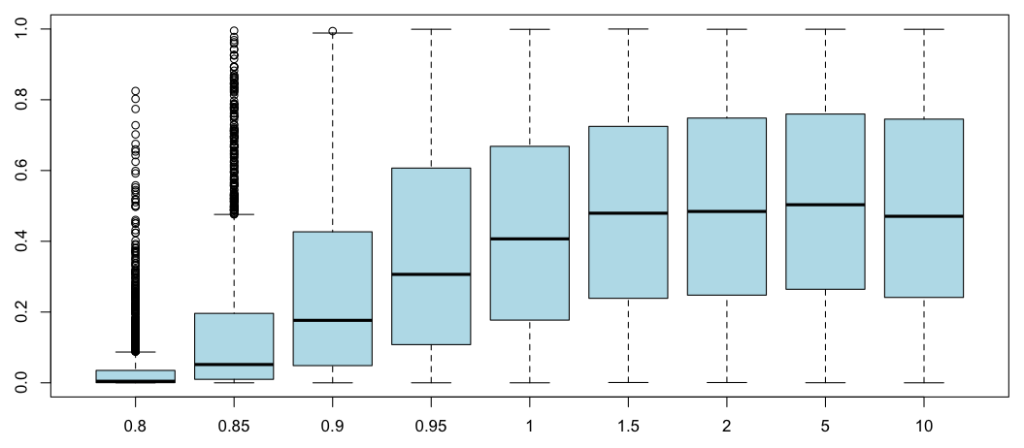
Боксплоты 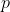
Когда 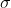
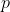
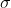
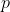
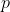
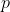
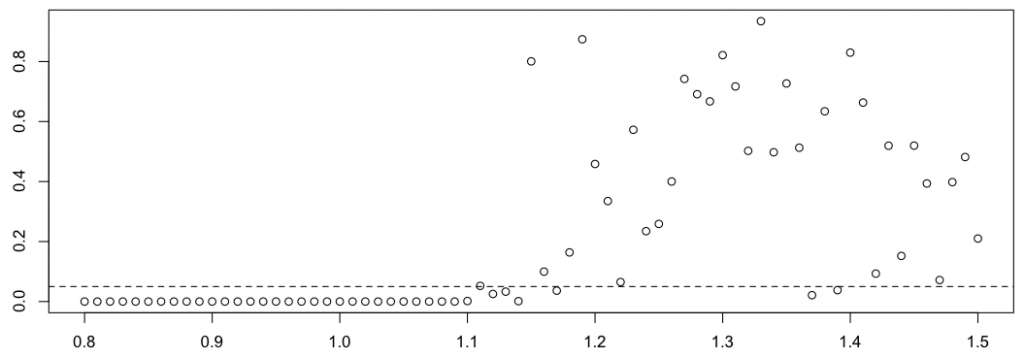
Обратите внимание, что также возможно вычислить 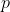
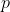
> ks.test(PVAL[,s], "punif")$p.value
Действительно, если