На прошлой неделе мы увидели, как принимать во внимание подверженность для вычисления непараметрических оценок нескольких величин (эмпирических средних и эмпирических отклонений), включающих подверженность. Давайте посмотрим, что можно сделать, если мы хотим смоделировать биномиальный ответ. Модель здесь следующая:
- количество претензий
за период
- количество претензий
на
)
что можно визуализировать ниже
Рассмотрим случай, когда переменная интереса — это не количество претензий, а просто показатель возникновения претензии. Затем мы хотим смоделировать событие 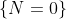
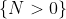
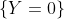
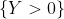
Словом, это означает, что вероятность отсутствия претензии в первые шесть месяцев года является квадратным корнем из-за отсутствия претензии в течение года. Что имеет смысл. Предположим, что вероятность отсутствия заявки может быть объяснена некоторыми ковариатами, обозначенными 
Теперь, так как мы наблюдаем 
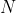
Набор данных, который мы будем использовать, всегда один и тот же
> sinistre=read.table("http://freakonometrics.free.fr/sinistreACT2040.txt", + header=TRUE,sep=";") > sinistres=sinistre[sinistre$garantie=="1RC",] > sinistres=sinistres[sinistres$cout>0,] > contrat=read.table("http://freakonometrics.free.fr/contractACT2040.txt", + header=TRUE,sep=";") > T=table(sinistres$nocontrat) > T1=as.numeric(names(T)) > T2=as.numeric(T) > nombre1 = data.frame(nocontrat=T1,nbre=T2) > I = contrat$nocontrat%in%T1 > T1= contrat$nocontrat[I==FALSE] > nombre2 = data.frame(nocontrat=T1,nbre=0) > nombre=rbind(nombre1,nombre2) > sinistres = merge(contrat,nombre) > sinistres$nonsin = (sinistres$nbre==0)
Первая модель, которую мы можем рассмотреть, основана на стандартном логистическом подходе , т.е.
Это хорошо, но сложно справиться со стандартными функциями. Тем не менее, всегда можно численно вычислить оценку максимального правдоподобия 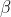
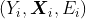
> Y=sinistres$nonsin > X=cbind(1,sinistres$ageconducteur) > E=sinistres$exposition > logL = function(beta){ + pi=(exp(X%*%beta)/(1+exp(X%*%beta)))^E + -sum(log(dbinom(Y,size=1,prob=pi))) + } > optim(fn=logL,par=c(-0.0001,-.001), + method="BFGS") $par [1] 2.14420560 0.01040707 $value [1] 7604.073 $counts function gradient 42 10 $convergence [1] 0 $message NULL > parametres=optim(fn=logL,par=c(-0.0001,-.001), + method="BFGS")$par
Теперь давайте посмотрим на альтернативы, основанные на стандартных регрессионных моделях. Например, модель биномиального журнала . Поскольку экспозиция представляется как степень годовой вероятности, все было бы хорошо, если бы 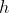
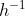
Теперь, если мы попытаемся закодировать его, это быстро станет проблематичным,
> reg=glm(nonsin~ageconducteur+offset(exposition), + data=sinistresI,family=binomial(link="log")) Error: no valid set of coefficients has been found: please supply starting values
Я пытался (почти) все, что мог, но я не мог избавиться от этого сообщения об ошибке,
> startglm=c(0,-.001) > names(startglm)=c("(Intercept)","ageconducteur") > etaglm=rep(-.01,nrow(sinistresI)) > etaglm[sinistresI$nonsin==0]=-10 > muglm=exp(etaglm) > reg=glm(nonsin~ageconducteur+offset(exposition), + data=sinistresI,family=binomial(link="log"), + control = glm.control(epsilon=1e-5,trace=TRUE,maxit=50), + start=startglm, + etastart=etaglm,mustart=muglm) Deviance = NaN Iterations - 1 Error: no valid set of coefficients has been found: please supply starting values
Поэтому я решил сдаться. Почти. На самом деле, проблема заключается в том, что 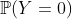
где 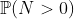
Здесь экспозиция больше не отображается как степень вероятности, а появляется мультипликативно. Конечно, есть условия более высокого порядка. Но давайте забудем их (пока). Если — еще раз — мы рассмотрим функцию связи журнала, то мы можем включить экспозицию или, если быть более точным, логарифм экспозиции.
> regopp=glm((1-nonsin)~ageconducteur+offset(log(exposition)), + data=sinistresI,family=binomial(link="log"))
который сейчас работает отлично.
Теперь, чтобы увидеть окончательную модель, возможно, нам следует вернуться к нашей модели регрессии Пуассона, поскольку у нас есть модель вероятности этого 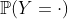
> regpois=glm(nbre~ageconducteur+offset(log(exposition)), + data=sinistres,family=poisson(link="log"))
Теперь мы можем сравнить эти три модели. Возможно, мы должны также включить прогноз без какой-либо объяснительной переменной. Для второй модели (на самом деле она работает без какой-либо пояснительной переменной), мы запускаем
> regreff=glm((1-nonsin)~1+offset(log(exposition)), + data=sinistres,family=binomial(link="log"))
так что прогноз здесь
> exp(coefficients(regreff)) (Intercept) 0.06776376
Это значение сопоставимо с логистической регрессией,
> logL2 = function(beta){ + pi=(exp(beta)/(1+exp(beta)))^E + -sum(log(dbinom(Y,size=1,prob=pi)))} > param=optim(fn=logL2,par=.01,method="BFGS")$par > 1-exp(param)/(1+exp(param)) [1] 0.06747777
Но сильно отличается от модели Пуассона,
> exp(coefficients(glm(nbre~1+offset(log(exposition)), + data=sinistres,family=poisson(link="log")))) (Intercept) 0.07279295
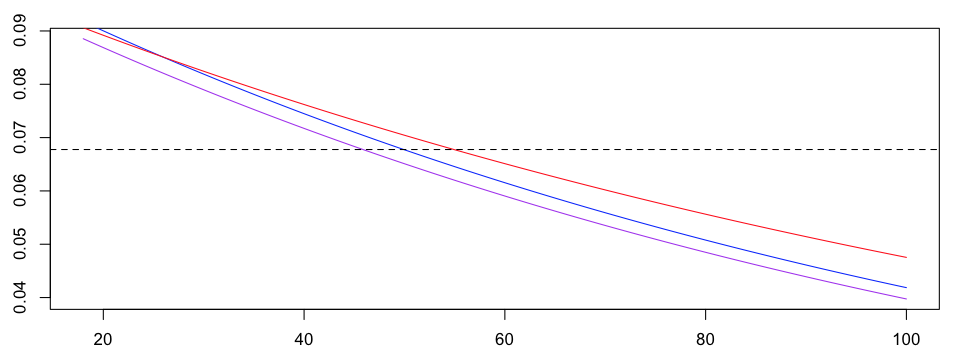
Давайте создадим график, чтобы сравнить эти модели,
> age=18:100 > yml1=exp(parametres[1]+parametres[2]*age)/(1+exp(parametres[1]+parametres[2]*age)) > plot(age,1-yml1,type="l",col="purple") > yp=predict(regpois,newdata=data.frame(ageconducteur=age, + exposition=1),type="response") > yp1=1-exp(-yp) > ydl=predict(regopp,newdata=data.frame(ageconducteur=age, + exposition=1),type="response") > plot(age,ydl,type="l",col="red") > lines(age,yp1,type="l",col="blue") > lines(age,1-yml1,type="l",col="purple") > abline(h=exp(coefficients(regreff)),lty=2)
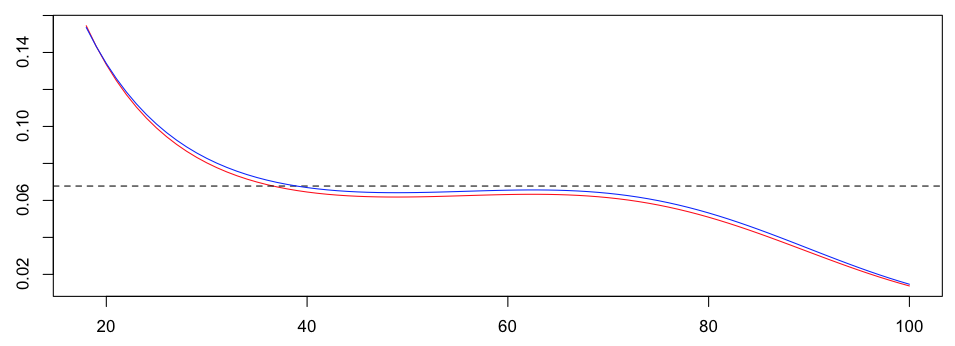
Обратите внимание, что три модели совершенно разные. На самом деле, с двумя моделями можно проводить более сложную регрессию, например, с помощью сплайнов, чтобы визуализировать влияние возраста на вероятность того, случится автомобильная авария или нет. Если мы сравним регрессию Пуассона (все еще в красном) и лог-биномиальную модель, с расширением Тейлора, мы получим
Следующий шаг — увидеть, как включить экспозицию в дерево. Но это другая история …
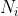 за период
за период 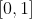
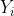 на
на 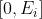 )
)
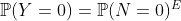




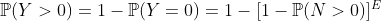
![http://latex.codecogs.com/gif.latex?\mathbb{P}(Y%3E0)\sim1-1+E\cdot%20\mathbb{P}(N%3E0)>=E\cdot% 20 \ mathbb {P} (N% 3E0)]](/wp-content/uploads/images/dzo/81083a949f05e9d36bb563b92bc867dd.latex)