Можно пойти дальше — намного дальше — на ограничивающие суммы случайных величин (упомянутых в предыдущем посте ). Например, если в предыдущем посте все было определено для распределений 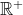
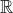
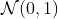
> Finv=function(u) qnorm(u,0,1)
> Ginv=function(u) qnorm(u,0,1)
> n=1000
> Qinf=Qsup=rep(NA,n-1)
> for(i in 1:(n-1)){
+ J=0:i
+ Qinf[i]=max(Finv(J/n)+Ginv((i-J)/n))
+ J=(i-1):(n-1)
+ Qsup[i]=min(Finv((J+1)/n)+Ginv((i-1-J+n)/n))
+ }
На самом деле, здесь можно сравнить с двумя простыми случаями: независимый случай, когда сумма имеет 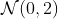
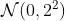
> lines(x,qnorm(x,sd=sqrt(2)),col="blue",lty=2) > lines(x,qnorm(x,sd=2),col="blue",lwd=2)
На приведенном ниже графике комонотонный случай (обычно рассматриваемый как сценарий наихудшего случая) представляет собой простую синюю линию (здесь показана анимация, иллюстрирующая сходимость численного алгоритма)
Ниже этой (сильной) синей линии риски субаддитивны для значения риска, т.е.
но выше, риски супераддитивны для стоимости на риск. т.е.
(поскольку для комонотонных вариаций квантиль суммы является суммой квантилей). Можно представить эти два случая выше, выделив зеленым цветом область, где риски являются сверхаддитивными, в то время как желтая область означает, что риски являются субаддитивными.
Напомним, что с гауссовским случайным вектором, с корреляцией, 
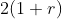
Но зеленая область также может быть получена, когда мы суммируем две гауссовские переменные! Нам просто нужно выйти за пределы гауссовского мира и рассмотреть еще одну связку.
Другое дело, что в предыдущем посте 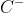
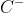
за все 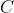
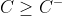
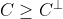
Что означает, что у нас должны быть более четкие границы. Численно можно рассчитать эти более четкие границы для квантилей. Нижняя граница становится
в то время как верхняя граница
Опять же, можно легко вычислить эти величины на сетке единичного интервала,
> Qinfind=Qsupind=rep(NA,n-1)
> for(i in 1:(n-1)){
+ J=1:(i)
+ Qinfind[i]=max(Finv(J/n)+Ginv((i-J)/n/(1-J/n)))
+ J=(i):(n-1)
+ Qsupind[i]=min(Finv(J/n)+Ginv(i/J))
+ }
Ниже приведен график (синяя область здесь для иллюстрации того, насколько четкими становятся эти границы в предположении, что у нас действительно есть положительная зависимость, эта область была достигнута только при связках с неположительной зависимостью)
Для высоких квантилей верхняя граница довольно близка к той, что была у нас ранее, поскольку наихудший случай, вероятно, получается, когда у нас есть положительная корреляция. Но это сильно повлияет на нижнюю границу. Например, теперь становится невозможным иметь отрицательный квантиль, когда вероятность превышает 75%, если у нас есть положительная зависимость …
> Qinfind[u==.75] [1] 0

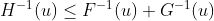
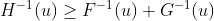


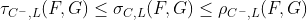
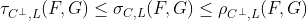
![http://latex.codecogs.com/gif.latex?\sup_ {и \ в [х, 1]} \ влево \ {F ^ {-1} (и) + G ^ {-1} \ влево (\ гидроразрыва {х} {и} \ справа) \ право \}](/wp-content/uploads/images/dzo/42ad15a8d71d1f04711ba29f142f16de.latex)
![http://latex.codecogs.com/gif.latex?\sup_ {и \ в [0, х]} \ влево \ {F ^ {-1} (и) + G ^ {-1} \ влево (\ гидроразрыва {хи} {1-у} \ справа) \ право \}](/wp-content/uploads/images/dzo/ca28490ff4f7d9c902c03be466afc54d.latex)
