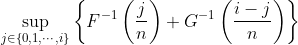Для последнего курса MAT8886 этого (длинного) зимнего сеанса по связкам (и крайним значениям) мы обсудим агрегацию рисков. Курс будет в основном посвящен проблеме ограничения распределения (или некоторой меры риска, скажем, Value-at-Risk) для двух случайных величин с заданным предельным распределением. Например, у нас есть два гауссовских риска. Какой может быть наихудший сценарий для квантиля 99% суммы? Обратите внимание, что я упоминаю последствия с точки зрения управления рисками, но, конечно, эти вопросы чрезвычайно важны с точки зрения статистического вывода, см., Например, Fan & Park (2006) .
Эта проблема иногда связана с каким-то вопросом, заданным Колмогоровым почти сто лет назад, как упоминалось у Макарова (1981) . Через год Рюшендорф (1982) также предложил доказательство расчета границ. Здесь мы сосредоточимся на измерении 2. Как обычно, это простой случай. Но, как упоминалось недавно, в Kreinovich & Ferson (2005) , в измерении 3 (или выше), « вычисление наилучших возможных границ для произвольного n является NP-сложной (вычислительно неразрешимой) задачей ». Итак, давайте сосредоточимся на случае, когда мы суммируем (только) две случайные величины (для тех, кто интересуется более высокой размерностью, Puccetti & Rüschendorf (2012) предоставили интересные результаты для двойной версии этих оптимальных границ).
Обозначим 
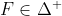
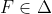

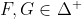
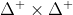
![http://latex.codecogs.com/gif.latex?T:[0,1]\times[0,1]\rightarrow[0,1]](/wp-content/uploads/images/dzo/91d18f2f7ad7c36964cfc72f97ae5e39.latex)
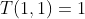
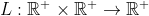
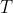
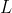
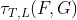
Один интересный случай может быть получен , когда 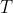
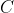
и далее можно написать
Также можно рассмотреть другие (общие) операторы, например, на основе суммы
или по минимуму,
где 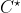
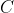
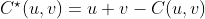
и аналогично
Все это кажется слишком теоретическим? Приложением может быть случай суммы, т. Е. 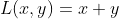
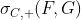
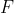

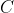
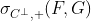
Важный результат (который можно найти в главе 7, в работе Schweizer and Sklar (1983) ) заключается в том, что, учитывая оператор 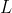
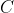
а также верхняя граница
Эти неравенства исходят из того , что для все связки 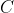
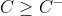
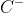
В случае суммы двух случайных величин, с предельными распределениями 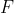

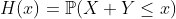
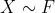

для нижней границы, и
для верхней границы. И эти границы четкие, в том смысле, что для всех 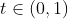
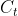
и есть (другая) связка 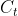
Таким образом, используя эти результаты, можно связать накопительную функцию распределения. Но на самом деле все это можно сделать и на квантилях (см. Frank, Nelsen & Schweizer (1987)). Для всех 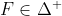
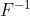
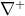
и
Эти определения действительно двойственные версии предыдущих, в том смысле, что ![http://latex.codecogs.com/gif.latex?\tau^{-1}_{T,L}(F^{-1},G^{-1})=[\tau_{T,L } (F, G)] ^ {- 1}](/wp-content/uploads/images/dzo/2ed874440ebed27bbc4fdc979ad93513.latex)
![http://latex.codecogs.com/gif.latex?\rho^{-1}_{T,L}(F^{-1},G^{-1})=[\rho_{T,L } (F, G)] ^ {- 1}](/wp-content/uploads/images/dzo/c6d32ac4b11be2c40493ecddbd30a5fb.latex)
Обратите внимание, что если мы сосредоточимся на суммах двумерных распределений, нижняя граница квантиля суммы
в то время как верхняя граница
Самое замечательное то, что не должно быть слишком сложно вычислять эти количества численно. Возможно, немного больше для кумулятивных функций распределения, поскольку они не определены на ограниченной основе. Но, тем не менее, если целью является, например, наложение этих границ 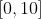
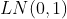
> F=function(x) plnorm(x,0,1)
> G=function(x) plnorm(x,0,1)
> n=100
> X=seq(0,10,by=.05)
> Hinf=Hsup=rep(NA,length(X))
> for(i in 1:length(X)){
+ x=X[i]
+ U=seq(0,x,by=1/n); V=x-U
+ Hinf[i]=max(pmax(F(U)+G(V)-1,0))
+ Hsup[i]=min(pmin(F(U)+G(V),1))}
Если мы построим эти границы, мы получим:
> plot(X,Hinf,ylim=c(0,1),type="s",col="red") > lines(X,Hsup,type="s",col="red")
Но каким-то образом работать с квантилями еще проще, поскольку они определены на конечной опоре. Квантили здесь:
> Finv=function(u) qlnorm(u,0,1) > Ginv=function(u) qlnorm(u,0,1)
Идея будет состоять в том, чтобы рассмотреть дискретизированную версию единичного интервала, как обсуждалось в Williamson (1989) , в гораздо более общем контексте. Опять же, идея состоит в том, чтобы вычислить, например,
Идея заключается в том , чтобы рассмотреть 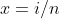
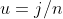
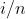
Код для вычисления этих границ для заданного 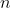
> n=1000
> Qinf=Qsup=rep(NA,n-1)
> for(i in 1:(n-1)){
+ J=0:i
+ Qinf[i]=max(Finv(J/n)+Ginv((i-J)/n))
+ J=(i-1):(n-1)
+ Qsup[i]=min(Finv((J+1)/n)+Ginv((i-1-J+n)/n))
+ }
Здесь мы имеем (несколько 
Здесь у нас есть простой код для визуализации границ квантилей на сумму двух рисков. Но можно пойти дальше …
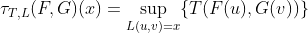
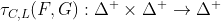
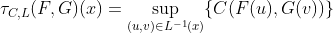
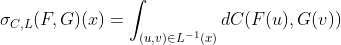
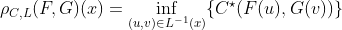
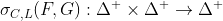
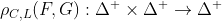
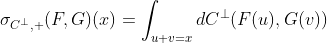
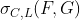
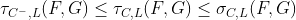
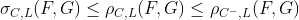
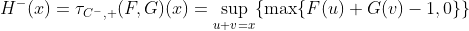
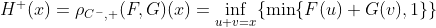

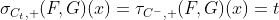
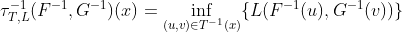
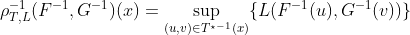
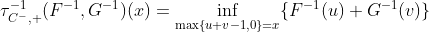
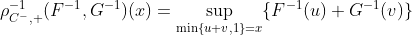

![http://latex.codecogs.com/gif.latex?\sup_ {и \ в [0, х]} \ {F ^ {-1} (и) + G ^ {-1} (Xu) \}](/wp-content/uploads/images/dzo/bc9bbd2df5fb773b762b801eae69cad2.latex)