Регрессия — это статистический метод, который помогает квалифицировать отношения между взаимосвязанными экономическими переменными. Первый шаг включает в себя оценку коэффициента независимой переменной, а затем измерение достоверности оцененного коэффициента. Это требует формулирования гипотезы, и на основе гипотезы мы можем создать функцию.
Если менеджер хочет определить взаимосвязь между рекламными расходами фирмы и доходами от продаж, он подвергнется проверке гипотезы. Предполагая, что более высокие расходы на рекламу приводят к увеличению продаж для фирмы. Менеджер собирает данные о расходах на рекламу и о выручке от продаж за определенный период времени. Эта гипотеза может быть переведена в математическую функцию, где она приводит к —
Y = A + Bx
Где Y — продажи, x — расходы на рекламу, A и B — постоянные.
После перевода гипотезы в функцию основание для этого должно найти связь между зависимой и независимой переменными. Значение зависимой переменной имеет наибольшее значение для исследователей и зависит от значения других переменных. Независимая переменная используется для объяснения изменения зависимой переменной. Это может быть классифицировано в два типа —
-
Простая регрессия — одна независимая переменная
-
Множественная регрессия — несколько независимых переменных
Простая регрессия — одна независимая переменная
Множественная регрессия — несколько независимых переменных
Простая регрессия
Ниже приведены шаги для построения регрессионного анализа —
- Укажите модель регрессии
- Получить данные о переменных
- Оценить количественные отношения
- Проверьте статистическую значимость результатов
- Использование результатов в принятии решений
Формула для простой регрессии —
Y = a + bX + u
Y = зависимая переменная
X = независимая переменная
а = перехват
б = уклон
и = случайный фактор
Данные поперечного сечения предоставляют информацию о группе объектов в данный момент времени, тогда как данные временных рядов предоставляют информацию об одном объекте с течением времени. Когда мы оцениваем уравнение регрессии, оно включает в себя процесс определения наилучшей линейной зависимости между зависимой и независимой переменными.
Метод обыкновенных наименьших квадратов (OLS)
Обычный метод наименьших квадратов предназначен для подгонки линии через разброс точек таким образом, чтобы сумма квадратов отклонений точек от линии сводилась к минимуму. Это статистический метод. Обычно программные пакеты выполняют оценку OLS.
Y = a + bX
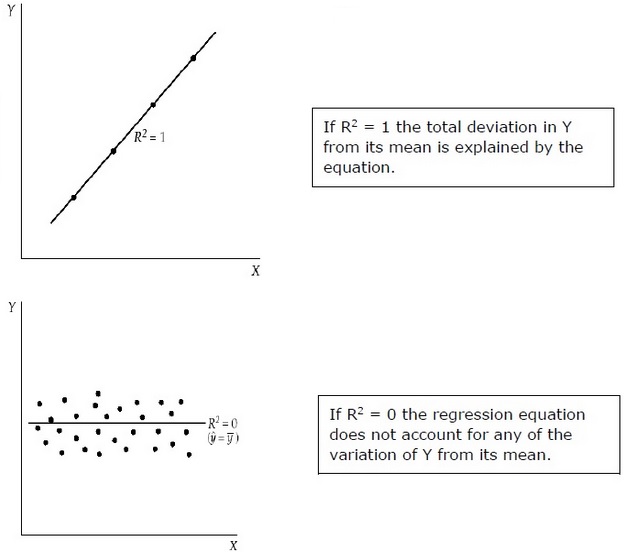
Коэффициент определения (R 2 )
Коэффициент детерминации — это мера, которая показывает процент изменения зависимой переменной из-за изменений в независимых переменных. R 2 является показателем качества модели соответствия. Ниже приведены методы —
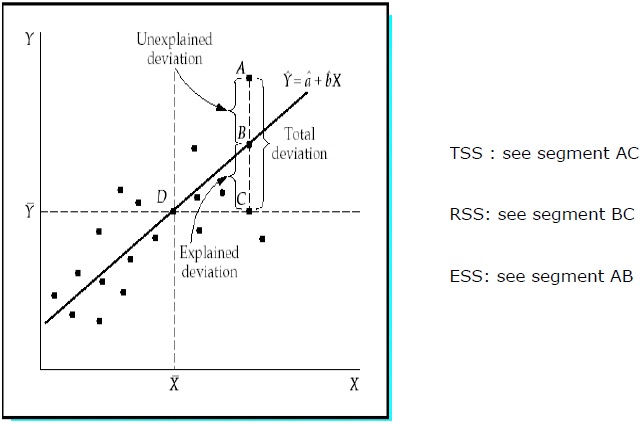
Общая сумма квадратов (TSS)
Сумма квадратов отклонений значений выборки Y от среднего значения Y.
TSS = SUM (Y i — Y) 2
Y i = зависимые переменные
Y = среднее значение зависимых переменных
я = количество наблюдений
Регрессия Сумма квадратов (RSS)
Сумма квадратов отклонений расчетных значений Y от среднего значения Y.
RSS = СУММА (Ỷ i — uY) 2
Ỷ i = оценочное значение Y
Y = среднее значение зависимых переменных
я = количество вариантов
Ошибка суммы квадратов (ESS)
Сумма квадратов отклонений выборочных значений Y от расчетных значений Y.
ESS = СУММА (Y i — Ỷ i ) 2
Ỷ i = оценочное значение Y
Y i = зависимые переменные
я = количество наблюдений
= 1 —
R 2 измеряет долю общего отклонения Y от его среднего значения, что объясняется регрессионной моделью. Чем ближе R 2 к единице, тем больше объясняющая сила уравнения регрессии. Значение R 2, близкое к 0, указывает на то, что уравнение регрессии будет иметь очень мало объяснительной силы.
Для оценки коэффициентов регрессии используется выборка из совокупности, а не всей совокупности. Важно делать предположения о населении на основе выборки и делать выводы о том, насколько хороши эти предположения.
Оценка коэффициентов регрессии
Каждая выборка из населения генерирует свой собственный перехват. Для расчета статистической разницы можно использовать следующие методы:
Двуххвостый тест —
Нулевая гипотеза: H 0 : b = 0
Альтернативная гипотеза: H a : b ≠ 0
Один хвостатый тест —
Нулевая гипотеза: H 0 : b> 0 (или b <0)
Альтернативная гипотеза: H a : b <0 (или b> 0)
Статистический тест —
б = расчетный коэффициент
E (b) = b = 0 (нулевая гипотеза)
SE b = стандартная ошибка коэффициента
,
Значение t зависит от степени свободы, одного или двух неудачных испытаний и уровня значимости. Для определения критического значения t можно использовать t-таблицу. Затем идет сравнение t-значения с критическим значением. Нужно отклонить нулевую гипотезу, если абсолютное значение статистического теста больше или равно критическому t-значению. Не отвергайте нулевую гипотезу, если абсолютное значение статистического теста меньше критического t-значения.
Множественный регрессионный анализ
В отличие от простой регрессии в множественном регрессионном анализе, коэффициенты указывают на изменение зависимых переменных, предполагая, что значения других переменных постоянны.
Тест статистической значимости называется F-тестом . F-тест полезен, поскольку он измеряет статистическую значимость всего уравнения регрессии, а не только для отдельного человека. Здесь В нулевой гипотезе нет никакой связи между зависимой переменной и независимыми переменными совокупности.
Формула — H 0 : b1 = b2 = b3 =…. = bk = 0
Не существует никакой связи между зависимой переменной и k независимыми переменными для совокупности.
F-тест статический —
F= frac left( fracR2K right) frac(1−R2)(nk−1)
Критическое значение F зависит от числителя и знаменателя, степени свободы и уровня значимости. F-таблица может быть использована для определения критического значения F. По сравнению с F – значением с критическим значением (F *) —
Если F> F *, нам нужно отвергнуть нулевую гипотезу.
Если F <F *, не отклоняйте нулевую гипотезу, так как нет существенной связи между зависимой переменной и всеми независимыми переменными.