Целью кластеризации k-средних является разделение n наблюдений на k кластеров, в которых каждое наблюдение принадлежит кластеру с ближайшим средним значением, служащим прототипом кластера. Это приводит к разбиению пространства данных на ячейки Вороного.
При заданном наборе наблюдений (x 1 , x 2 ,…, x n ) , где каждое наблюдение представляет собой вещественный реальный вектор в d-измерении, кластеризация k-средних имеет целью разделить n наблюдений на k групп G = {G 1 , G 2 ,…, G k }, чтобы минимизировать сумму квадратов в пределах кластера (WCSS), определенную следующим образом:
argmin sumki=1 sumx inSi параллельныйx− mui параллельный2
Последняя формула показывает целевую функцию, которая минимизируется для того, чтобы найти оптимальные прототипы в кластеризации k-средних. Интуиция формулы заключается в том, что мы хотели бы найти группы, которые отличаются друг от друга, и каждый член каждой группы должен быть похож на других членов каждого кластера.
В следующем примере показано, как запустить алгоритм кластеризации k-средних в R.
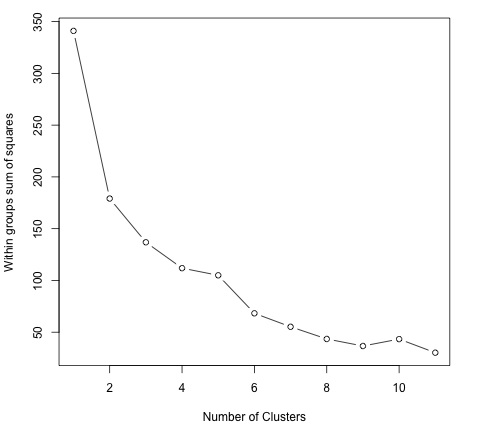
library(ggplot2) # Prepare Data data = mtcars # We need to scale the data to have zero mean and unit variance data <- scale(data) # Determine number of clusters wss <- (nrow(data)-1)*sum(apply(data,2,var)) for (i in 2:dim(data)[2]) { wss[i] <- sum(kmeans(data, centers = i)$withinss) } # Plot the clusters plot(1:dim(data)[2], wss, type = "b", xlab = "Number of Clusters", ylab = "Within groups sum of squares")
Чтобы найти хорошее значение для K, мы можем построить сумму квадратов внутри групп для различных значений K. Эта метрика обычно уменьшается при добавлении большего количества групп, мы хотели бы найти точку, в которой уменьшение суммы внутри групп квадратов начинает медленно уменьшаться. На графике это значение лучше всего представить как K = 6.
Теперь, когда значение K определено, необходимо запустить алгоритм с этим значением.