Первый подход к анализу данных — это визуальный анализ. Цели при этом обычно заключаются в нахождении отношений между переменными и одномерном описании переменных. Мы можем разделить эти стратегии как —
- Одномерный анализ
- Многомерный анализ
Одномерные графические методы
Одномерный — это статистический термин. На практике это означает, что мы хотим анализировать переменную независимо от остальных данных. Сюжеты, которые позволяют сделать это эффективно, —
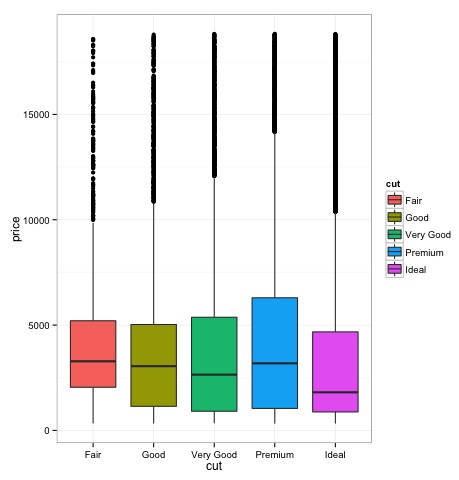
Box-участки
Боксы обычно используются для сравнения распределений. Это отличный способ визуально проверить, есть ли различия между дистрибутивами. Мы можем увидеть, если есть различия между ценами на бриллианты для разных огранки.
# We will be using the ggplot2 library for plotting
library(ggplot2)
data("diamonds")
# We will be using the diamonds dataset to analyze distributions of numeric variables
head(diamonds)
# carat cut color clarity depth table price x y z
# 1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43
# 2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31
# 3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31
# 4 0.29 Premium I VS2 62.4 58 334 4.20 4.23 2.63
# 5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75
# 6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48
### Box-Plots
p = ggplot(diamonds, aes(x = cut, y = price, fill = cut)) +
geom_box-plot() +
theme_bw()
print(p)
Как видно на графике, существуют различия в распределении цен на алмазы в разных видах огранки.
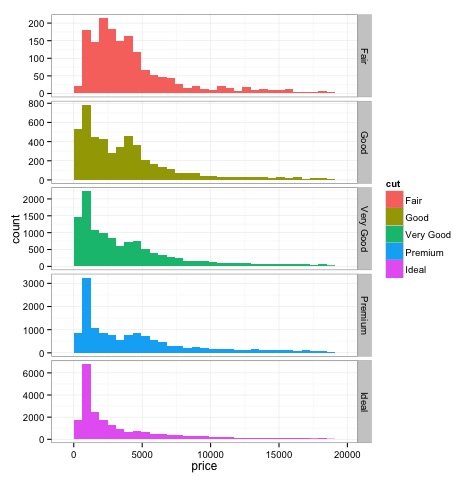
Гистограммы
source('01_box_plots.R')
# We can plot histograms for each level of the cut factor variable using
facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ .) +
theme_bw()
p
# the previous plot doesn’t allow to visuallize correctly the data because of
the differences in scale
# we can turn this off using the scales argument of facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ ., scales = 'free') +
theme_bw()
p
png('02_histogram_diamonds_cut.png')
print(p)
dev.off()
Вывод вышеприведенного кода будет следующим:
Многовариантные графические методы
Многовариантные графические методы в исследовательском анализе данных имеют целью найти взаимосвязи между различными переменными. Есть два способа сделать это, которые обычно используются: построение матрицы корреляции числовых переменных или просто построение необработанных данных в виде матрицы диаграмм рассеяния.
Чтобы продемонстрировать это, мы будем использовать набор данных diamonds. Чтобы следовать коду, откройте скрипт bda / part2 / charts / 03_multivariate_analysis.R .
library(ggplot2)
data(diamonds)
# Correlation matrix plots
keep_vars = c('carat', 'depth', 'price', 'table')
df = diamonds[, keep_vars]
# compute the correlation matrix
M_cor = cor(df)
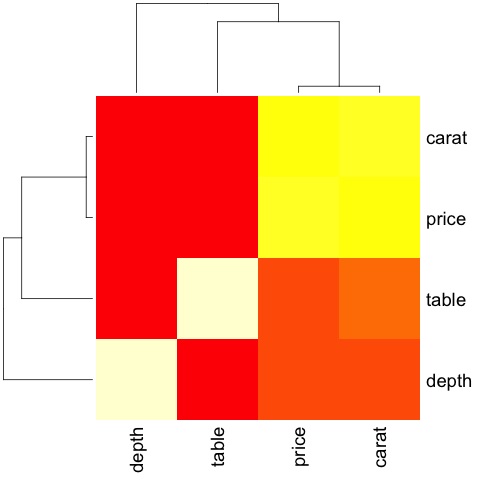
# carat depth price table
# carat 1.00000000 0.02822431 0.9215913 0.1816175
# depth 0.02822431 1.00000000 -0.0106474 -0.2957785
# price 0.92159130 -0.01064740 1.0000000 0.1271339
# table 0.18161755 -0.29577852 0.1271339 1.0000000
# plots
heat-map(M_cor)
Код выдаст следующий вывод —
Это резюме, оно говорит нам, что существует сильная корреляция между ценой и каретой, и не так много среди других переменных.
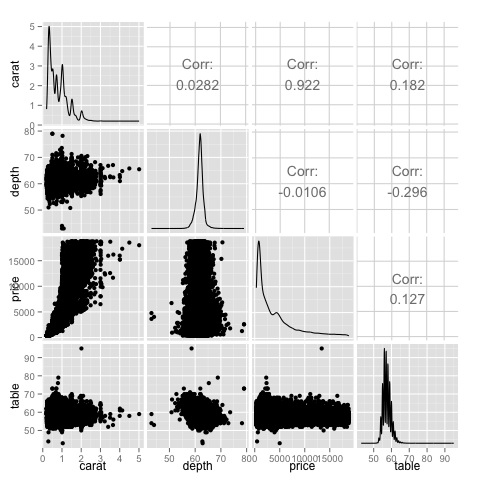
Корреляционная матрица может быть полезна, когда у нас есть большое количество переменных, и в этом случае построение исходных данных будет нецелесообразным. Как уже упоминалось, можно показать необработанные данные также —
library(GGally) ggpairs(df)
На графике видно, что результаты, отображаемые на тепловой карте, подтверждены, между ценовой и каратной переменными есть корреляция 0,922.
Это отношение можно визуализировать на диаграмме рассеяния цена-карат, расположенной в (3, 1) индексе матрицы рассеяния.