Временной ряд — это последовательность наблюдений категориальных или числовых переменных, проиндексированных по дате или метке времени. Ярким примером данных временных рядов является временной ряд цены акций. В следующей таблице мы видим основную структуру данных временных рядов. В этом случае наблюдения записываются каждый час.
| Отметка | Сток — Цена |
|---|---|
| 2015-10-11 09:00:00 | 100 |
| 2015-10-11 10:00:00 | 110 |
| 2015-10-11 11:00:00 | 105 |
| 2015-10-11 12:00:00 | 90 |
| 2015-10-11 13:00:00 | 120 |
Обычно первым шагом в анализе временных рядов является построение ряда, это обычно делается с помощью линейного графика.
Наиболее распространенным применением анализа временных рядов является прогнозирование будущих значений числового значения с использованием временной структуры данных. Это означает, что имеющиеся наблюдения используются для прогнозирования значений из будущего.
Временное упорядочение данных подразумевает, что традиционные методы регрессии бесполезны. Чтобы построить надежный прогноз, нам нужны модели, которые учитывают временное упорядочение данных.
Наиболее широко используемая модель для анализа временных рядов называется авторегрессионной скользящей средней (ARMA). Модель состоит из двух частей: авторегрессионной (AR) и скользящей средней (MA). Затем модель обычно называют моделью ARMA (p, q), где p — порядок авторегрессионной части, а q — порядок скользящей средней.
Авторегрессионная модель
AR (p) читается как авторегрессионная модель порядка p. Математически это записывается как —
Xt=c+ sumPi=1 phiiXt−i+ varepsilont
где {φ 1 ,…, φ p } — параметры, подлежащие оценке, c — постоянная величина, а случайная величина ε t представляет белый шум. Некоторые ограничения необходимы для значений параметров, чтобы модель оставалась стационарной.
Скользящая средняя
Обозначение MA (q) относится к модели скользящего среднего порядка q —
Xt= mu+ varepsilont+ sumqi=1 thetai varepsilont−i
где θ 1 , …, θ q — параметры модели, μ — ожидание X t , а ε t , ε t — 1 , … — члены ошибки белого шума.
Авторегрессивная скользящая средняя
Модель ARMA (p, q) объединяет p членов авторегрессии и q членов скользящего среднего. Математически модель выражается следующей формулой:
Xt=c+ varepsilont+ sumPi=1 phiiXt−1+ sumqi=1 thetai varepsilonti
Мы видим, что модель ARMA (p, q) представляет собой комбинацию моделей AR (p) и MA (q) .
Чтобы дать некоторую интуицию модели, рассмотрим, что AR-часть уравнения стремится оценить параметры для наблюдений X t — i , чтобы предсказать значение переменной в X t . В конце концов, это средневзвешенное значение прошлых значений. Раздел MA использует тот же подход, но с ошибкой предыдущих наблюдений, ε t — i . Таким образом, в итоге результат модели является средневзвешенным.
Следующий фрагмент кода демонстрирует, как реализовать ARMA (p, q) в R.
# install.packages("forecast")
library("forecast")
# Read the data
data = scan('fancy.dat')
ts_data <- ts(data, frequency = 12, start = c(1987,1))
ts_data
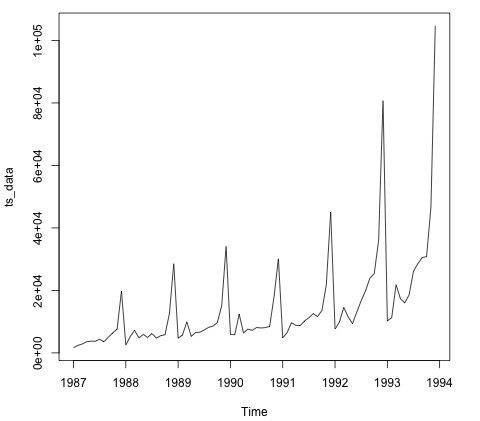
plot.ts(ts_data)
Построение данных обычно является первым шагом, чтобы выяснить, есть ли временная структура в данных. Из сюжета видно, что в конце каждого года наблюдаются сильные всплески.
Следующий код соответствует модели ARMA для данных. Он запускает несколько комбинаций моделей и выбирает ту, в которой меньше ошибок.