В области математики и информатики теория графов — это изучение графов, связанных с отношениями между ребрами и вершинами . Это популярный предмет, имеющий свои приложения в компьютерных науках, информационных технологиях, бионауках, математике и лингвистике. Без дальнейших церемоний, давайте начнем с определения графа.
Что такое график?
Граф представляет собой графическое представление набора объектов, где некоторые пары объектов связаны ссылками. Взаимосвязанные объекты представлены точками, называемыми вершинами, а связи, соединяющие вершины, называются ребрами .
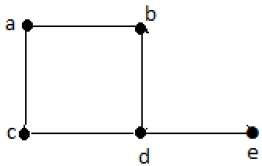
Формально граф представляет собой пару множеств (V, E), где V — множество вершин, а E — множество ребер, соединяющих пары вершин. Посмотрите на следующий график —
На приведенном выше графике
V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de}
Приложения теории графов
Теория графов имеет свои приложения в различных областях техники —
Электротехника — понятия теории графов широко используются при проектировании схемных соединений. Типы или организация соединений называются топологиями. Некоторыми примерами топологий являются топологии «звезда», «мост», «серия» и «параллельная топология».
Информатика — Теория графов используется для изучения алгоритмов. Например,
Компьютерная сеть — отношения между взаимосвязанными компьютерами в сети следуют принципам теории графов.
Наука . Молекулярная структура и химическая структура вещества, структура ДНК организма и т. Д. Представлены графами.
Лингвистика — дерево синтаксического анализа языка и грамматика языка использует графики.
Общее — Маршруты между городами могут быть представлены с помощью графиков. Отображение иерархической упорядоченной информации, такой как генеалогическое дерево, может использоваться в качестве особого типа графа, называемого деревом.