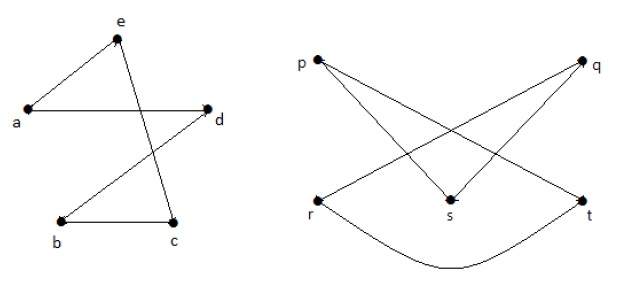
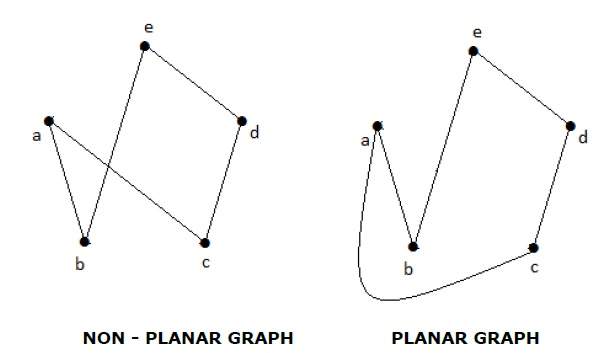
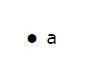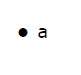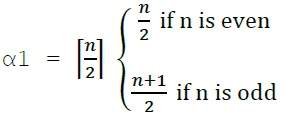Теория графов — Введение

В области математики и информатики теория графов — это изучение графов, связанных с отношениями между ребрами и вершинами . Это популярный предмет, имеющий свои приложения в компьютерных науках, информационных технологиях, бионауках, математике и лингвистике. Без дальнейших церемоний, давайте начнем с определения графа.

Что такое график?

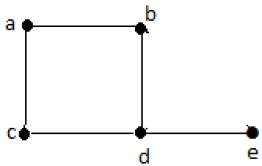
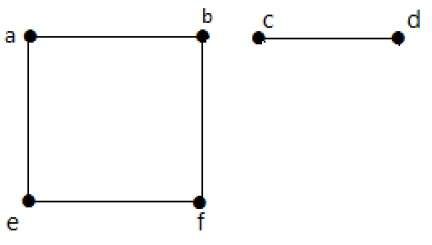
Граф представляет собой графическое представление набора объектов, где некоторые пары объектов связаны ссылками. Взаимосвязанные объекты представлены точками, называемыми вершинами, а связи, соединяющие вершины, называются ребрами .

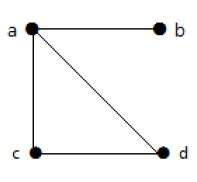
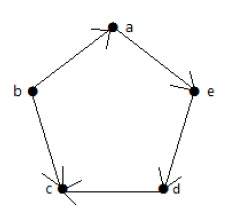
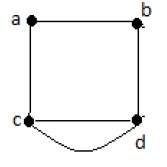
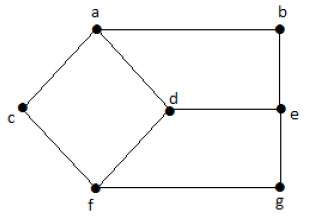
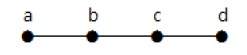
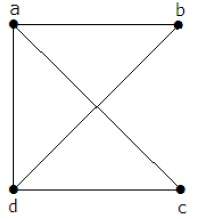
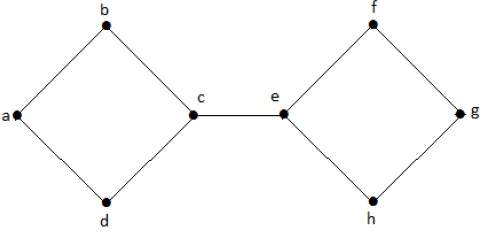
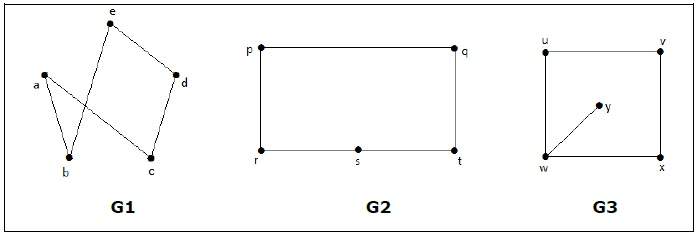
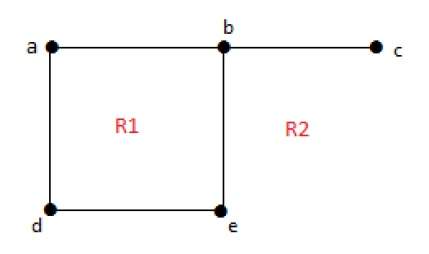
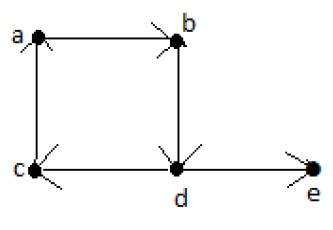
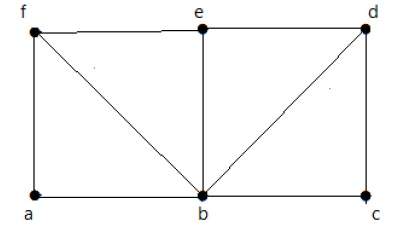
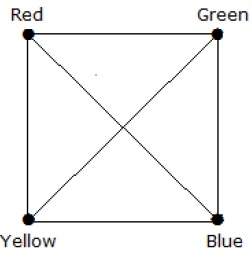
Формально граф представляет собой пару множеств (V, E), где V — множество вершин, а E — множество ребер, соединяющих пары вершин. Посмотрите на следующий график —

На приведенном выше графике

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

Приложения теории графов

Теория графов имеет свои приложения в различных областях техники —

• Электротехника — понятия теории графов широко используются при проектировании схемных соединений. Типы или организация соединений называются топологиями. Некоторыми примерами топологий являются топологии «звезда», «мост», «серия» и «параллельная топология».

• Информатика — Теория графов используется для изучения алгоритмов. Например,

  • Алгоритм Крускала
  • Алгоритм Прима
  • Алгоритм Дейкстры

• Компьютерная сеть — отношения между взаимосвязанными компьютерами в сети следуют принципам теории графов.

• Наука . Молекулярная структура и химическая структура вещества, структура ДНК организма и т. Д. Представлены графами.

• Лингвистика — дерево синтаксического анализа языка и грамматика языка использует графики.

• Общее — Маршруты между городами могут быть представлены с помощью графиков. Отображение иерархической упорядоченной информации, такой как генеалогическое дерево, может использоваться в качестве особого типа графа, называемого деревом.

Электротехника — понятия теории графов широко используются при проектировании схемных соединений. Типы или организация соединений называются топологиями. Некоторыми примерами топологий являются топологии «звезда», «мост», «серия» и «параллельная топология».

Информатика — Теория графов используется для изучения алгоритмов. Например,

Компьютерная сеть — отношения между взаимосвязанными компьютерами в сети следуют принципам теории графов.

Наука . Молекулярная структура и химическая структура вещества, структура ДНК организма и т. Д. Представлены графами.

Лингвистика — дерево синтаксического анализа языка и грамматика языка использует графики.

Общее — Маршруты между городами могут быть представлены с помощью графиков. Отображение иерархической упорядоченной информации, такой как генеалогическое дерево, может использоваться в качестве особого типа графа, называемого деревом.

Теория графов — основы

График — это диаграмма точек и линий, соединенных с точками. У него есть по крайней мере одна линия, соединяющая набор из двух вершин без вершин, соединяющих себя. Понятие графов в теории графов опирается на некоторые основные термины, такие как точка, линия, вершина, ребро, степень вершин, свойства графов и т. Д. Здесь, в этой главе, мы рассмотрим эти основы теории графов.

точка

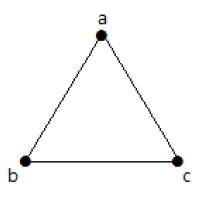
Точка — это конкретная позиция в одномерном, двухмерном или трехмерном пространстве. Для лучшего понимания точку можно обозначить алфавитом. Его можно обозначить точкой.

пример

Здесь точка — это точка с именем «а».

Линия

Линия — это связь между двумя точками. Это может быть представлено сплошной линией.

пример

Здесь «а» и «б» являются точками. Связь между этими двумя точками называется линией.

темя

Вершина — это точка, где встречаются несколько линий. Это также называется узлом . Подобно точкам, вершина также обозначается алфавитом.

пример

Здесь вершина названа с алфавитом «а».

край

Ребро — это математический термин для линии, соединяющей две вершины. Многие ребра могут быть сформированы из одной вершины. Без вершины ребро не может быть сформировано. Для ребра должна быть начальная и конечная вершина.

пример

Здесь «a» и «b» — две вершины, и связь между ними называется ребром.

график

Граф ‘G’ определяется как G = (V, E), где V — множество всех вершин, а E — множество всех ребер графа.

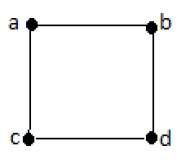
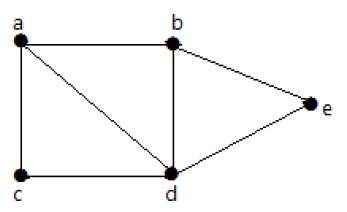
Пример 1

В приведенном выше примере ab, ac, cd и bd являются ребрами графа. Аналогично, a, b, c и d являются вершинами графа.

Пример 2

В этом графе есть четыре вершины a, b, c и d и четыре ребра ab, ac, ad и cd.

петля

В графе, если ребро нарисовано от вершины к себе, это называется циклом.

Пример 1

На приведенном выше графике V — вершина, для которой у нее есть ребро (V, V), образующее петлю.

Пример 2

В этом графе есть две петли, которые сформированы в вершине a, и вершине b.

Степень вершины

Это число вершин, смежных с вершиной V.

Обозначение — град (V).

В простом графе с n числом вершин степень любых вершин равна —

deg(v) ≤ n – 1 ∀ v ∈ G

Вершина может образовывать ребро со всеми остальными вершинами, кроме самой себя. Таким образом, степень вершины будет равна числу вершин в графе минус 1 . Это 1 для собственной вершины, поскольку она не может образовывать петлю сама по себе. Если в любой из вершин есть петля, то это не простой граф.

Степень вершины можно рассматривать по двум случаям графов —

• Ненаправленный граф
• Направленный граф

Степень вершины в неориентированном графе

Ненаправленный граф не имеет направленных ребер. Рассмотрим следующие примеры.

Пример 1

Посмотрите на следующий график —

На приведенном выше неориентированном графике

• deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.

• deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.

• deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро

  Итак, «c» — это вершина с кулоном .

• deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.

• deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.

  Так что «е» — изолированная вершина .

deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.

deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.

deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро

Итак, «c» — это вершина с кулоном .

deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.

deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.

Так что «е» — изолированная вершина .

Пример 2

Посмотрите на следующий график —

На приведенном выше графике

deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2 и deg (e) = 0.

Вершина «е» является изолированной вершиной. Граф не имеет никакой вершины.

Степень вершины в ориентированном графе

В ориентированном графе каждая вершина имеет степень и степень.

Степень графа

• Степень вершины V — это количество ребер, входящих в вершину V.

• Обозначение — град ^— (V).

Степень вершины V — это количество ребер, входящих в вершину V.

Обозначение — град ^— (V).

Степень графа

• Отступ вершины V — это число ребер, выходящих из вершины V.

• Обозначение — град ⁺ (V).

Отступ вершины V — это число ребер, выходящих из вершины V.

Обозначение — град ⁺ (V).

Рассмотрим следующие примеры.

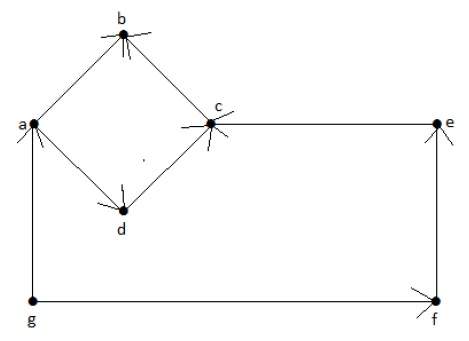
Пример 1

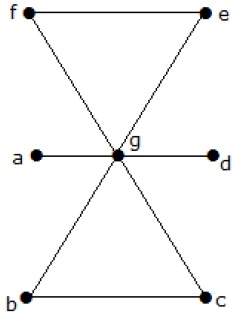
Посмотрите на следующий ориентированный граф. Вершина «а» имеет два ребра, «ad» и «ab», которые идут наружу. Следовательно, его степень равна 2. Аналогично, существует ребро «ga», идущее к вершине «a». Следовательно, степень «а» равна 1.

Степень и степень других вершин показаны в следующей таблице:

темя	полустепень захода	полустепень
	1	2
б	2	0
с	2	1
d	1	1
е	1	1
е	1	1
г	0	2

Пример 2

Посмотрите на следующий ориентированный граф. Вершина ‘a’ имеет ребро ‘ae’, идущее наружу от вершины ‘a’. Следовательно, его степень равна 1. Аналогично, у графа есть ребро «ba», приближающееся к вершине «a». Следовательно, степень «а» равна 1.

Степень и степень других вершин показаны в следующей таблице:

темя	полустепень захода	полустепень
	1	1
б	0	2
с	2	0
d	1	1
е	1	1

Кулон Вертекс

Используя степень вершины, мы получаем два специальных типа вершин. Вершина с первой степенью называется нерешенной вершиной.

пример

Здесь, в этом примере, вершина ‘a’ и вершина ‘b’ имеют соединенное ребро ‘ab’. Таким образом, что касается вершины «a», то к вершине «b» имеется только одно ребро, и аналогично по отношению к вершине «b» есть только одно ребро к вершине «a». Наконец, вершина ‘a’ и вершина ‘b’ имеют степень как единицу, которая также называется висячей вершиной.

Изолированная вершина

Вершина с нулевой степенью называется изолированной вершиной.

пример

Здесь вершина «a» и вершина «b» не имеют связи между собой, а также с любыми другими вершинами. Таким образом, степень обеих вершин ‘a’ и ‘b’ равна нулю. Они также называются изолированными вершинами.

смежность

Вот нормы смежности —

• В графе две вершины называются смежными, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается одним ребром, соединяющим эти две вершины.

• В графе два ребра называются смежными, если между двумя ребрами есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.

В графе две вершины называются смежными, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается одним ребром, соединяющим эти две вершины.

В графе два ребра называются смежными, если между двумя ребрами есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.

Пример 1

На приведенном выше графике —

• «a» и «b» — это смежные вершины, так как между ними есть общее ребро «ab».

• «a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».

• ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.

• be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.

«a» и «b» — это смежные вершины, так как между ними есть общее ребро «ab».

«a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».

ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.

be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.

Пример 2

На приведенном выше графике —

• a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.

• ‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.

• ‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.

• ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.

a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.

‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.

‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.

ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.

Параллельные края

В графе, если пара вершин соединена более чем одним ребром, то эти ребра называются параллельными ребрами.

На приведенном выше графике «a» и «b» — это две вершины, которые соединены между собой двумя ребрами «ab» и «ab». Так это называется параллельным ребром.

Мульти График

Граф, имеющий параллельные ребра, называется мультиграфом.

Пример 1

На приведенном выше графике есть пять ребер «ab», «ac», «cd», «cd» и «bd». Поскольку ‘c’ и ‘d’ имеют два параллельных ребра между ними, это мультиграф.

Пример 2

На приведенном выше графике вершины «b» и «c» имеют два ребра. Вершины ‘e’ и ‘d’ также имеют два ребра между ними. Следовательно, это мультиграф.

Степень последовательности графика

Если степени всех вершин в графе расположены в порядке убывания или возрастания, то полученная последовательность называется последовательностью графа графа.

Пример 1

темя		б	с	d	е
Присоединенный к	До нашей эры	объявление	объявление	с, Ь, е	d
степень	2	2	2	3	1

На приведенном выше графике для вершин {d, a, b, c, e} последовательность степеней равна {3, 2, 2, 2, 1}.

Пример 2

темя		б	с	d	е	е
Присоединенный к	быть	а, с	б, г	с, е	объявление	—
степень	2	2	2	2	2	0

На приведенном выше графике для вершин {a, b, c, d, e, f} последовательность степеней равна {2, 2, 2, 2, 2, 0}.

Теория графов — Основные свойства

Графы имеют различные свойства, которые используются для характеристики графов в зависимости от их структуры. Эти свойства определены в конкретных терминах, относящихся к области теории графов. В этой главе мы обсудим несколько основных свойств, которые являются общими для всех графиков.

Расстояние между двумя вершинами

Это число ребер в кратчайшем пути между вершиной U и вершиной V. Если существует несколько путей, соединяющих две вершины, то кратчайший путь рассматривается как расстояние между двумя вершинами.

Обозначение — d (U, V)

Может быть любое количество путей из одной вершины в другую. Среди них вам нужно выбрать только самый короткий.

пример

Посмотрите на следующий график —

Здесь расстояние от вершины ‘d’ до вершины ‘e’ или просто ‘de’ равно 1, поскольку между ними есть одно ребро. Существует много путей от вершины ‘d’ до вершины ‘e’ —

• да, а, бе
• дф, фг, гэ
• де (считается для расстояния между вершинами)
• дф, фц, ca, ab, be
• да, ac, cf, fg, ge

Эксцентриситет вершины

Максимальное расстояние между вершиной и всеми остальными вершинами рассматривается как эксцентриситет вершины.

Обозначение — e (V)

Расстояние от конкретной вершины до всех других вершин графа берется, и среди этих расстояний эксцентриситет является наибольшим из расстояний.

пример

На приведенном выше графике эксцентриситет «а» равен 3.

Расстояние от «a» до «b» равно 1 («ab»),

от ‘a’ до ‘c’ равно 1 (‘ac’),

от «а» до «d» равно 1 («объявление»),

от ‘a’ до ‘e’ равно 2 (‘ab’ — ‘be’) или (‘ad’ — ‘de’),

от ‘a’ до ‘f’ равно 2 (‘ac’ — ‘cf’) или (‘ad’ — ‘df’),

от ‘a’ до ‘g’ равно 3 (‘ac’ — ‘cf’ — ‘fg’) или (‘ad’ — ‘df’ — ‘fg’).

Таким образом, эксцентриситет равен 3, что является максимумом от вершины «а» от расстояния между «ag», которое является максимальным.

Другими словами,

е (б) = 3

е (с) = 3

е (д) = 2

е (е) = 3

е (е) = 3

е (г) = 3

Радиус связного графа

Минимальный эксцентриситет от всех вершин рассматривается как радиус графа G. Минимальный среди всех максимальных расстояний между вершиной до всех остальных вершин рассматривается как радиус графа G.

Обозначение — r (G)

Из всех эксцентриситетов вершин графа радиус связного графа является минимумом всех этих эксцентриситетов.

Пример — На приведенном выше графике r (G) = 2, что является минимальным эксцентриситетом для «d».

Диаметр графика

Максимальный эксцентриситет от всех вершин рассматривается как диаметр графа G. Максимальный из всех расстояний между вершиной до всех других вершин рассматривается как диаметр графа G.

Обозначение — d (G)

Из всех эксцентриситетов вершин графа диаметр связного графа является максимальным из всех этих эксцентриситетов.

Пример. На приведенном выше графике d (G) = 3; что является максимальным эксцентриситетом.

Центральная точка

Если эксцентриситет графа равен его радиусу, то он называется центральной точкой графа. Если

e (V) = r (V),

тогда «V» является центральной точкой графа «G».

Пример — в примере графика ‘d’ является центральной точкой графика.

e (d) = r (d) = 2

Центр

Множество всех центральных точек «G» называется центром графа.

Пример. В примере графика {‘d’} является центром графика.

Длина окружности

Число ребер в самом длинном цикле «G» называется окружностью «G».

Пример. На графике примера длина окружности равна 6, что мы получили из самого длинного цикла acfgeba или acfdeba.

обхват

Число ребер в кратчайшем цикле G называется его обхват.

Обозначения — g (G).

Пример — в примере графика обхват графа равен 4, который мы получили из кратчайшего цикла acfda или dfged или abeda.

Теорема о сумме степеней вершин

Если G = (V, E) ненаправленный граф с вершинами V = {V ₁ , V ₂ ,… V _n }, то

Следствие 1

Если G = (V, E) ориентированный граф с вершинами V = {V ₁ , V ₂ ,… V _n }, то

Следствие 2

В любом неориентированном графе число вершин с нечетной степенью является четным.

Следствие 3

В неориентированном графе, если степень каждой вершины равна k, то

к | V | = 2 | E |

Следствие 4

В неориентированном графе, если степень каждой вершины не меньше k, то

к | V | ≤ 2 | E |

Следствие 5

В неориентированном графе, если степень каждой вершины не более k, то

к | V | ≥ 2 | E |

Теория графов — Типы графов

Существуют различные типы графиков в зависимости от количества вершин, количества ребер, взаимосвязанности и их общей структуры. Мы обсудим только несколько важных типов графиков в этой главе.

Нулевой график

Граф, не имеющий ребер , называется нулевым графом .

пример

На приведенном выше графике есть три вершины с именами «a», «b» и «c», но среди них нет ребер. Следовательно, это нулевой граф.

Тривиальный график

Граф с единственной вершиной называется тривиальным графом .

пример

На приведенном выше графике есть только одна вершина «а» без других ребер. Следовательно, это тривиальный граф.

Ненаправленный граф

Ненаправленный граф содержит ребра, но ребра не являются ориентированными.

пример

В этом графе «a», «b», «c», «d», «e», «f», «g» — вершины, а «ab», «bc», «cd», «da». ‘,’ ag ‘,’ gf ‘,’ ef ‘- ребра графа. Поскольку это ненаправленный граф, ребра «ab» и «ba» совпадают. Точно так же другие ребра также рассматриваются аналогичным образом.

Направленный граф

В ориентированном графе каждое ребро имеет направление.

пример

На приведенном выше графике у нас есть семь вершин «a», «b», «c», «d», «e», «f» и «g», и восемь ребер «ab», «cb», « dc ‘,’ ad ‘,’ ec ‘,’ fe ‘,’ gf ‘и’ ga ‘. Поскольку это ориентированный граф, на каждом ребре есть метка стрелки, показывающая его направление. Обратите внимание, что в ориентированном графе «ab» отличается от «ba».

Простой график

Граф без петель и параллельных ребер называется простым графом.

• Максимально возможное число ребер в одном графе с n вершинами равно ⁿ C _2, где ⁿ C ₂ = n (n — 1) / 2.

• Число простых графов возможно с n вершинами = 2 ^{n c ₂} = 2 ^{n (n-1) / 2} .

Максимально возможное число ребер в одном графе с n вершинами равно ⁿ C _2, где ⁿ C ₂ = n (n — 1) / 2.

Число простых графов возможно с n вершинами = 2 ^{n c ₂} = 2 ^{n (n-1) / 2} .

пример

На следующем графике есть 3 вершины с 3 ребрами, которые являются максимальными, исключая параллельные ребра и петли. Это можно доказать с помощью приведенных выше формул.

Максимальное количество ребер с n = 3 вершинами —

n C 2 = n(n–1)/2
   = 3(3–1)/2
   = 6/2
   = 3 edges

Максимальное количество простых графов с n = 3 вершинами —

2 n C 2 = 2 n(n-1)/2
   = 2 3(3-1)/2
   = 2 3
   = 8

Эти 8 графиков, как показано ниже —

Связанный график

Граф G называется связным, если между каждой парой вершин существует путь . Для каждой вершины графа должно быть хотя бы одно ребро. Так что мы можем сказать, что он связан с какой-то другой вершиной на другой стороне ребра.

пример

На следующем графике каждая вершина имеет свое ребро, соединенное с другим ребром. Следовательно, это связный граф.

Отключенный график

Граф G несвязен, если он не содержит хотя бы двух связанных вершин.

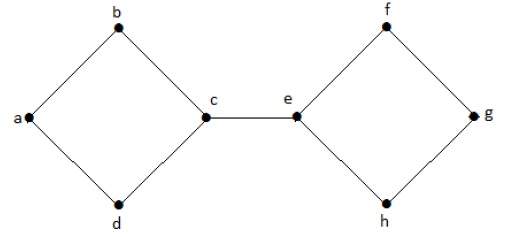
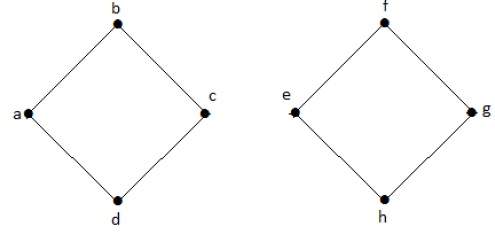
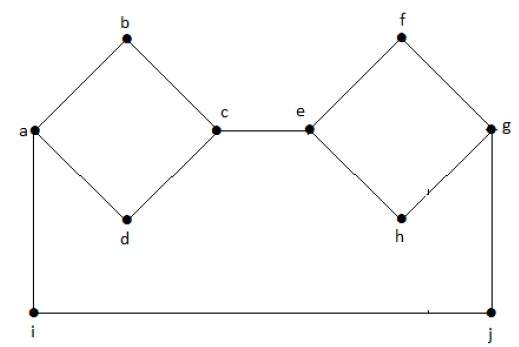
Пример 1

Следующий график является примером отключенного графа, где есть два компонента, один с вершинами «a», «b», «c», «d», а другой с «e», «f», «g», ‘h’ вершины.

Два компонента независимы и не связаны друг с другом. Следовательно, он называется несвязным графом.

Пример 2

В этом примере есть два независимых компонента, abfe и cd, которые не связаны друг с другом. Следовательно, это несвязный граф.

Обычный график

Граф G называется регулярным, если все его вершины имеют одинаковую степень . В графе, если степень каждой вершины равна «k», то этот граф называется «k-регулярным графом».

пример

На следующих графиках все вершины имеют одинаковую степень. Поэтому эти графы называются регулярными графами.

В обоих графах все вершины имеют степень 2. Они называются 2-регулярными графами.

Полный график

Простой граф с «n» взаимными вершинами называется полным графом и обозначается «K _n » . В графе вершина должна иметь ребра со всеми остальными вершинами, тогда она называется полным графом.

Другими словами, если вершина связана со всеми остальными вершинами графа, то она называется полным графом.

пример

В следующих графах каждая вершина графа связана со всеми остальными вершинами графа, кроме самой себя.

На графике я

		б	с
	Нет соединения	Связано	Связано
б	Связано	Нет соединения	Связано
с	Связано	Связано	Нет соединения

На графике II

	п	Q	р	s
п	Нет соединения	Связано	Связано	Связано
Q	Связано	Нет соединения	Связано	Связано
р	Связано	Связано	Нет соединения	Связано
s	Связано	Связано	Связано	Нет соединения

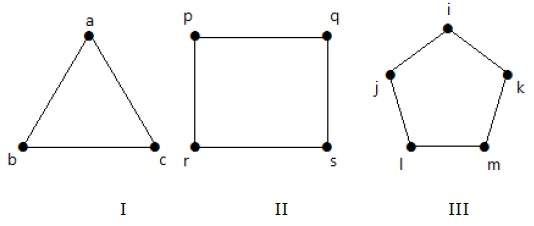
Цикл графика

Простой граф с n вершинами (n> = 3) и ребрами n называется графом циклов, если все его ребра образуют цикл длины n.

Если степень каждой вершины в графе равна двум, то она называется циклическим графом .

Обозначение — C _n

пример

Посмотрите на следующие графики —

• Граф I имеет 3 вершины с 3 ребрами, которые образуют цикл ‘ab-bc-ca’.

• Граф II имеет 4 вершины с 4 ребрами, которые образуют цикл ‘pq-qs-sr-rp’.

• Граф III имеет 5 вершин с 5 ребрами, которые образуют цикл ‘ik-km-ml-lj-ji’.

Граф I имеет 3 вершины с 3 ребрами, которые образуют цикл ‘ab-bc-ca’.

Граф II имеет 4 вершины с 4 ребрами, которые образуют цикл ‘pq-qs-sr-rp’.

Граф III имеет 5 вершин с 5 ребрами, которые образуют цикл ‘ik-km-ml-lj-ji’.

Следовательно, все данные графы являются графами циклов.

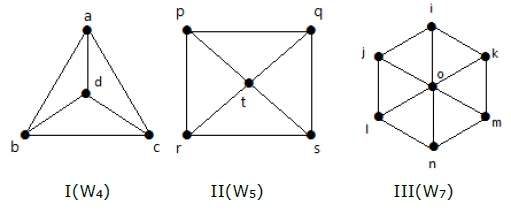
Колесо График

Граф колеса получается из графа циклов C _n-1 путем добавления новой вершины. Эта новая вершина называется Hub, которая связана со всеми вершинами C _n .

Обозначение — W _n

No. of edges in W n = No. of edges from hub to all other vertices +
                     No. of edges from all other nodes in cycle graph without a hub.
                     = (n–1) + (n–1)
                     = 2(n–1)

пример

Посмотрите на следующие графики. Они все колесные графики.

На графике I он получен из C ₃ путем добавления вершины в середине, названной ‘d’. Обозначается как W ₄ .

Number of edges in W 4 = 2(n-1) = 2(3) = 6

На графике II он получен из C ₄ путем добавления вершины в середине, названной ‘t’. Обозначается как W ₅ .

Number of edges in W 5 = 2(n-1) = 2(4) = 8

На графике III он получен из C ₆ путем добавления вершины в середине, названной ‘o’. Обозначается как W ₇ .

Number of edges in W 4 = 2(n-1) = 2(6) = 12

Циклический график

Граф с хотя бы одним циклом называется циклическим графом.

пример

В приведенном выше примере графа у нас есть два цикла abcda и cfgec. Следовательно, он называется циклическим графом.

Ациклический Граф

Граф без циклов называется ациклическим графом.

пример

В приведенном выше примере графа у нас нет циклов. Следовательно, это нециклический граф.

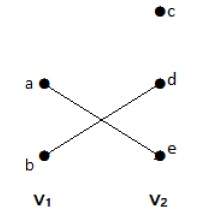
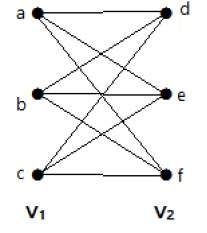
Двудольный график

Простой граф G = (V, E) с разбиением вершин V = {V ₁ , V ₂ } называется двудольным графом, если каждое ребро E соединяет вершину в V ₁ с вершиной в V ₂ .

В общем случае бипертитовый граф имеет два набора вершин, скажем, V ₁ и V ₂ , и если ребро нарисовано, он должен соединить любую вершину в наборе V ₁ с любой вершиной в наборе V ₂ .

пример

На этом графике вы можете наблюдать два набора вершин — V ₁ и V ₂ . Здесь два ребра с именами «ae» и «bd» соединяют вершины двух множеств V ₁ и V _2.

Полный двудольный график

Двудольный граф ‘G’, G = (V, E) с разбиением V = {V ₁ , V ₂ } называется полным двудольным графом, если каждая вершина в V ₁ соединена с каждой вершиной V ₂ .

В общем, полный двудольный граф соединяет каждую вершину из множества V ₁ с каждой вершиной из множества V ₂ .

пример

Следующий граф является полным двудольным графом, потому что у него есть ребра, соединяющие каждую вершину из множества V ₁ с каждой вершиной из множества V ₂ .

Если | V ₁ | = m и | V ₂ | = n, то полный двудольный граф обозначается через K _{m, n} .

• K _{m, n} имеет (m + n) вершин и (mn) ребер.

• K _{m, n} регулярный граф, если m = n.

K _{m, n} имеет (m + n) вершин и (mn) ребер.

K _{m, n} регулярный граф, если m = n.

В общем случае полный двудольный граф не является полным графом .

K _{m, n} полный граф, если m = n = 1.

Максимальное число ребер в двудольном графе с n вершинами

Если n = 10, k5, 5 = ⌊ n 2/4 ⌋ = ⌊ 10 2/4 ⌋ = 25

Аналогично К6, 4 = 24

К7, 3 = 21

К8, 2 = 16

К9, 1 = 9

Если n = 9, k5, 4 = ⌊ n 2/4 ⌋ = ⌊ 9 2/4 ⌋ = 20

Аналогично К6, 3 = 18

К7, 2 = 14

К8, 1 = 8

«G» является двудольным графом, если в «G» нет циклов нечетной длины. Частным случаем двудольного графа является звездный граф .

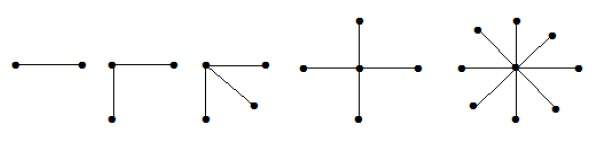
Звездный График

Полный двудольный граф вида K _{1, n-1} является графом звезд с n-вершинами. Звездный граф является полным двудольным графом, если одна вершина принадлежит одному набору, а все остальные вершины принадлежат другому набору.

пример

На приведенных выше графиках из n вершин все n – 1 вершины связаны с одной вершиной. Следовательно, оно имеет вид K _{1, n-1,} которые являются графами звезд.

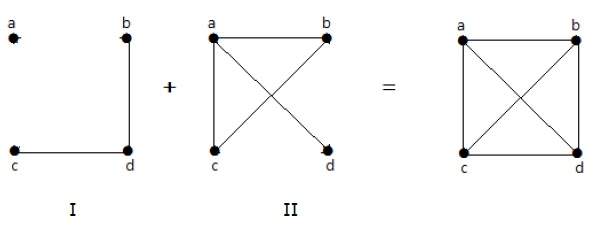
Дополнение графика

Пусть ‘ G — ‘ — простой граф с некоторыми вершинами, такими как у G, и ребро {U, V} присутствует в ‘ G — ‘ , если ребро отсутствует в G. Это означает, что две вершины смежны в « G — », если две вершины не смежны в G.

Если ребра, которые существуют в графе I, отсутствуют в другом графе II, и если граф I и граф II объединены вместе, чтобы сформировать полный граф, то граф I и граф II называются дополнениями друг друга.

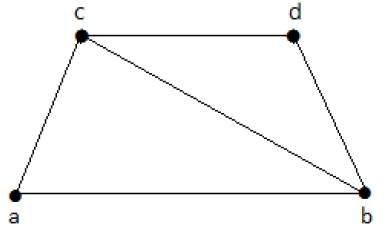
пример

В следующем примере graph-I имеет два ребра: «cd» и «bd». Его граф дополнения II имеет четыре ребра.

Обратите внимание, что ребра в графе-I отсутствуют в графе-II и наоборот. Следовательно, комбинация обоих графов дает полный граф из n вершин.

Примечание . Сочетание двух дополнительных графов дает полный граф.

Если «G» — простой граф, то

| E (G) | + | E ( ‘ G — ‘ ) | = | E (K _n ) |, где n = количество вершин в графе.

пример

Пусть ‘G’ — простой граф с девятью вершинами и двенадцатью ребрами, найдите число ребер в ‘ G — ‘ .

У вас есть, | E (G) | + | E ( ‘ G — ‘ ) | = | E (K _n ) |

12 + | E ( ‘ G — ‘ ) | знак равно

9 (9-1) / 2 = ⁹ C ₂

12 + | E ( ‘ G — ‘ ) | = 36

| E ( ‘ G — ‘ ) | = 24

«G» — простой граф с 40 ребрами, а его дополнение « G — » имеет 38 ребер. Найдите количество вершин в графе G или ‘ G — ‘ .

Пусть количество вершин в графе равно n.

Имеем, | E (G) | + | E ( ‘ G — ‘ ) | = | E (K _n ) |

40 + 38 = n (n-1) / 2

156 = n (n-1)

13 (12) = n (n-1)

n = 13

Теория графов — деревья

Деревья — это графики, которые не содержат ни одного цикла. Они представляют иерархическую структуру в графической форме. Деревья относятся к простейшему классу графов. Несмотря на их простоту, они имеют богатую структуру.

Деревья предоставляют целый ряд полезных приложений, от простого семейного дерева до сложных в структурах данных компьютерной науки.

дерево

Связный ациклический граф называется деревом. Другими словами, связный граф без циклов называется деревом.

Края дерева известны как ветви . Элементы деревьев называются их узлами . Узлы без дочерних узлов называются листовыми узлами .

Дерево с ‘n’ вершинами имеет ‘n-1’ ребер. Если у него есть еще одно ребро, превышающее ‘n-1’, то это дополнительное ребро, очевидно, должно соединиться с двумя вершинами, что приводит к образованию цикла. Затем он становится циклическим графом, что является нарушением для графа дерева.

Пример 1

График, показанный здесь, является деревом, потому что у него нет циклов, и он связан. Он имеет четыре вершины и три ребра, т. Е. Для ‘n’ вершин ‘n-1’ ребер, как указано в определении.

Примечание. Каждое дерево имеет как минимум две вершины первой степени.

Пример 2

В приведенном выше примере вершины «a» и «d» имеют степень один. А две другие вершины ‘b’ и ‘c’ имеют второй уровень. Это возможно, потому что для того, чтобы не формировать цикл, в диаграмме должно быть как минимум два отдельных ребра. Это не что иное, как два ребра со степенью один.

лес

Несвязный ациклический граф называется лесом. Другими словами, непересекающаяся коллекция деревьев называется лесом.

пример

Следующий график выглядит как два подграфа; но это один несвязный граф. На этом графике нет циклов. Отсюда ясно, что это лес.

Охватывающие деревья

Пусть G — связный граф, тогда подграф H в G называется остовным деревом в G, если —

• H это дерево
• H содержит все вершины G.

Остовное дерево T неориентированного графа G является подграфом, который включает в себя все вершины G.

пример

В приведенном выше примере G является связным графом, а H является подграфом G.

Ясно, что граф H не имеет циклов, это дерево с шестью ребрами, которое на единицу меньше общего числа вершин. Следовательно, H — остовное дерево группы G.

Circuit Rank

Пусть «G» связный граф с «n» вершинами и «m» ребрами. Остовное дерево ‘T’ группы G содержит (n-1) ребер.

Следовательно, количество ребер, которые нужно удалить из ‘G’, чтобы получить остовное дерево = m- (n-1), которое называется рангом схемы G.

Эта формула верна, потому что в остовном дереве вам нужно иметь ребра n-1. Из «m» ребер вам нужно сохранить «n – 1» ребер в графе.

Следовательно, удаление ребер n – 1 из m дает ребра, которые нужно удалить из графа, чтобы получить остовное дерево, которое не должно образовывать цикл.

пример

Посмотрите на следующий график —

Для графика, приведенного в примере выше, у вас есть m = 7 ребер и n = 5 вершин.

Тогда ранг цепи

G = m – (n – 1)
  = 7 – (5 – 1)
  = 3

пример

Пусть ‘G’ — связный граф с шестью вершинами, а степень каждой вершины равна трем. Найдите звание цепи «G».

По сумме теоремы о степени вершин

6 × 3 = 2 | E |

| E | = 9

Схема ранг = | E | — (| V | — 1)

= 9 — (6 — 1) = 4

Теорема Кирхгофа

Теорема Кирхгофа полезна для нахождения числа связующих деревьев, которые могут быть сформированы из связного графа.

пример

Матрица «А» заполняется так, как если между двумя вершинами есть ребро, то она должна быть задана как «1», иначе «0».

Теория графов — связность

Возможен ли переход графа из одной вершины в другую, определяется тем, как граф связан. Связность является основной концепцией в теории графов. Связность определяет, подключен ли график или нет. Он имеет подтемы, основанные на ребре и вершине, известные как связность ребер и вершин. Давайте обсудим их подробно.

связь

Граф называется связным, если между каждой парой вершин есть путь . От каждой вершины к любой другой вершине должен быть некоторый путь для прохождения. Это называется связностью графа. Граф с несколькими несвязанными вершинами и ребрами называется несвязным.

Пример 1

На следующем графике можно перейти от одной вершины к любой другой вершине. Например, можно перейти от вершины «а» к вершине «е», используя путь «ab-e».

Пример 2

В следующем примере переход от вершины ‘a’ к вершине ‘f’ невозможен, поскольку между ними нет прямого или косвенного пути. Следовательно, это несвязный граф.

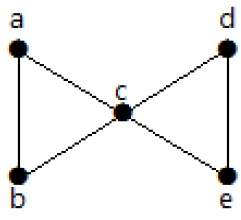
Cut Vertex

Пусть ‘G’ связный граф. Вершина V ∈ G называется разрезанной вершиной из «G», если «G-V» (исключить «V» из «G») приводит к несвязному графу. Удаление вырезанной вершины из графа разбивает ее на два или более графа.

Примечание. Удаление обрезанной вершины может привести к отключению графа.

Связный граф ‘G’ может иметь не более (n – 2) вершин среза.

пример

На следующем графике вершины ‘e’ и ‘c’ являются вырезанными вершинами.

Удалив «е» или «с», граф станет несвязным графом.

Без ‘g’ нет пути между вершиной ‘c’ и вершиной ‘h’ и многими другими. Следовательно, это несвязный граф с разрезанной вершиной в виде «е». Точно так же ‘c’ также является вершиной разреза для приведенного выше графа.

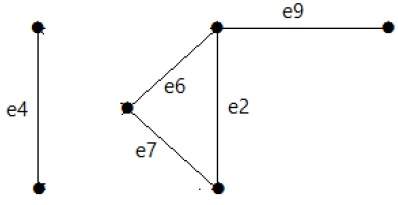
Cut Edge (Мост)

Пусть ‘G’ связный граф. Ребро «e» ∈ G называется отрезанным ребром, если «G-e» приводит к несвязному графу.

Если удаление ребра в графе приводит к двум или более графам, то это ребро называется Cut Edge.

пример

На следующем графике край обрезки равен [(c, e)]

Удаляя ребро (c, e) из графа, он становится несвязным графом.

В приведенном выше графике удаление ребра (c, e) разбивает граф на два, что является ничем иным, как несвязным графом. Следовательно, ребро (c, e) является отрезанным ребром графа.

Примечание. Пусть «G» — связный граф с «n» вершинами, тогда

• отрезок e ∈ G тогда и только тогда, когда ребро «e» не является частью какого-либо цикла в G.

• Максимально возможное количество режущих кромок равно n-1.

• всякий раз, когда существуют ребра среза, вершины среза также существуют, потому что по крайней мере одна вершина среза является вершиной среза.

• если вершина разреза существует, то край разреза может существовать или не существовать.

отрезок e ∈ G тогда и только тогда, когда ребро «e» не является частью какого-либо цикла в G.

Максимально возможное количество режущих кромок равно n-1.

всякий раз, когда существуют ребра среза, вершины среза также существуют, потому что по крайней мере одна вершина среза является вершиной среза.

если вершина разреза существует, то край разреза может существовать или не существовать.

Вырезать набор графика

Пусть ‘G’ = (V, E) связный граф. Подмножество E ‘E называется нарезанным множеством G, если удаление всех ребер E’ из G приводит к разъединению G.

Если удаление определенного числа ребер из графа делает его отключенным, то эти удаленные ребра называются набором вырезов графа.

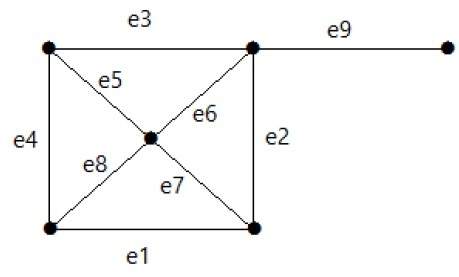
пример

Посмотрите на следующий график. Его набор срезов E1 = {e1, e3, e5, e8}.

После удаления набора вырезок E1 из графика это будет выглядеть следующим образом:

Точно так же есть другие наборы разрезов, которые могут отключить график —

• E3 = {e9} — наименьший набор вырезов графа.
• E4 = {e3, e4, e5}

Edge Connectivity

Пусть ‘G’ связный граф. Минимальное количество ребер, удаление которых приводит к отключению G, называется связностью ребер G.

Обозначение — λ (G)

Другими словами, число ребер в наименьшем отрезке G называется связностью ребер G.

Если «G» имеет ребро среза, то λ (G) равно 1. (связность ребра G.)

пример

Посмотрите на следующий график. Удаляя два минимальных ребра, связный граф становится несвязным. Следовательно, его краевая связность (λ (G)) равна 2.

Вот четыре способа отключить график, удалив два ребра:

Vertex Connectivity

Пусть ‘G’ связный граф. Минимальное количество вершин, удаление которых делает «G» либо несвязным, либо сокращает «G» до тривиального графа, называется связностью его вершин.

Обозначение — K (G)

пример

В приведенном выше графике удаление вершин ‘e’ и ‘i’ делает граф отключенным.

Если G имеет вырезанную вершину, то K (G) = 1.

Обозначение — Для любого связного графа G,

K (G) ≤ λ (G) ≤ δ (G)

Связность вершин (K (G)), связность ребер (λ (G)), минимальное количество градусов G (δ (G)).

пример

Вычислить λ (G) и K (G) для следующего графика —

Решение

Из графика

δ (G) = 3

K (G) ≤ λ (G) ≤ δ (G) = 3 (1)

K (G) ≥ 2 (2)

Удалив ребра {d, e} и {b, h}, мы можем отключить G.

Следовательно,

λ (G) = 2

2 ≤ λ (G) ≤ δ (G) = 2 (3)

Из (2) и (3) связность вершин K (G) = 2

Теория графов — Покрытия

Покрывающий граф — это подграф, который содержит либо все вершины, либо все ребра, соответствующие некоторому другому графу. Подграф, который содержит все вершины, называется покрытием линии / ребра . Подграф, содержащий все ребра, называется покрытием вершин .

Линия покрытия

Пусть G = (V, E) — граф. Подмножество C (E) называется покрытием линий G, если каждая вершина G инцидентна хотя бы с одним ребром в C, т. Е.

deg (V) ≥ 1 ∀ V ∈ G

потому что каждая вершина связана с другой вершиной ребром. Следовательно, он имеет минимальную степень 1.

пример

Посмотрите на следующий график —

Его подграфы, имеющие покрытие строк:

C 1 = {{a, b}, {c, d}}
C 2 = {{a, d}, {b, c}}
C 3 = {{a, b}, {b, c}, {b, d}}
C 4 = {{a, b}, {b, c}, {c, d}}

Покрытие линии ‘G’ не существует тогда и только тогда, когда ‘G’ имеет изолированную вершину. Линейное покрытие графа с «n» вершинами имеет не менее ⌊ n / 2 ⌋ ребер.

Минимальная линия покрытия

Линия, покрывающая C графа G, называется минимальной, если никакое ребро не может быть удалено из C.

пример

На приведенном выше графике подграфы, имеющие покрытие строк, выглядят следующим образом:

C 1 = {{a, b}, {c, d}}
C 2 = {{a, d}, {b, c}}
C 3 = {{a, b}, {b, c}, {b, d}}
C 4 = {{a, b}, {b, c}, {c, d}}

Здесь C ₁ , C ₂ , C ₃ — минимальные покрытия строк, а C ₄ — не потому, что мы можем удалить {b, c}.

Минимальное покрытие линии

Это также известно как Наименьшее Минимальное Покрытие Линии . Минимальное покрытие линий с минимальным числом ребер называется минимальным покрытием линий в G. Число ребер в минимальном покрытии линии в «G» называется числом покрытия линии в «G» (α ₁ ).

пример

В приведенном выше примере C ₁ и C ₂ являются минимальным покрытием линий G и α ₁ = 2.

• Каждое линейное покрытие содержит минимальное линейное покрытие.

• Каждое покрытие строк не содержит минимального покрытия строк (C ₃ не содержит минимального покрытия линий.

• Ни одно минимальное покрытие строк не содержит циклов.

• Если линия, покрывающая «C», не содержит путей длиной 3 или более, то «C» — это минимальное покрытие линий, поскольку все компоненты «C» являются звездным графом и из звездного графа ни одно ребро не может быть удалено.

Каждое линейное покрытие содержит минимальное линейное покрытие.

Каждое покрытие строк не содержит минимального покрытия строк (C ₃ не содержит минимального покрытия линий.

Ни одно минимальное покрытие строк не содержит циклов.

Если линия, покрывающая «C», не содержит путей длиной 3 или более, то «C» — это минимальное покрытие линий, поскольку все компоненты «C» являются звездным графом и из звездного графа ни одно ребро не может быть удалено.

Покрытие вершин

Пусть ‘G’ = (V, E) — граф. Подмножество K из V называется покрытием вершин из ‘G’, если каждое ребро из ‘G’ инцидентно или покрыто вершиной в ‘K’.

пример

Посмотрите на следующий график —

Подграфы, которые могут быть получены из приведенного выше графика, следующие:

K 1 = {b, c}
K 2 = {a, b, c}
K 3 = {b, c, d}
K 4 = {a, d}

Здесь K ₁ , K ₂ и K ₃ имеют покрытие вершин, тогда как K ₄ не имеет покрытия вершин, поскольку оно не покрывает ребро {bc}.

Минимальное покрытие вершин

Вершина «K» графа «G» называется минимальным покрытием вершин, если ни одна вершина не может быть удалена из «K».

пример

На приведенном выше графике подграфы, имеющие покрытие вершин, выглядят следующим образом:

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

Здесь K ₁ и K ₂ являются минимальными покрытиями вершин, тогда как в K ₃ вершина ‘d’ может быть удалена.

Минимальное покрытие вершин

Он также известен как наименьшее минимальное покрытие вершин. Минимальное покрытие вершин графа G с минимальным количеством вершин называется минимальным покрытием вершин.

Число вершин в минимальном покрытии вершин из G называется числом вершин, покрывающим G (α ₂ ).

пример

На следующем графике подграфы, имеющие покрытие вершин, выглядят следующим образом:

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

Здесь K ₁ — минимальное покрытие вершин G, поскольку оно имеет только две вершины. α ₂ = 2.

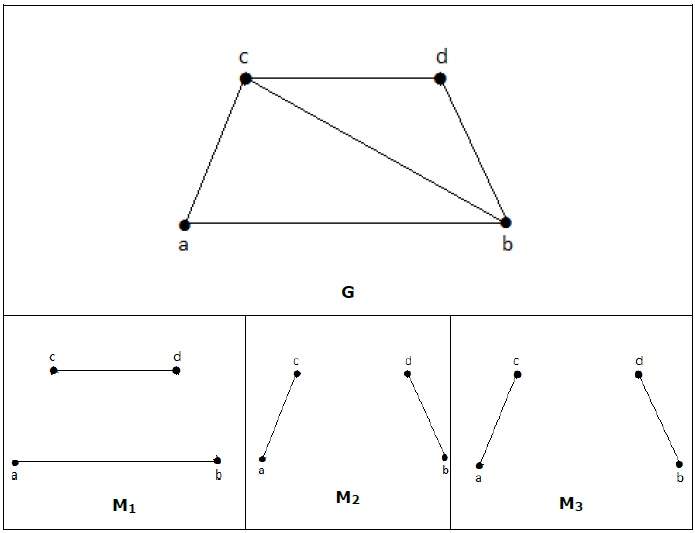
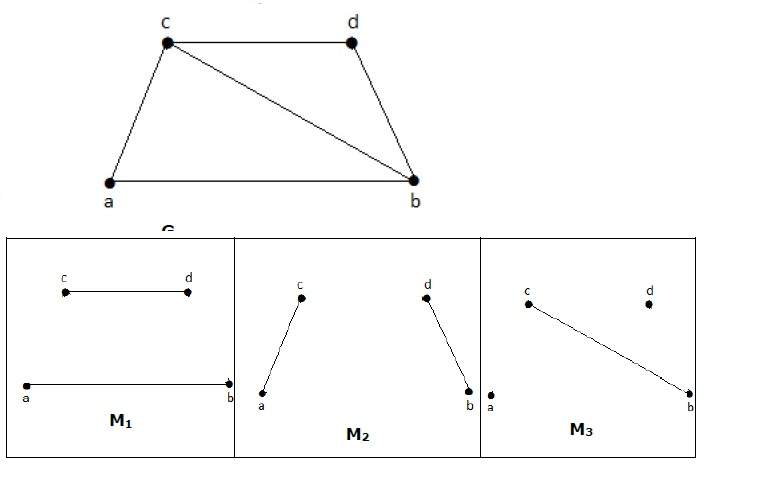
Теория графов — соответствия

Соответствующий граф — это подграф графа, в котором нет смежных ребер. Просто между двумя ребрами не должно быть общей вершины.

согласование

Пусть ‘G’ = (V, E) — граф. Подграф называется совпадающим M (G), если каждая вершина из G инцидентна не более чем с одним ребром в M, т. Е.

deg (V) ≤ 1 ∀ V ∈ G

это означает, что в совпадающем графе M (G) вершины должны иметь степень 1 или 0, где ребра должны падать от графа G.

Обозначение — M (G)

пример

В соответствии

если deg (V) = 1, то (V) называется соответствующим

если deg (V) = 0, то (V) не совпадает.

В сопоставлении нет двух соседних ребер. Это потому, что если любые два ребра смежны, то степень вершины, соединяющей эти два ребра, будет иметь степень 2, которая нарушает правило сопоставления.

Максимальное соответствие

Соответствующий M графа ‘G’ называется максимальным, если никакие другие ребра G не могут быть добавлены к M.

пример

M ₁ , M ₂ , M ₃ из приведенного выше графика — максимальное совпадение G.

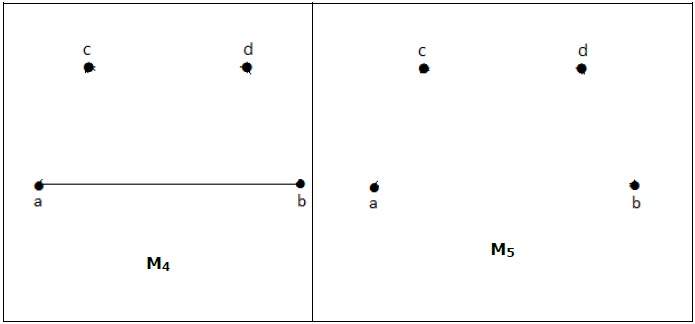
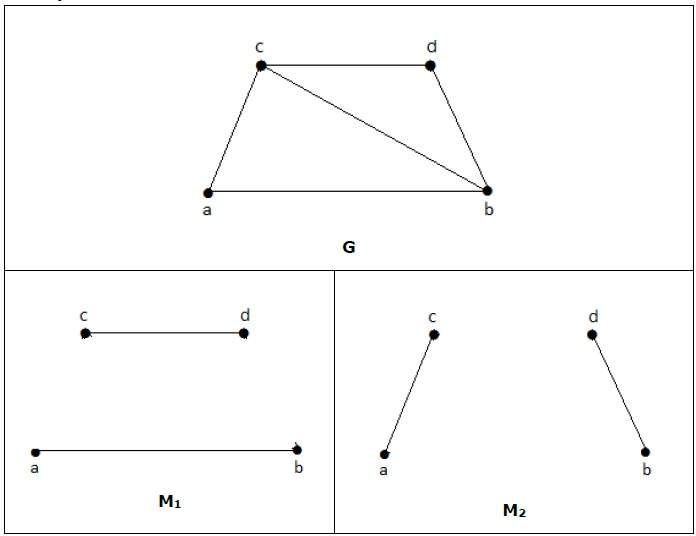
Максимальное соответствие

Это также известно как наибольшее максимальное соответствие. Максимальное соответствие определяется как максимальное соответствие с максимальным количеством ребер.

Число ребер в максимальном совпадении «G» называется его совпадающим номером .

пример

Для графа, приведенного в приведенном выше примере, M ₁ и M ₂ являются максимальным соответствием ‘G’, а его номер совпадения равен 2. Следовательно, используя граф G, мы можем сформировать только подграфы с максимум 2 ребрами. Следовательно, у нас есть совпадающее число как два.

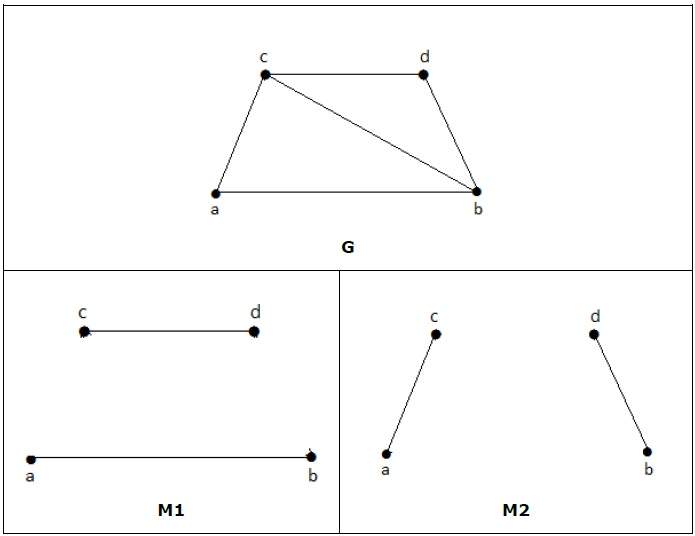
Идеальное соответствие

Сопоставление (M) графа (G) называется совершенным совпадением, если каждая вершина графа g (G) инцидентна ровно одному ребру совпадающего (M), т.е.

град (V) = 1 ∀ V

Степень каждой вершины в подграфе должна иметь степень 1.

пример

На следующих графиках M ₁ и M ₂ являются примерами идеального соответствия G.

Примечание. Каждое идеальное соответствие графа также является максимальным соответствием графа, поскольку нет шансов добавить еще одно ребро в графе идеального соответствия.

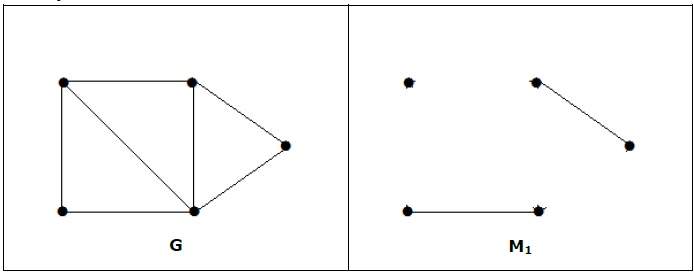
Максимальное соответствие графа не обязательно должно быть идеальным. Если граф «G» имеет идеальное совпадение, то число вершин | V (G) | даже. Если это нечетно, то последняя вершина соединяется с другой вершиной, и, наконец, остается одна вершина, которая не может быть спарена с любой другой вершиной, для которой степень равна нулю. Это явно нарушает принцип идеального соответствия.

пример

Примечание . Обратное утверждение выше не обязательно должно быть верным. Если G имеет четное число вершин, то M ₁ не обязательно должно быть совершенным.

пример

Это совпадение, но оно не является идеальным, даже если оно имеет четное количество вершин.

Теория графов — независимые множества

Независимые наборы представлены в наборах, в которых

• не должно быть никаких краев, смежных друг с другом . Между двумя ребрами не должно быть общей вершины.

• не должно быть никаких вершин, смежных друг с другом . Между любыми двумя вершинами не должно быть общего ребра.

не должно быть никаких краев, смежных друг с другом . Между двумя ребрами не должно быть общей вершины.

не должно быть никаких вершин, смежных друг с другом . Между любыми двумя вершинами не должно быть общего ребра.

Независимый набор линий

Пусть ‘G’ = (V, E) — граф. Подмножество L в E называется множеством независимых линий ‘G’, если нет двух ребер в L смежных. Такой набор называется набором независимых строк.

пример

Давайте рассмотрим следующие подмножества —

L 1 = {a,b}
L 2 = {a,b} {c,e}
L 3 = {a,d} {b,c}

В этом примере подмножества L ₂ и L ₃ явно не являются смежными ребрами в данном графе. Это независимые линейные наборы. Однако L ₁ не является независимым линейным набором, так как для создания независимого линейного набора должно быть как минимум два ребра.

Максимальный набор независимых линий

Независимый набор линий называется максимальным набором независимых линий графа «G», если никакое другое ребро «G» не может быть добавлено к «L».

пример

Давайте рассмотрим следующие подмножества —

L 1 = {a, b}
L 2 = {{b, e}, {c, f}}
L 3 = {{a, e}, {b, c}, {d, f}}
L 4 = {{a, b}, {c, f}}

L ₂ и L ₃ — максимальные независимые наборы линий / максимальное совпадение. Что касается только этих двух подмножеств, нет никакой возможности добавить любое другое ребро, которое не является смежным. Следовательно, эти два подмножества рассматриваются как максимальные независимые линейные множества.

Максимальный набор независимых линий

Максимальный набор независимых линий с максимальным числом ребер называется максимальным набором независимых линий с G.

Number of edges in a maximum independent line set of G (β 1 )
   = Line independent number of G
   = Matching number of G

пример

Давайте рассмотрим следующие подмножества —

L 1 = {a, b}
L 2 = {{b, e}, {c, f}}
L 3 = {{a, e}, {b, c}, {d, f}}
L 4 = {{a, b}, {c, f}}

L ₃ — это максимальное независимое линейное множество G с максимальными ребрами, которые не являются смежными ребрами в графе и обозначается как β ₁ = 3.

Примечание. Для любого графа G без изолированной вершины

α ₁ + β ₁ = количество вершин в графе = | V |

пример

Номер покрытия линии K _н / с _н / ш _н ,

Независимый от линии номер (соответствующий номер) = β ₁ = ⌊ n / 2 ⌋ α ₁ + β ₁ = n

Независимый набор вершин

Пусть ‘G’ = (V, E) — граф. Подмножество V называется независимым множеством G, если в S нет двух смежных вершин.

пример

Рассмотрим следующие подмножества из приведенных выше графиков —

S 1 = {e}
S 2 = {e, f}
S 3 = {a, g, c}
S 4 = {e, d}

Ясно, что S ₁ не является независимым множеством вершин, потому что для получения независимого множества вершин в графе должно быть как минимум две вершины. Но здесь это не тот случай. Подмножества S ₂ , S ₃ и S ₄ являются независимыми наборами вершин, потому что нет вершин, смежных с какой-либо одной вершиной из подмножеств.

Максимальный независимый набор вершин

Пусть ‘G’ граф, тогда независимое множество вершин из G называется максимальным, если никакая другая вершина из G не может быть добавлена ​​к ‘S’.

пример

Рассмотрим следующие подмножества из приведенных выше графиков.

S 1 = {e}
S 2 = {e, f}
S 3 = {a, g, c}
S 4 = {e, d}

S ₂ и S ₃ — максимальные независимые множества вершин группы ‘G’. В S ₁ и S ₄ мы можем добавить другие вершины; но в S ₂ и S ₃ мы не можем добавить любую другую вершину

Максимально независимый набор вершин

Максимальное независимое множество вершин из G с максимальным количеством вершин называется максимальным независимым множеством вершин.

пример

Рассмотрим следующие подмножества из приведенного выше графика —

S 1 = {e}
S 2 = {e, f}
S 3 = {a, g, c}
S 4 = {e, d}

Только S ₃ является максимальным независимым множеством вершин, поскольку оно охватывает наибольшее количество вершин. Количество вершин в максимальном независимом множестве вершин группы G называется независимым числом вершин группы G (β ₂ ).

пример

For the complete graph K n ,
      Vertex covering number = α 2 = n−1
      Vertex independent number = β 2 = 1
You have α 2 + β 2 = n
In a complete graph, each vertex is adjacent to its remaining (n − 1) vertices. Therefore, a maximum independent set of K n contains only one vertex.
Therefore,   β 2 =1
and          α 2 =|v| − β 2 = n-1

Примечание. Для любого графа «G» = (V, E)

• α ₂ + β ₂ = | v |

• Если ‘S’ является независимым множеством вершин ‘G’, то (V — S) является покрытием вершин G.

α ₂ + β ₂ = | v |

Если ‘S’ является независимым множеством вершин ‘G’, то (V — S) является покрытием вершин G.

Теория графов — раскраска

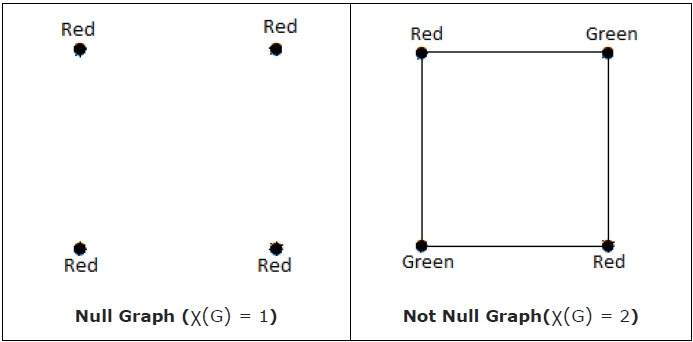
Раскраска графа — это не более чем простой способ маркировки компонентов графа, таких как вершины, ребра и области, при некоторых ограничениях. На графике нет двух смежных вершин, смежных ребер или смежных областей, окрашенных минимальным количеством цветов. Это число называется хроматическим числом, а граф называется правильно окрашенным графом .

Во время раскраски графа на графике устанавливаются следующие ограничения: цвета, порядок окраски, способ назначения цвета и т. Д. Раскраска присваивается вершине или конкретной области. Таким образом, вершины или области, имеющие одинаковые цвета, образуют независимые множества.

Окраска вершин

Раскраска вершин — это присвоение цветов вершинам графа G так, что никакие две смежные вершины не имеют одинакового цвета. Проще говоря, две вершины ребра не должны быть одного цвета.

Хроматическое число

Минимальное количество цветов, необходимое для раскраски вершин графа G, называется хроматическим числом G, обозначаемым X (G).

χ (G) = 1 тогда и только тогда, когда «G» является нулевым графом. Если ‘G’ не нулевой граф, то χ (G) ≥ 2

пример

Примечание . Граф ‘G’ называется n-покрываемым, если существует раскраска вершин, использующая не более n цветов, т. Е. X (G) ≤ n.

Окраска региона

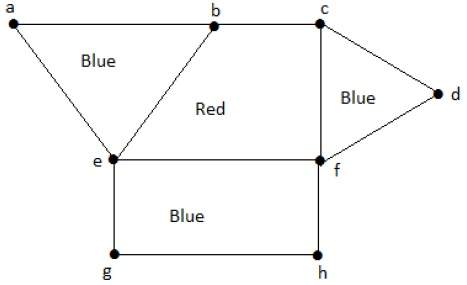
Раскраска областей — это присвоение цветов областям плоского графа, чтобы ни у двух соседних областей не было одинакового цвета. Говорят, что две области являются смежными, если они имеют общее ребро.

пример

Посмотрите на следующий график. Регионы ‘aeb’ и ‘befc’ являются смежными, поскольку между этими двумя регионами существует общая граница ‘be’.

Точно так же другие области также окрашены в зависимости от смежности. Этот график раскрашен следующим образом —

пример

Хроматическое число K _n равно

а) н

б) n – 1

в) ⌊ н / 2 ⌋

г) ⌈ н / 2 ⌉

Рассмотрим этот пример с K ₄ .

В полном графе каждая вершина смежна с остальными (n — 1) вершинами. Следовательно, каждая вершина требует нового цвета. Следовательно, хроматическое число K _n = n.

Приложения для раскраски графиков

Раскраска графа является одним из важнейших понятий в теории графов. Он используется во многих приложениях информатики в реальном времени, таких как —

• Кластеризация
• Сбор данных
• Захват изображения
• Сегментация изображения
• сетей
• Распределение ресурсов
• Планирование процессов

Теория графов — изоморфизм

Граф может существовать в разных формах, имеющих одинаковое количество вершин, ребер, а также одинаковую связность ребер. Такие графы называются изоморфными графами. Обратите внимание, что мы помечаем графики в этой главе главным образом для того, чтобы ссылаться на них и узнавать их друг от друга.

Изоморфные графы

Два графа G ₁ и G ₂ называются изоморфными, если —

• Их количество компонентов (вершин и ребер) одинаково.
• Их пограничное соединение сохраняется.

Примечание. Короче говоря, из двух изоморфных графов один является измененной версией другого. Немеченый граф также можно рассматривать как изоморфный граф.

There exists a function ‘f’ from vertices of G 1 to vertices of G 2
   [f: V(G 1 ) ⇒ V(G 2 )], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G 1 , then the 
   edge {f(U), f(V)} ∈ G 2 , then G 1 ≡ G 2 .

Заметка

Если G ₁ ≡ G _2, то —

• | V (G ₁ ) | = | V (G ₂ ) |

• | E (G ₁ ) | = | E (G ₂ ) |

• Степени последовательности G ₁ и G ₂ одинаковы.

• Если вершины {V ₁ , V ₂ , .. V _k } образуют цикл длины K в G ₁ , то вершины {f (V ₁ ), f (V ₂ ),… f (V _k )} должны сформироваться цикл длины K в G ₂ .

| V (G ₁ ) | = | V (G ₂ ) |

| E (G ₁ ) | = | E (G ₂ ) |

Степени последовательности G ₁ и G ₂ одинаковы.

Если вершины {V ₁ , V ₂ , .. V _k } образуют цикл длины K в G ₁ , то вершины {f (V ₁ ), f (V ₂ ),… f (V _k )} должны сформироваться цикл длины K в G ₂ .

Все вышеперечисленные условия необходимы для того, чтобы графы G ₁ и G ₂ были изоморфными, но не достаточными для доказательства того, что графы изоморфны.

• (G ₁ ≡ G ₂ ) тогда и только тогда, когда ( G ₁ — ≡ G ₂ — ), где G ₁ и G ₂ — простые графы.

• (G ₁ ≡ G ₂ ), если матрицы смежности G ₁ и G ₂ совпадают.

• (G ₁ ≡ G ₂ ) тогда и только тогда, когда соответствующие подграфы G ₁ и G ₂ (полученные путем удаления некоторых вершин в G ₁ и их изображений в графе G ₂ ) изоморфны.

(G ₁ ≡ G ₂ ) тогда и только тогда, когда ( G ₁ — ≡ G ₂ — ), где G ₁ и G ₂ — простые графы.

(G ₁ ≡ G ₂ ), если матрицы смежности G ₁ и G ₂ совпадают.

(G ₁ ≡ G ₂ ) тогда и только тогда, когда соответствующие подграфы G ₁ и G ₂ (полученные путем удаления некоторых вершин в G ₁ и их изображений в графе G ₂ ) изоморфны.

пример

Какие из следующих графов изоморфны?

В графе G ₃ вершина ‘w’ имеет только степень 3, тогда как все остальные вершины графа имеют степень 2. Следовательно, G ₃ не изоморфна G ₁ или G ₂ .

Принимая дополнения G ₁ и G ₂ , у вас есть —

Здесь ( G ₁ — ≡ G ₂ — ), следовательно, (G ₁ ≡ G ₂ ).

Планарные Графики

Граф «G» называется плоским, если его можно нарисовать на плоскости или сфере так, чтобы никакие два ребра не пересекали друг друга в не вершинной точке.

пример

районы

Каждый плоский план делит плоскость на связанные области, называемые областями.

пример

Степень ограниченной области r = deg (r) = Количество ребер, охватывающих области r .

deg(1) = 3
deg(2) = 4
deg(3) = 4
deg(4) = 3
deg(5) = 8

Степень неограниченной области r = deg (r) = Количество ребер, охватывающих области r .

deg(R 1 ) = 4
deg(R 2 ) = 6

На плоских графиках действуют следующие свойства:

• 1. В плоском графе с n вершинами сумма степеней всех вершин равна

  n ∑ i = 1 градус (V _i ) = 2 | E |

• 2. Согласно теореме о сумме степеней областей , в плоском графе с ‘n’ областями сумма степеней областей равна —

  n ∑ i = 1 градус (r _i ) = 2 | E |

1. В плоском графе с n вершинами сумма степеней всех вершин равна

2. Согласно теореме о сумме степеней областей , в плоском графе с ‘n’ областями сумма степеней областей равна —

На основании приведенной выше теоремы можно сделать следующие выводы:

На плоском графике

• Если степень каждой области равна K, то сумма степеней областей равна

  K | R | = 2 | E |

• Если степень каждой области не меньше K (≥ K), то

  K | R | ≤ 2 | E |

• Если степень каждой области не превышает K (≤ K), то

  K | R | ≥ 2 | E |

Если степень каждой области равна K, то сумма степеней областей равна

K | R | = 2 | E |

Если степень каждой области не меньше K (≥ K), то

K | R | ≤ 2 | E |

Если степень каждой области не превышает K (≤ K), то

K | R | ≥ 2 | E |

Примечание. Предположим, что все регионы имеют одинаковую степень.

3. Согласно формулам Эйлера на плоских графах,

• Если граф «G» является связным плоскостью, то

  | V | + | R | = | E | + 2

• Если планарный граф с компонентами ‘K’, то

  | V | + | R | = | E | + (К + 1)

Если граф «G» является связным плоскостью, то

| V | + | R | = | E | + 2

Если планарный граф с компонентами ‘K’, то

| V | + | R | = | E | + (К + 1)

Где, | V | число вершин, | E | число ребер, и | R | это количество регионов.

4. Краевое неравенство вершин

Если «G» — связный плоский граф со степенью каждой области, по крайней мере, «K», то

| E | ≤ k / k — 2 {| v | — 2}

Вы знаете, | V | + | R | = | E | + 2

K. | R | ≤ 2 | E |

K (| E | — | V | + 2) ≤ 2 | E |

(К — 2) | Е | ≤ K (| V | — 2)

| E | ≤ k / k — 2 {| v | — 2}

5. Если ‘G’ — простой связный плоский граф, то

|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4

Существует хотя бы одна вершина V ∈ G такая, что deg (V) ≤ 5

6. Если ‘G’ — простой связный плоский граф (по крайней мере с 2 ребрами) и без треугольников, то

|E| ≤ {2|V| – 4}

7. Теорема Куратовского

Граф «G» неплоский в том и только в том случае, если у «G» есть подграф, гомеоморфный K ₅ или K _3,3 .

Гомоморфизм

Два графа G ₁ и G ₂ называются гомоморфными, если каждый из этих графов можно получить из одного и того же графа ‘G’, разделив некоторые ребра графа G на большее число вершин. Взгляните на следующий пример —

Разделите ребро «rs» на два ребра, добавив одну вершину.

Графики, показанные ниже, гомоморфны первому графу.

Если G ₁ изоморфна G ₂ , то G гомеоморфна G _2, но обратное не обязательно верно.

• Любой граф с 4 или менее вершинами является плоским.

• Любой граф с 8 или менее ребрами является плоским.

• Полный граф K _n является плоским тогда и только тогда, когда n ≤ 4.

• Полный двудольный граф K _{m, n} является плоским тогда и только тогда, когда m ≤ 2 или n ≤ 2.

• Простой непланарный граф с минимальным числом вершин является полным графом K ₅ .

• Простой непланарный граф с минимальным числом ребер равен K _{3, 3} .

Любой граф с 4 или менее вершинами является плоским.

Любой граф с 8 или менее ребрами является плоским.

Полный граф K _n является плоским тогда и только тогда, когда n ≤ 4.

Полный двудольный граф K _{m, n} является плоским тогда и только тогда, когда m ≤ 2 или n ≤ 2.

Простой непланарный граф с минимальным числом вершин является полным графом K ₅ .

Простой непланарный граф с минимальным числом ребер равен K _{3, 3} .

Многогранный граф

Простой связный плоский граф называется многогранным графом, если степень каждой вершины ≥ 3, т. Е. Deg (V) ≥ 3 ∀ V ∈ G.

• 3 | В | ≤ 2 | E |
• 3 | R | ≤ 2 | E |

Теория графов — проходимость

Граф можно обойти, если вы можете нарисовать путь между всеми вершинами, не возвращаясь к одному и тому же пути. Основываясь на этом пути, есть некоторые категории, такие как путь Эйлера и схема Эйлера, которые описаны в этой главе.

Путь Эйлера

Путь Эйлера содержит каждое ребро «G» ровно один раз, а каждую вершину «G» хотя бы один раз. Связный граф G называется проходимым, если он содержит путь Эйлера.

пример

Путь Эйлера = dcabde.

Схема Эйлера

На пути Эйлера, если начальная вершина совпадает с его конечной вершиной, то она называется схемой Эйлера.

пример

Путь Эйлера = abcdagfeca.

Схема Эйлера

Связный граф ‘G’ проходим в том и только в том случае, если число вершин с нечетной степенью в G ровно 2 или 0. Связный граф G может содержать путь Эйлера, но не схему Эйлера, если он имеет ровно две вершины с странная степень.

Примечание. Этот путь Эйлера начинается с вершины нечетной степени и заканчивается другой вершиной нечетной степени.

пример

Путь Эйлера — beabdca — это не схема Эйлера, а путь Эйлера. Очевидно, что оно имеет ровно 2 вершины нечетной степени.

Примечание. Если в связном графе G число вершин с нечетной степенью = 0, то существует схема Эйлера.

Гамильтонов график

Связный граф G называется гамильтоновым графом, если существует цикл, содержащий все вершины G.

Каждый цикл является схемой, но схема может содержать несколько циклов. Такой цикл называется гамильтоновым циклом группы G.

Гамильтонов путь

Связный граф называется гамильтоновым, если он содержит каждую вершину группы G ровно один раз. Такой путь называется гамильтоновым путем .

пример

Гамильтонов путь — Эдбак.

Примечание —

• Схема Эйлера содержит каждое ребро графа ровно один раз.
• В гамильтоновом цикле некоторые ребра графа могут быть пропущены.

пример

Посмотрите на следующий график —

Для приведенного выше графика —

• Путь Эйлера существует — ложь
• Схема Эйлера существует — ложь
• Гамильтонов цикл существует — верно
• Гамильтонов путь существует — верно

У G есть четыре вершины с нечетной степенью, следовательно это не проходимо. Пропуская внутренние ребра, граф имеет гамильтонов цикл, проходящий через все вершины.

Теория графов — Примеры

В этой главе мы рассмотрим несколько стандартных примеров, чтобы продемонстрировать концепции, которые мы уже обсуждали в предыдущих главах.

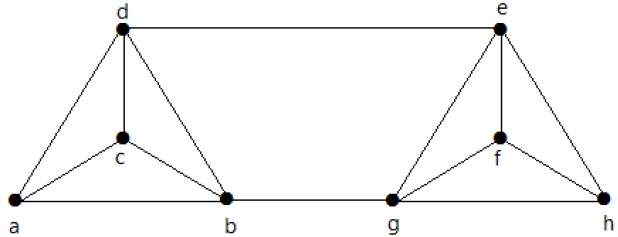
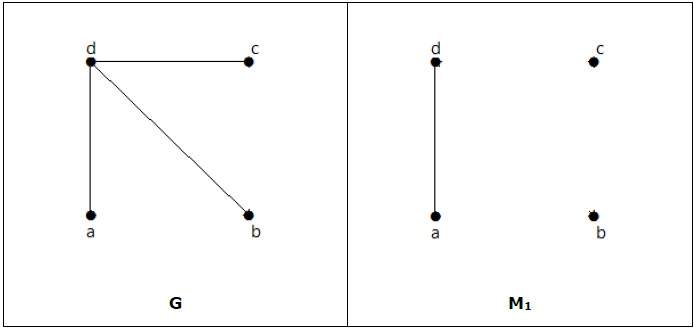
Пример 1

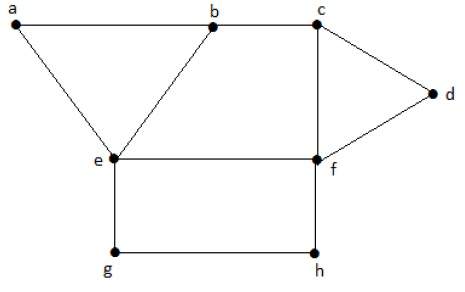
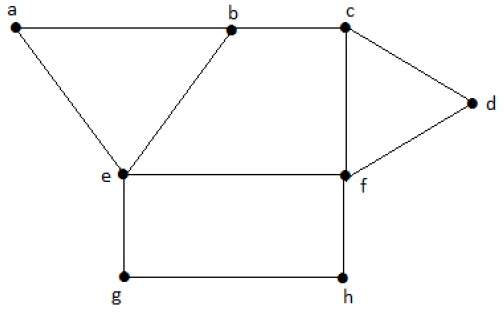
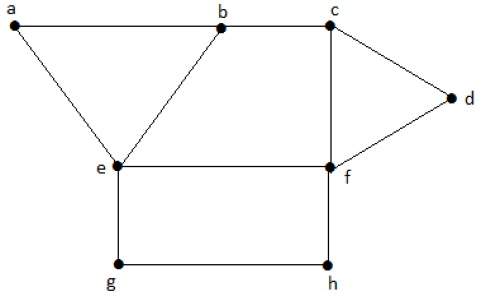
Найдите количество связующих деревьев на следующем графике.

Решение

Число связующих деревьев, полученных из приведенного выше графика, равно 3. Они следующие:

Эти три являются связующими деревьями для данных графиков. Здесь графы I и II изоморфны друг другу. Ясно, что число неизоморфных остовных деревьев равно двум.

Пример 2

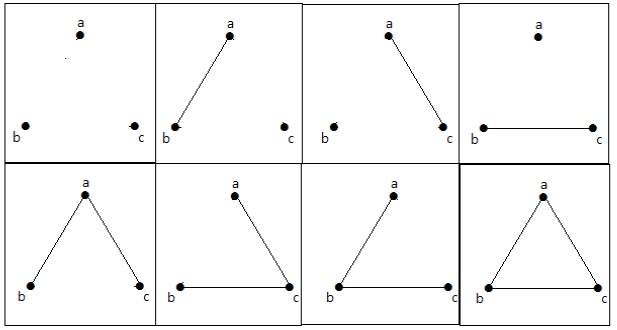
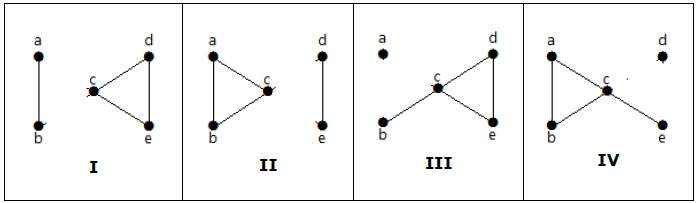
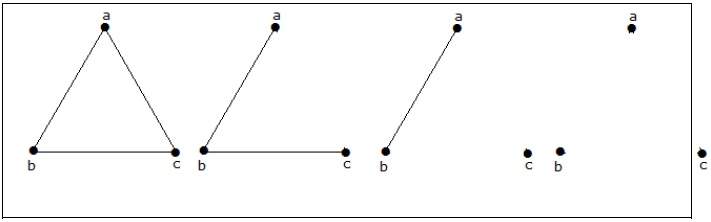
Сколько простых неизоморфных графов возможно с 3 вершинами?

Решение

Возможны 4 неизоморфных графа с 3 вершинами. Они показаны ниже.

Пример 3

Пусть ‘G’ — связный планарный граф с 20 вершинами и степень каждой вершины равна 3. Найдите количество областей в графе.

Решение

По теореме о сумме степеней

20 ∑ i = 1 градус (V _i ) = 2 | E |

20 (3) = 2 | E |

| E | = 30

По формуле Эйлера,

| V | + | R | = | E | + 2

20+ | R | = 30 + 2

| R | = 12

Следовательно, количество регионов составляет 12.

Пример 4

Какое хроматическое число полного графа K _n ?

Решение

В полном графе каждая вершина смежна с оставшимися (n – 1) вершинами. Следовательно, каждая вершина требует нового цвета. Следовательно, хроматическое число K _n = n .

Пример 5

Какой совпадает номер для следующего графика?

Решение

Количество вершин = 9

Мы можем сопоставить только 8 вершин.

Соответствующий номер 4.

Пример 6

Какое количество строк покрывает число для следующего графика?

Решение

Количество вершин = | V | = n = 7

Номер покрытия линии = (α ₁ ) ≥ ⌈ n / 2 ⌉ = 3

α ₁ ≥ 3

Используя 3 ребра, мы можем покрыть все вершины.

Следовательно, номер покрытия строки равен 3.