Покрывающий граф — это подграф, который содержит либо все вершины, либо все ребра, соответствующие некоторому другому графу. Подграф, который содержит все вершины, называется покрытием линии / ребра . Подграф, содержащий все ребра, называется покрытием вершин .
Линия покрытия
Пусть G = (V, E) — граф. Подмножество C (E) называется покрытием линий G, если каждая вершина G инцидентна хотя бы с одним ребром в C, т. Е.
deg (V) ≥ 1 ∀ V ∈ G
потому что каждая вершина связана с другой вершиной ребром. Следовательно, он имеет минимальную степень 1.
пример
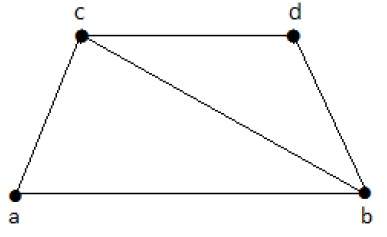
Посмотрите на следующий график —
Его подграфы, имеющие покрытие строк:
C 1 = {{a, b}, {c, d}}
C 2 = {{a, d}, {b, c}}
C 3 = {{a, b}, {b, c}, {b, d}}
C 4 = {{a, b}, {b, c}, {c, d}}
Покрытие линии ‘G’ не существует тогда и только тогда, когда ‘G’ имеет изолированную вершину. Линейное покрытие графа с «n» вершинами имеет не менее ⌊ n 2 ⌋ ребер.
Минимальная линия покрытия
Линия, покрывающая C графа G, называется минимальной, если никакое ребро не может быть удалено из C.
пример
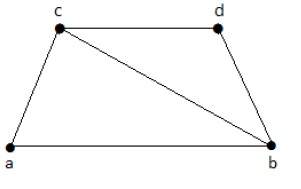
На приведенном выше графике подграфы, имеющие покрытие строк, выглядят следующим образом:
C 1 = {{a, b}, {c, d}}
C 2 = {{a, d}, {b, c}}
C 3 = {{a, b}, {b, c}, {b, d}}
C 4 = {{a, b}, {b, c}, {c, d}}
Здесь C 1 , C 2 , C 3 — минимальные покрытия строк, а C 4 — не потому, что мы можем удалить {b, c}.
Минимальное покрытие линии
Это также известно как Наименьшее Минимальное Покрытие Линии . Минимальное покрытие линий с минимальным числом ребер называется минимальным покрытием линий в G. Число ребер в минимальном покрытии линии в «G» называется числом покрытия линии в «G» (α 1 ).
пример
В приведенном выше примере C 1 и C 2 являются минимальным покрытием линий G и α 1 = 2.
-
Каждое линейное покрытие содержит минимальное линейное покрытие.
-
Каждое покрытие строк не содержит минимального покрытия строк (C 3 не содержит минимального покрытия линий.
-
Ни одно минимальное покрытие строк не содержит циклов.
-
Если линия, покрывающая «C», не содержит путей длиной 3 или более, то «C» — это минимальное покрытие линий, поскольку все компоненты «C» являются звездным графом и из звездного графа ни одно ребро не может быть удалено.
Каждое линейное покрытие содержит минимальное линейное покрытие.
Каждое покрытие строк не содержит минимального покрытия строк (C 3 не содержит минимального покрытия линий.
Ни одно минимальное покрытие строк не содержит циклов.
Если линия, покрывающая «C», не содержит путей длиной 3 или более, то «C» — это минимальное покрытие линий, поскольку все компоненты «C» являются звездным графом и из звездного графа ни одно ребро не может быть удалено.
Покрытие вершин
Пусть ‘G’ = (V, E) — граф. Подмножество K из V называется покрытием вершин из ‘G’, если каждое ребро из ‘G’ инцидентно или покрыто вершиной в ‘K’.
пример
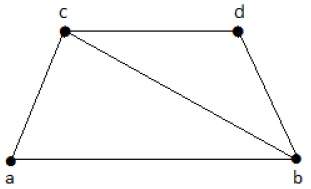
Посмотрите на следующий график —
Подграфы, которые могут быть получены из приведенного выше графика, следующие:
K 1 = {b, c}
K 2 = {a, b, c}
K 3 = {b, c, d}
K 4 = {a, d}
Здесь K 1 , K 2 и K 3 имеют покрытие вершин, тогда как K 4 не имеет покрытия вершин, поскольку оно не покрывает ребро {bc}.
Минимальное покрытие вершин
Вершина «K» графа «G» называется минимальным покрытием вершин, если ни одна вершина не может быть удалена из «K».
пример
На приведенном выше графике подграфы, имеющие покрытие вершин, выглядят следующим образом:
K 1 = {b, c}
K 2 = {a, b, c}
K 3 = {b, c, d}
Здесь K 1 и K 2 являются минимальными покрытиями вершин, тогда как в K 3 вершина ‘d’ может быть удалена.
Минимальное покрытие вершин
Он также известен как наименьшее минимальное покрытие вершин. Минимальное покрытие вершин графа G с минимальным количеством вершин называется минимальным покрытием вершин.
Число вершин в минимальном покрытии вершин из G называется числом вершин, покрывающим G (α 2 ).
пример
На следующем графике подграфы, имеющие покрытие вершин, выглядят следующим образом:
K 1 = {b, c}
K 2 = {a, b, c}
K 3 = {b, c, d}
Здесь K 1 — минимальное покрытие вершин G, поскольку оно имеет только две вершины. α 2 = 2.