Соответствующий граф — это подграф графа, в котором нет смежных ребер. Просто между двумя ребрами не должно быть общей вершины.
согласование
Пусть ‘G’ = (V, E) — граф. Подграф называется совпадающим M (G), если каждая вершина из G инцидентна не более чем с одним ребром в M, т. Е.
deg (V) ≤ 1 ∀ V ∈ G
это означает, что в совпадающем графе M (G) вершины должны иметь степень 1 или 0, где ребра должны падать от графа G.
Обозначение — M (G)
пример
В соответствии
если deg (V) = 1, то (V) называется соответствующим
если deg (V) = 0, то (V) не совпадает.
В сопоставлении нет двух соседних ребер. Это потому, что если любые два ребра смежны, то степень вершины, соединяющей эти два ребра, будет иметь степень 2, которая нарушает правило сопоставления.
Максимальное соответствие
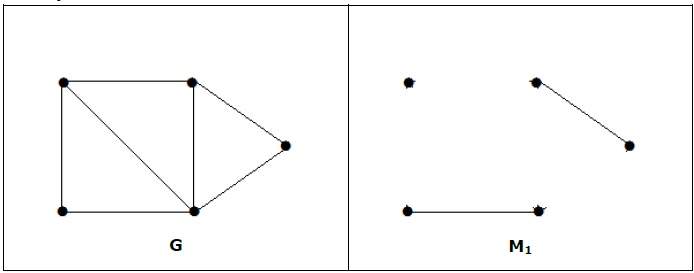
Соответствующий M графа ‘G’ называется максимальным, если никакие другие ребра G не могут быть добавлены к M.
пример
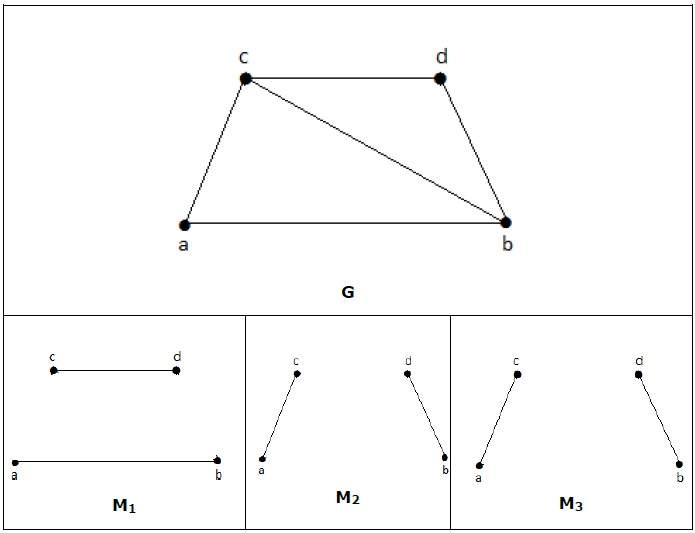
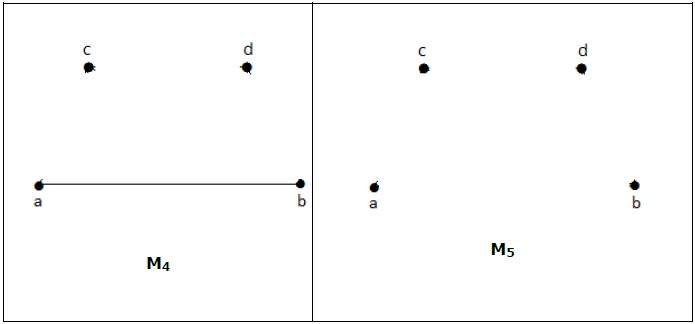
M 1 , M 2 , M 3 из приведенного выше графика — максимальное совпадение G.
Максимальное соответствие
Это также известно как наибольшее максимальное соответствие. Максимальное соответствие определяется как максимальное соответствие с максимальным количеством ребер.
Число ребер в максимальном совпадении «G» называется его совпадающим номером .
пример
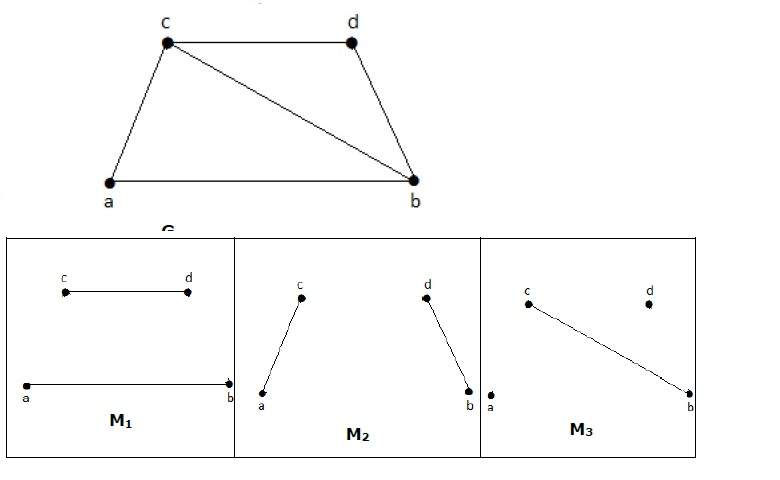
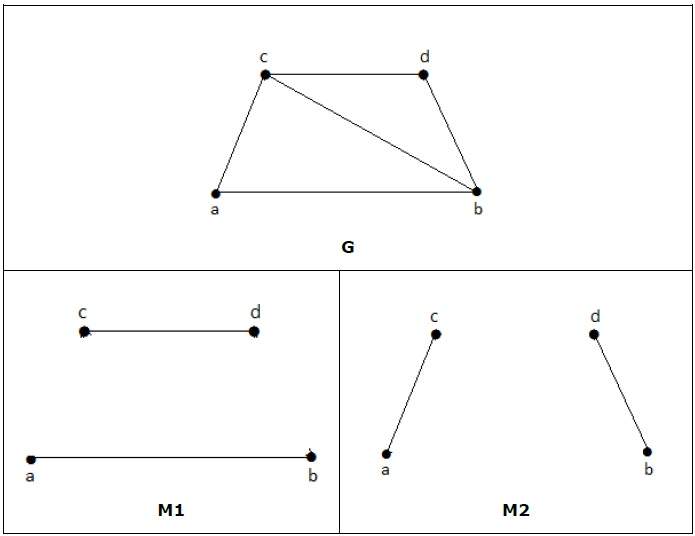
Для графа, приведенного в приведенном выше примере, M 1 и M 2 являются максимальным соответствием ‘G’, а его номер совпадения равен 2. Следовательно, используя граф G, мы можем сформировать только подграфы с максимум 2 ребрами. Следовательно, у нас есть совпадающее число как два.
Идеальное соответствие
Сопоставление (M) графа (G) называется совершенным совпадением, если каждая вершина графа g (G) инцидентна ровно одному ребру совпадающего (M), т.е.
град (V) = 1 ∀ V
Степень каждой вершины в подграфе должна иметь степень 1.
пример
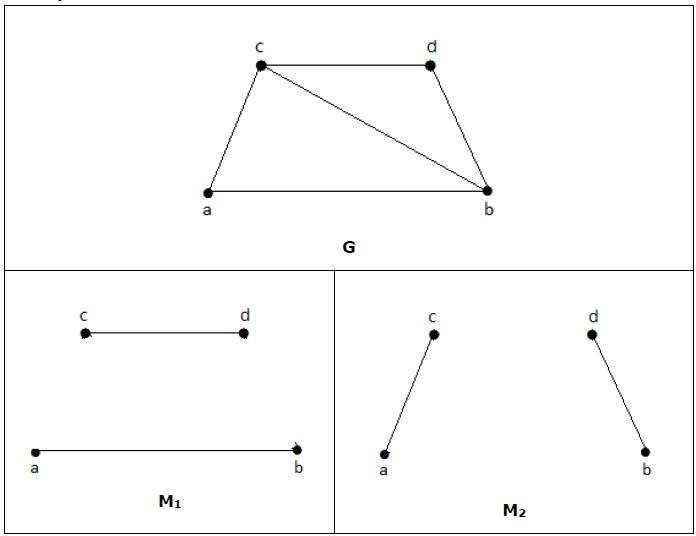
На следующих графиках M 1 и M 2 являются примерами идеального соответствия G.
Примечание. Каждое идеальное соответствие графа также является максимальным соответствием графа, поскольку нет шансов добавить еще одно ребро в графе идеального соответствия.
Максимальное соответствие графа не обязательно должно быть идеальным. Если граф «G» имеет идеальное совпадение, то число вершин | V (G) | даже. Если это нечетно, то последняя вершина соединяется с другой вершиной, и, наконец, остается одна вершина, которая не может быть спарена с любой другой вершиной, для которой степень равна нулю. Это явно нарушает принцип идеального соответствия.
пример
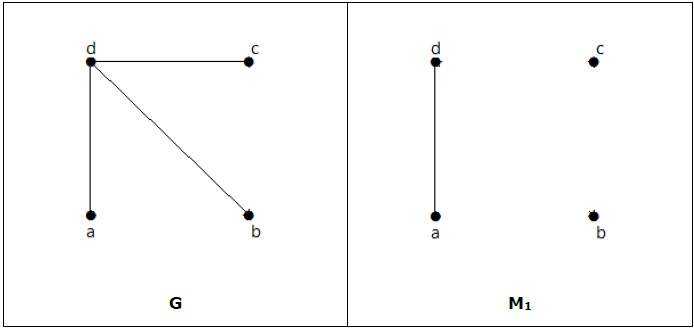
Примечание . Обратное утверждение выше не обязательно должно быть верным. Если G имеет четное число вершин, то M 1 не обязательно должно быть совершенным.
пример
Это совпадение, но оно не является идеальным, даже если оно имеет четное количество вершин.