Возможен ли переход графа из одной вершины в другую, определяется тем, как граф связан. Связность является основной концепцией в теории графов. Связность определяет, подключен ли график или нет. Он имеет подтемы, основанные на ребре и вершине, известные как связность ребер и вершин. Давайте обсудим их подробно.
связь
Граф называется связным, если между каждой парой вершин есть путь . От каждой вершины к любой другой вершине должен быть некоторый путь для прохождения. Это называется связностью графа. Граф с несколькими несвязанными вершинами и ребрами называется несвязным.
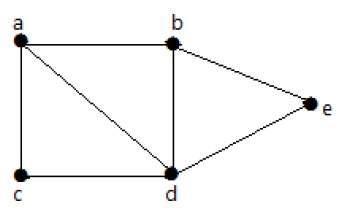
Пример 1
На следующем графике можно перейти от одной вершины к любой другой вершине. Например, можно перейти от вершины «а» к вершине «е», используя путь «ab-e».
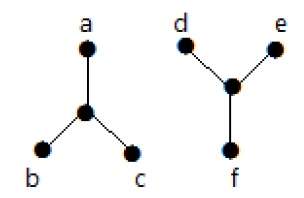
Пример 2
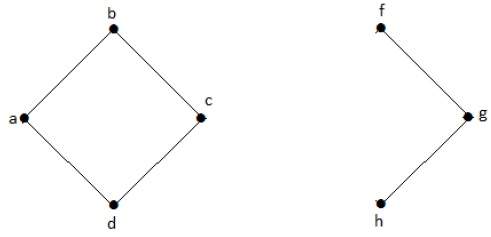
В следующем примере переход от вершины ‘a’ к вершине ‘f’ невозможен, поскольку между ними нет прямого или косвенного пути. Следовательно, это несвязный граф.
Cut Vertex
Пусть ‘G’ связный граф. Вершина V ∈ G называется разрезанной вершиной из «G», если «G-V» (исключить «V» из «G») приводит к несвязному графу. Удаление вырезанной вершины из графа разбивает ее на два или более графа.
Примечание. Удаление обрезанной вершины может привести к отключению графа.
Связный граф ‘G’ может иметь не более (n – 2) вершин среза.
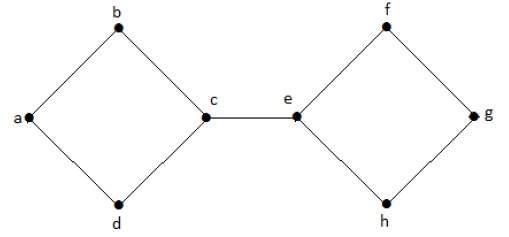
пример
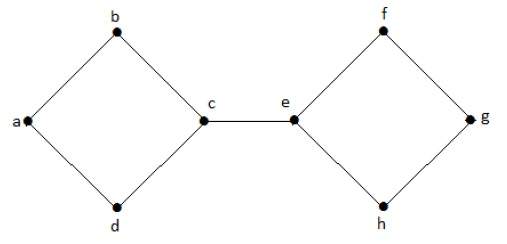
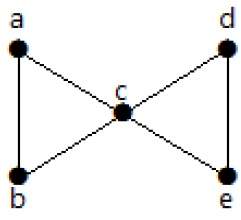
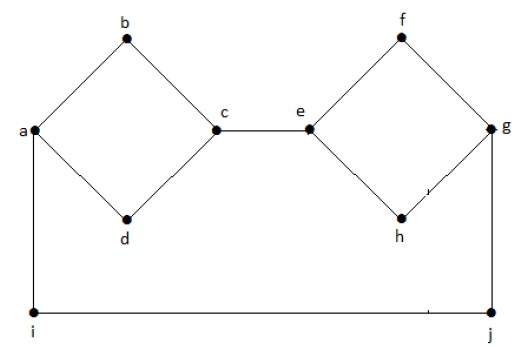
На следующем графике вершины ‘e’ и ‘c’ являются вырезанными вершинами.
Удалив «е» или «с», граф станет несвязным графом.
Без ‘g’ нет пути между вершиной ‘c’ и вершиной ‘h’ и многими другими. Следовательно, это несвязный граф с разрезанной вершиной в виде «е». Точно так же ‘c’ также является вершиной разреза для приведенного выше графа.
Cut Edge (Мост)
Пусть ‘G’ связный граф. Ребро «e» ∈ G называется отрезанным ребром, если «G-e» приводит к несвязному графу.
Если удаление ребра в графе приводит к двум или более графам, то это ребро называется Cut Edge.
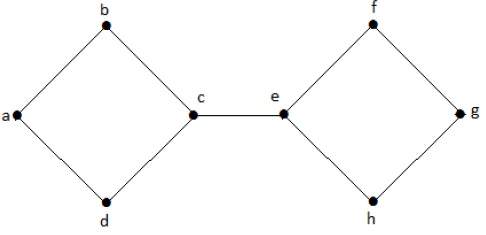
пример
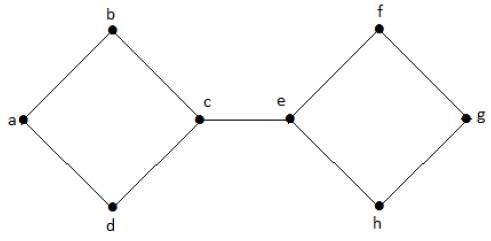
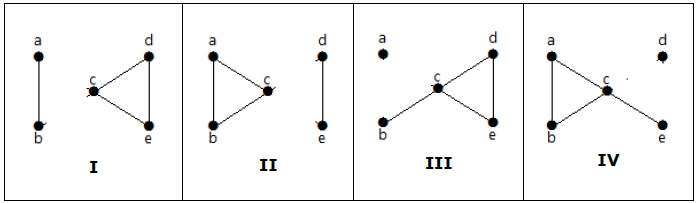
На следующем графике край обрезки равен [(c, e)]
Удаляя ребро (c, e) из графа, он становится несвязным графом.
В приведенном выше графике удаление ребра (c, e) разбивает граф на два, что является ничем иным, как несвязным графом. Следовательно, ребро (c, e) является отрезанным ребром графа.
Примечание. Пусть «G» — связный граф с «n» вершинами, тогда
-
отрезок e ∈ G тогда и только тогда, когда ребро «e» не является частью какого-либо цикла в G.
-
Максимально возможное количество режущих кромок равно n-1.
-
всякий раз, когда существуют ребра среза, вершины среза также существуют, потому что по крайней мере одна вершина среза является вершиной среза.
-
если вершина разреза существует, то край разреза может существовать или не существовать.
отрезок e ∈ G тогда и только тогда, когда ребро «e» не является частью какого-либо цикла в G.
Максимально возможное количество режущих кромок равно n-1.
всякий раз, когда существуют ребра среза, вершины среза также существуют, потому что по крайней мере одна вершина среза является вершиной среза.
если вершина разреза существует, то край разреза может существовать или не существовать.
Вырезать набор графика
Пусть ‘G’ = (V, E) связный граф. Подмножество E ‘E называется нарезанным множеством G, если удаление всех ребер E’ из G приводит к разъединению G.
Если удаление определенного числа ребер из графа делает его отключенным, то эти удаленные ребра называются набором вырезов графа.
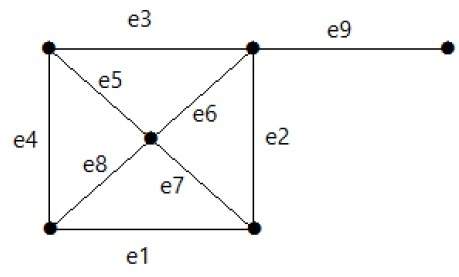
пример
Посмотрите на следующий график. Его набор срезов E1 = {e1, e3, e5, e8}.
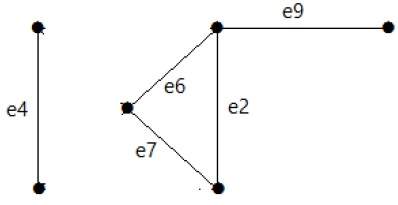
После удаления набора вырезок E1 из графика это будет выглядеть следующим образом:
Точно так же есть другие наборы разрезов, которые могут отключить график —
- E3 = {e9} — наименьший набор вырезов графа.
- E4 = {e3, e4, e5}
Edge Connectivity
Пусть ‘G’ связный граф. Минимальное количество ребер, удаление которых приводит к отключению G, называется связностью ребер G.
Обозначение — λ (G)
Другими словами, число ребер в наименьшем отрезке G называется связностью ребер G.
Если «G» имеет ребро среза, то λ (G) равно 1. (связность ребра G.)
пример
Посмотрите на следующий график. Удаляя два минимальных ребра, связный граф становится несвязным. Следовательно, его краевая связность (λ (G)) равна 2.
Вот четыре способа отключить график, удалив два ребра:
Vertex Connectivity
Пусть ‘G’ связный граф. Минимальное количество вершин, удаление которых делает «G» либо несвязным, либо сокращает «G» до тривиального графа, называется связностью его вершин.
Обозначение — K (G)
пример
В приведенном выше графике удаление вершин ‘e’ и ‘i’ делает граф отключенным.
Если G имеет вырезанную вершину, то K (G) = 1.
Обозначение — Для любого связного графа G,
K (G) ≤ λ (G) ≤ δ (G)
Связность вершин (K (G)), связность ребер (λ (G)), минимальное количество градусов G (δ (G)).
пример
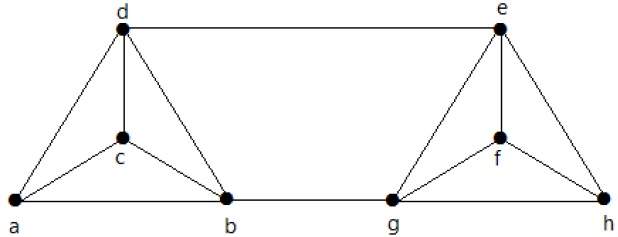
Вычислить λ (G) и K (G) для следующего графика —
Решение
Из графика
δ (G) = 3
K (G) ≤ λ (G) ≤ δ (G) = 3 (1)
K (G) ≥ 2 (2)
Удалив ребра {d, e} и {b, h}, мы можем отключить G.
Следовательно,
λ (G) = 2
2 ≤ λ (G) ≤ δ (G) = 2 (3)
Из (2) и (3) связность вершин K (G) = 2