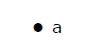Существуют различные типы графиков в зависимости от количества вершин, количества ребер, взаимосвязанности и их общей структуры. Мы обсудим только несколько важных типов графиков в этой главе.
Нулевой график
Граф, не имеющий ребер , называется нулевым графом .
пример
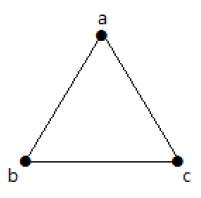
На приведенном выше графике есть три вершины с именами «a», «b» и «c», но среди них нет ребер. Следовательно, это нулевой граф.
Тривиальный график
Граф с единственной вершиной называется тривиальным графом .
пример
На приведенном выше графике есть только одна вершина «а» без других ребер. Следовательно, это тривиальный граф.
Ненаправленный граф
Ненаправленный граф содержит ребра, но ребра не являются ориентированными.
пример
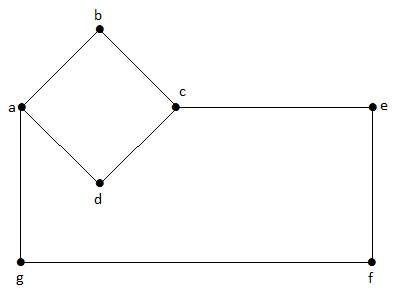
В этом графе «a», «b», «c», «d», «e», «f», «g» — вершины, а «ab», «bc», «cd», «da». ‘,’ ag ‘,’ gf ‘,’ ef ‘- ребра графа. Поскольку это ненаправленный граф, ребра «ab» и «ba» совпадают. Точно так же другие ребра также рассматриваются аналогичным образом.
Направленный граф
В ориентированном графе каждое ребро имеет направление.
пример
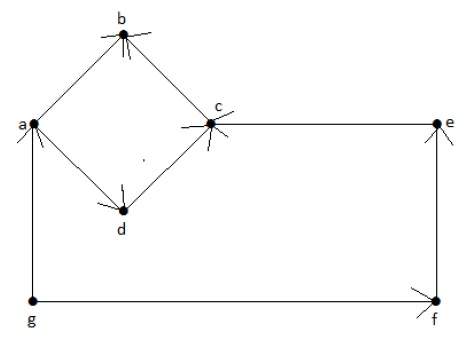
На приведенном выше графике у нас есть семь вершин «a», «b», «c», «d», «e», «f» и «g», и восемь ребер «ab», «cb», « dc ‘,’ ad ‘,’ ec ‘,’ fe ‘,’ gf ‘и’ ga ‘. Поскольку это ориентированный граф, на каждом ребре есть метка стрелки, показывающая его направление. Обратите внимание, что в ориентированном графе «ab» отличается от «ba».
Простой график
Граф без петель и параллельных ребер называется простым графом.
-
Максимально возможное число ребер в одном графе с n вершинами равно n C 2, где n C 2 = n (n — 1) / 2.
-
Число простых графов возможно с n вершинами = 2 n c 2 = 2 n (n-1) / 2 .
Максимально возможное число ребер в одном графе с n вершинами равно n C 2, где n C 2 = n (n — 1) / 2.
Число простых графов возможно с n вершинами = 2 n c 2 = 2 n (n-1) / 2 .
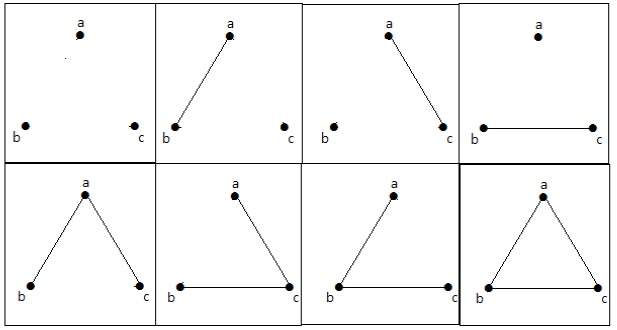
пример
На следующем графике есть 3 вершины с 3 ребрами, которые являются максимальными, исключая параллельные ребра и петли. Это можно доказать с помощью приведенных выше формул.
Максимальное количество ребер с n = 3 вершинами —
n C 2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges
Максимальное количество простых графов с n = 3 вершинами —
2 n C 2 = 2 n(n-1)/2 = 2 3(3-1)/2 = 2 3 = 8
Эти 8 графиков, как показано ниже —
Связанный график
Граф G называется связным, если между каждой парой вершин существует путь . Для каждой вершины графа должно быть хотя бы одно ребро. Так что мы можем сказать, что он связан с какой-то другой вершиной на другой стороне ребра.
пример
На следующем графике каждая вершина имеет свое ребро, соединенное с другим ребром. Следовательно, это связный граф.
Отключенный график
Граф G несвязен, если он не содержит хотя бы двух связанных вершин.
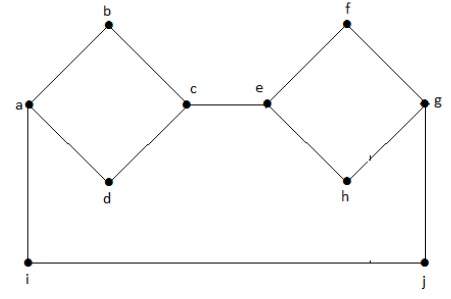
Пример 1
Следующий график является примером отключенного графа, где есть два компонента, один с вершинами «a», «b», «c», «d», а другой с «e», «f», «g», ‘h’ вершины.
Два компонента независимы и не связаны друг с другом. Следовательно, он называется несвязным графом.
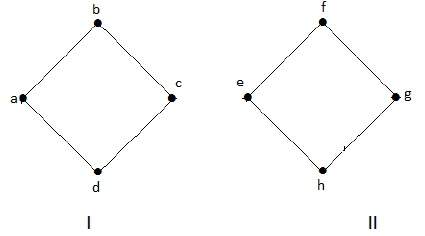
Пример 2
В этом примере есть два независимых компонента, abfe и cd, которые не связаны друг с другом. Следовательно, это несвязный граф.
Обычный график
Граф G называется регулярным, если все его вершины имеют одинаковую степень . В графе, если степень каждой вершины равна «k», то этот граф называется «k-регулярным графом».
пример
На следующих графиках все вершины имеют одинаковую степень. Поэтому эти графы называются регулярными графами.
В обоих графах все вершины имеют степень 2. Они называются 2-регулярными графами.
Полный график
Простой граф с «n» взаимными вершинами называется полным графом и обозначается «K n » . В графе вершина должна иметь ребра со всеми остальными вершинами, тогда она называется полным графом.
Другими словами, если вершина связана со всеми остальными вершинами графа, то она называется полным графом.
пример
В следующих графах каждая вершина графа связана со всеми остальными вершинами графа, кроме самой себя.
На графике я
| б | с | ||
|---|---|---|---|
| Нет соединения | Связано | Связано | |
| б | Связано | Нет соединения | Связано |
| с | Связано | Связано | Нет соединения |
На графике II
| п | Q | р | s | |
|---|---|---|---|---|
| п | Нет соединения | Связано | Связано | Связано |
| Q | Связано | Нет соединения | Связано | Связано |
| р | Связано | Связано | Нет соединения | Связано |
| s | Связано | Связано | Связано | Нет соединения |
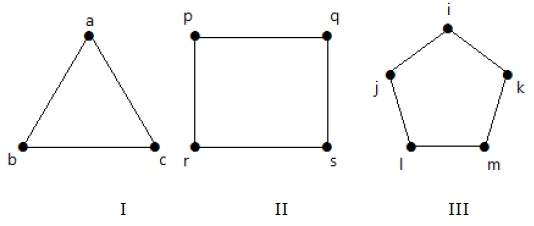
Цикл графика
Простой граф с n вершинами (n> = 3) и ребрами n называется графом циклов, если все его ребра образуют цикл длины n.
Если степень каждой вершины в графе равна двум, то она называется циклическим графом .
Обозначение — C n
пример
Посмотрите на следующие графики —
-
Граф I имеет 3 вершины с 3 ребрами, которые образуют цикл ‘ab-bc-ca’.
-
Граф II имеет 4 вершины с 4 ребрами, которые образуют цикл ‘pq-qs-sr-rp’.
-
Граф III имеет 5 вершин с 5 ребрами, которые образуют цикл ‘ik-km-ml-lj-ji’.
Граф I имеет 3 вершины с 3 ребрами, которые образуют цикл ‘ab-bc-ca’.
Граф II имеет 4 вершины с 4 ребрами, которые образуют цикл ‘pq-qs-sr-rp’.
Граф III имеет 5 вершин с 5 ребрами, которые образуют цикл ‘ik-km-ml-lj-ji’.
Следовательно, все данные графы являются графами циклов.
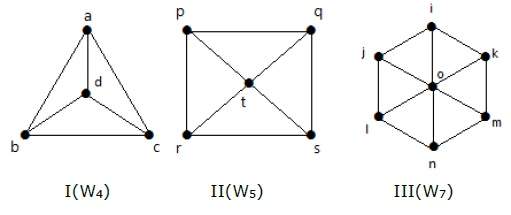
Колесо График
Граф колеса получается из графа циклов C n-1 путем добавления новой вершины. Эта новая вершина называется Hub, которая связана со всеми вершинами C n .
Обозначение — W n
No. of edges in W n = No. of edges from hub to all other vertices +
No. of edges from all other nodes in cycle graph without a hub.
= (n–1) + (n–1)
= 2(n–1)
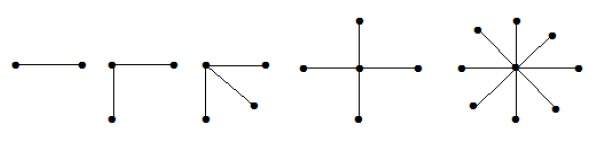
пример
Посмотрите на следующие графики. Они все колесные графики.
На графике I он получен из C 3 путем добавления вершины в середине, названной ‘d’. Обозначается как W 4 .
Number of edges in W 4 = 2(n-1) = 2(3) = 6
На графике II он получен из C 4 путем добавления вершины в середине, названной ‘t’. Обозначается как W 5 .
Number of edges in W 5 = 2(n-1) = 2(4) = 8
На графике III он получен из C 6 путем добавления вершины в середине, названной ‘o’. Обозначается как W 7 .
Number of edges in W 4 = 2(n-1) = 2(6) = 12
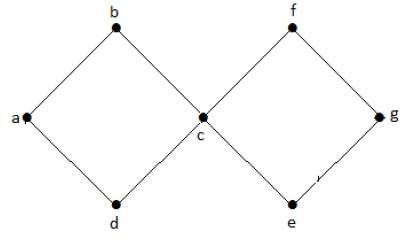
Циклический график
Граф с хотя бы одним циклом называется циклическим графом.
пример
В приведенном выше примере графа у нас есть два цикла abcda и cfgec. Следовательно, он называется циклическим графом.
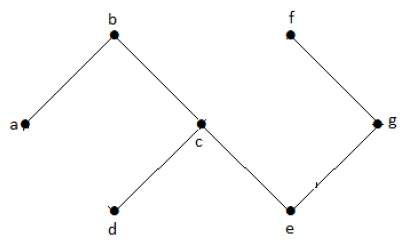
Ациклический Граф
Граф без циклов называется ациклическим графом.
пример
В приведенном выше примере графа у нас нет циклов. Следовательно, это нециклический граф.
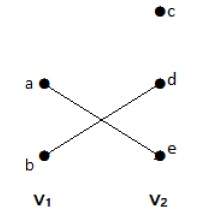
Двудольный график
Простой граф G = (V, E) с разбиением вершин V = {V 1 , V 2 } называется двудольным графом, если каждое ребро E соединяет вершину в V 1 с вершиной в V 2 .
В общем случае бипертитовый граф имеет два набора вершин, скажем, V 1 и V 2 , и если ребро нарисовано, он должен соединить любую вершину в наборе V 1 с любой вершиной в наборе V 2 .
пример
На этом графике вы можете наблюдать два набора вершин — V 1 и V 2 . Здесь два ребра с именами «ae» и «bd» соединяют вершины двух множеств V 1 и V 2.
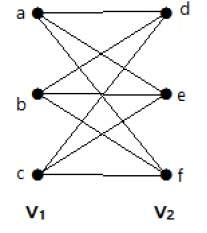
Полный двудольный график
Двудольный граф ‘G’, G = (V, E) с разбиением V = {V 1 , V 2 } называется полным двудольным графом, если каждая вершина в V 1 соединена с каждой вершиной V 2 .
В общем, полный двудольный граф соединяет каждую вершину из множества V 1 с каждой вершиной из множества V 2 .
пример
Следующий граф является полным двудольным графом, потому что у него есть ребра, соединяющие каждую вершину из множества V 1 с каждой вершиной из множества V 2 .
Если | V 1 | = m и | V 2 | = n, то полный двудольный граф обозначается через K m, n .
-
K m, n имеет (m + n) вершин и (mn) ребер.
-
K m, n регулярный граф, если m = n.
K m, n имеет (m + n) вершин и (mn) ребер.
K m, n регулярный граф, если m = n.
В общем случае полный двудольный граф не является полным графом .
K m, n полный граф, если m = n = 1.
Максимальное число ребер в двудольном графе с n вершинами
]
Если n = 10, k5, 5 = ⌊ n 2/4 ⌋ = ⌊ 10 2/4 ⌋ = 25
Аналогично К6, 4 = 24
К7, 3 = 21
К8, 2 = 16
К9, 1 = 9
Если n = 9, k5, 4 = ⌊ n 2/4 ⌋ = ⌊ 9 2/4 ⌋ = 20
Аналогично К6, 3 = 18
К7, 2 = 14
К8, 1 = 8
«G» является двудольным графом, если в «G» нет циклов нечетной длины. Частным случаем двудольного графа является звездный граф .
Звездный График
Полный двудольный граф вида K 1, n-1 является графом звезд с n-вершинами. Звездный граф является полным двудольным графом, если одна вершина принадлежит одному набору, а все остальные вершины принадлежат другому набору.
пример
На приведенных выше графиках из n вершин все n – 1 вершины связаны с одной вершиной. Следовательно, оно имеет вид K 1, n-1, которые являются графами звезд.
Дополнение графика
Пусть ‘ G — ‘ — простой граф с некоторыми вершинами, такими как у G, и ребро {U, V} присутствует в ‘ G — ‘ , если ребро отсутствует в G. Это означает, что две вершины смежны в « G — », если две вершины не смежны в G.
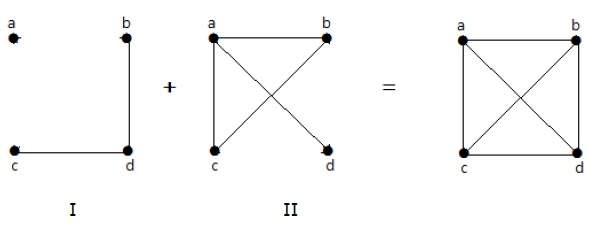
Если ребра, которые существуют в графе I, отсутствуют в другом графе II, и если граф I и граф II объединены вместе, чтобы сформировать полный граф, то граф I и граф II называются дополнениями друг друга.
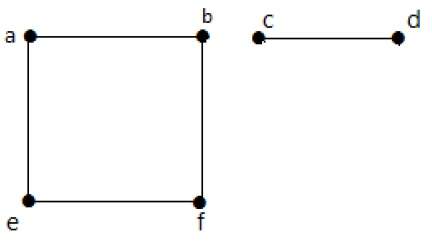
пример
В следующем примере graph-I имеет два ребра: «cd» и «bd». Его граф дополнения II имеет четыре ребра.
Обратите внимание, что ребра в графе-I отсутствуют в графе-II и наоборот. Следовательно, комбинация обоих графов дает полный граф из n вершин.
Примечание . Сочетание двух дополнительных графов дает полный граф.
Если «G» — простой граф, то
| E (G) | + | E ( ‘ G — ‘ ) | = | E (K n ) |, где n = количество вершин в графе.
пример
Пусть ‘G’ — простой граф с девятью вершинами и двенадцатью ребрами, найдите число ребер в ‘ G — ‘ .
У вас есть, | E (G) | + | E ( ‘ G — ‘ ) | = | E (K n ) |
12 + | E ( ‘ G — ‘ ) | знак равно
9 (9-1) 2 = 9 C 2
12 + | E ( ‘ G — ‘ ) | = 36
| E ( ‘ G — ‘ ) | = 24
«G» — простой граф с 40 ребрами, а его дополнение « G — » имеет 38 ребер. Найдите количество вершин в графе G или ‘ G — ‘ .
Пусть количество вершин в графе равно n.
Имеем, | E (G) | + | E ( ‘ G — ‘ ) | = | E (K n ) |
40 + 38 = n (n-1) 2
156 = n (n-1)
13 (12) = n (n-1)
n = 13