Раскраска графа — это не более чем простой способ маркировки компонентов графа, таких как вершины, ребра и области, при некоторых ограничениях. На графике нет двух смежных вершин, смежных ребер или смежных областей, окрашенных минимальным количеством цветов. Это число называется хроматическим числом, а граф называется правильно окрашенным графом .
Во время раскраски графа на графике устанавливаются следующие ограничения: цвета, порядок окраски, способ назначения цвета и т. Д. Раскраска присваивается вершине или конкретной области. Таким образом, вершины или области, имеющие одинаковые цвета, образуют независимые множества.
Окраска вершин
Раскраска вершин — это присвоение цветов вершинам графа G так, что никакие две смежные вершины не имеют одинакового цвета. Проще говоря, две вершины ребра не должны быть одного цвета.
Хроматическое число
Минимальное количество цветов, необходимое для раскраски вершин графа G, называется хроматическим числом G, обозначаемым X (G).
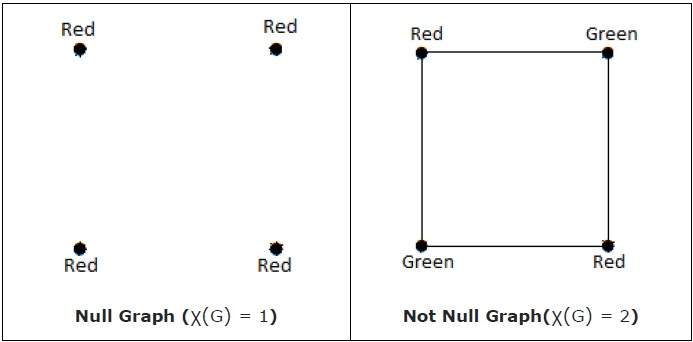
χ (G) = 1 тогда и только тогда, когда «G» является нулевым графом. Если ‘G’ не нулевой граф, то χ (G) ≥ 2
пример
Примечание . Граф ‘G’ называется n-покрываемым, если существует раскраска вершин, использующая не более n цветов, т. Е. X (G) ≤ n.
Окраска региона
Раскраска областей — это присвоение цветов областям плоского графа, чтобы ни у двух соседних областей не было одинакового цвета. Говорят, что две области являются смежными, если они имеют общее ребро.
пример
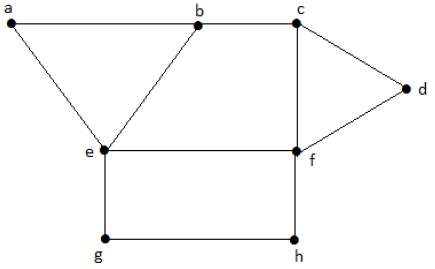
Посмотрите на следующий график. Регионы ‘aeb’ и ‘befc’ являются смежными, поскольку между этими двумя регионами существует общая граница ‘be’.
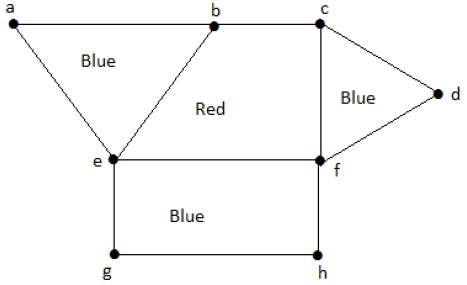
Точно так же другие области также окрашены в зависимости от смежности. Этот график раскрашен следующим образом —
пример
Хроматическое число K n равно
а) н
б) n – 1
в) ⌊ н 2 ⌋
г) ⌈ н 2 ⌉
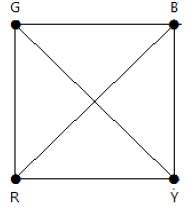
Рассмотрим этот пример с K 4 .
В полном графе каждая вершина смежна с остальными (n — 1) вершинами. Следовательно, каждая вершина требует нового цвета. Следовательно, хроматическое число K n = n.
Приложения для раскраски графиков
Раскраска графа является одним из важнейших понятий в теории графов. Он используется во многих приложениях информатики в реальном времени, таких как —