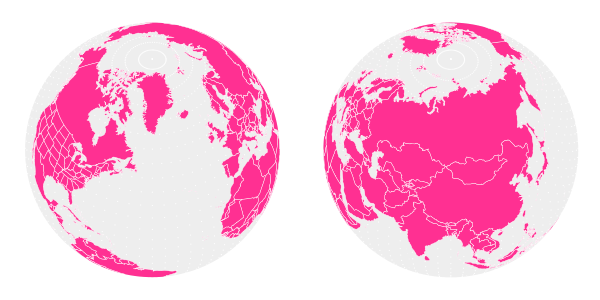
В этом уроке я покажу вам, как взять карту SVG и спроецировать ее на глобус в виде вектора. Чтобы выполнить математические преобразования, необходимые для проецирования карты на сферу, мы должны использовать сценарии Python для чтения данных карты и преобразования их в изображение земного шара. В этом руководстве предполагается, что вы используете Python 3.4, последний доступный Python.
В Inkscape есть своего рода Python API, который можно использовать для самых разных вещей. Однако, поскольку нас интересует только преобразование форм, проще написать отдельную программу, которая самостоятельно читает и печатает файлы SVG.
1. Отформатируйте карту
Тип карты, который мы хотим, называется равносторонней картой. На равносторонней карте долгота и широта места соответствуют его координатам x и y на карте. Одна равносторонняя карта мира может быть найдена на Wikimedia Commons (здесь есть версия с американскими штатами ).
Координаты SVG могут быть определены различными способами. Например, они могут быть относительно ранее определенной точки или определены абсолютно с начала координат. Чтобы сделать нашу жизнь проще, мы хотим преобразовать координаты на карте в абсолютную форму. Inkscape может сделать это. Перейдите в настройки Inkscape (в меню « Правка» ) и в разделе « Ввод / вывод» > « Вывод SVG» установите для формата строки пути значение « Абсолют» .
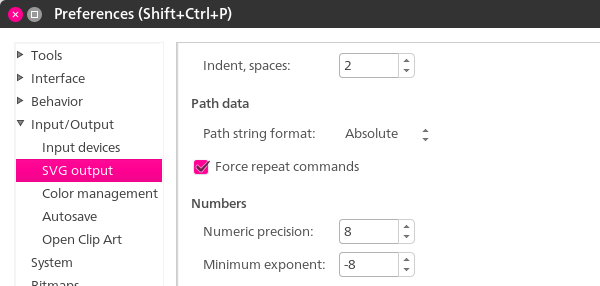
Inkscape не будет автоматически преобразовывать координаты; Вы должны выполнить какое-то преобразование путей, чтобы это произошло. Самый простой способ сделать это — просто выделить все и переместить его вверх и вниз одним нажатием каждой из стрелок вверх и вниз. Затем повторно сохраните файл.
2. Запустите свой скрипт на Python
Создайте новый файл Python. Импортируйте следующие модули:
|
1
2
3
4
5
6
7
8
|
import sys
import re
import math
import time
import datetime
import numpy as np
import xml.etree.ElementTree as ET
|
Вам нужно будет установить библиотеку NumPy , которая позволит вам выполнять определенные векторные операции, такие как скалярное произведение и перекрестное произведение
3. Математика перспективной проекции
Проецирование точки в трехмерном пространстве в двумерное изображение включает в себя поиск вектора из камеры в точку, а затем разделение этого вектора на три перпендикулярных вектора.
Два парциальных вектора, перпендикулярных вектору камеры (направление, в котором находится камера), становятся координатами x и y ортогонально проецируемого изображения. Частичный вектор, параллельный вектору камеры, становится тем, что называется расстоянием z от точки. Чтобы преобразовать ортогональное изображение в перспективное изображение, разделите каждую координату x и y на расстояние z .
На этом этапе имеет смысл определить определенные параметры камеры. Во-первых, нам нужно знать, где находится камера в трехмерном пространстве. Сохраните его координаты x , y и z в словаре.
|
1
|
camera = {‘x’: -15, ‘y’: 15, ‘z’: 30}
|
Глобус будет расположен в начале координат, поэтому имеет смысл ориентировать камеру на него. Это означает, что вектор направления камеры будет противоположен положению камеры.
|
1
|
cameraForward = {‘x’: -1*camera[‘x’], ‘y’: -1*camera[‘y’], ‘z’: -1*camera[‘z’]}
|
Не достаточно просто определить, в каком направлении находится камера — вам также необходимо зафиксировать вращение камеры. Сделайте это путем определения вектора, перпендикулярного вектору cameraForward .
|
1
|
cameraPerpendicular = {‘x’: cameraForward[‘y’], ‘y’: -1*cameraForward[‘x’], ‘z’: 0}
|
1. Определите полезные векторные функции
Будет очень полезно иметь определенные векторные функции, определенные в нашей программе. Определите функцию векторной величины:
|
1
2
3
4
5
|
#magnitude of a 3D vector
def sumOfSquares(vector):
return vector[‘x’]**2 + vector[‘y’]**2 + vector[‘z’]**2
def magnitude(vector):
return math.sqrt(sumOfSquares(vector))
|
Нам нужно иметь возможность проецировать один вектор на другой. Поскольку эта операция включает в себя точечный продукт, гораздо проще использовать библиотеку NumPy. Однако NumPy принимает векторы в виде списка, без явных идентификаторов ‘x’, ‘y’, ‘z’, поэтому нам нужна функция для преобразования наших векторов в векторы NumPy.
|
1
2
3
|
#converts dictionary vector to list vector
def vectorToList (vector):
return [vector[‘x’], vector[‘y’], vector[‘z’]]
|
|
1
2
3
|
#projects u onto v
def vectorProject(u, v):
return np.dot(vectorToList (v), vectorToList (u))/magnitude(v)
|
Хорошо иметь функцию, которая даст нам единичный вектор в направлении заданного вектора:
|
1
2
3
4
|
#get unit vector
def unitVector(vector):
magVector = magnitude(vector)
return {‘x’: vector[‘x’]/magVector, ‘y’: vector[‘y’]/magVector, ‘z’: vector[‘z’]/magVector }
|
Наконец, нам нужно взять две точки и найти вектор между ними:
|
1
2
3
|
#Calculates vector from two points, dictionary form
def findVector (origin, point):
return { ‘x’: point[‘x’] — origin[‘x’], ‘y’: point[‘y’] — origin[‘y’], ‘z’: point[‘z’] — origin[‘z’] }
|
2. Определите оси камеры
Теперь нам нужно закончить определение осей камеры. У нас уже есть две из этих осей — cameraForward и cameraPerpendicular , соответствующие расстоянию z и координате x изображения камеры.
Теперь нам просто нужна третья ось, определяемая вектором, представляющим координату y изображения камеры. Мы можем найти эту третью ось, взяв перекрестное произведение этих двух векторов, используя NumPy — np.cross(vectorToList(cameraForward), vectorToList(cameraPerpendicular)) .
Первый элемент в результате соответствует компоненту x ; второй к компоненту y , и третий к компоненту z , таким образом, полученный вектор задается как:
|
1
2
|
#Calculates horizon plane vector (points upward)
cameraHorizon = {‘x’: np.cross(vectorToList(cameraForward) , vectorToList(cameraPerpendicular))[0], ‘y’: np.cross(vectorToList(cameraForward) , vectorToList(cameraPerpendicular))[1], ‘z’: np.cross(vectorToList(cameraForward) , vectorToList(cameraPerpendicular))[2] }
|
3. Проект ортогональный
Чтобы найти ортогональное расстояние x , y и z , сначала мы находим вектор, связывающий камеру и соответствующую точку, а затем проецируем его на каждую из трех осей камеры, определенных ранее:
|
1
2
3
4
|
def physicalProjection (point):
pointVector = findVector(camera, point)
#pointVector is a vector starting from the camera and ending at a point in question
return {‘x’: vectorProject(pointVector, cameraPerpendicular), ‘y’: vectorProject(pointVector, cameraHorizon), ‘z’: vectorProject(pointVector, cameraForward)}
|
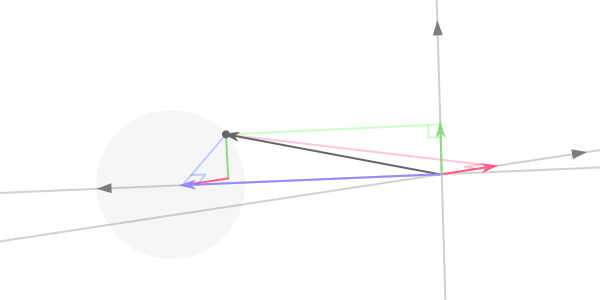
Точка (темно-серая), проецируемая на три оси камеры (серая). х красный, у зеленый, а г синий.
4. Проект на перспективу
Перспективная проекция просто берет x и y ортогональной проекции и делит каждую координату на расстояние z . Это делает так, чтобы вещи, которые находятся дальше, выглядели меньше, чем вещи, которые ближе к камере.
Поскольку деление на z дает очень маленькие координаты, мы умножаем каждую координату на значение, соответствующее фокусному расстоянию камеры.
|
1
|
focalLength = 1000
|
|
1
2
3
4
|
# draws points onto camera sensor using xDistance, yDistance, and zDistance
def perspectiveProjection (pCoords):
scaleFactor = focalLength/pCoords[‘z’]
return {‘x’: pCoords[‘x’]*scaleFactor, ‘y’: pCoords[‘y’]*scaleFactor}
|
5. Преобразуйте сферические координаты в прямоугольные координаты.
Земля — это сфера. Таким образом, наши координаты — широта и долгота — являются сферическими координатами. Итак, нам нужно написать функцию, которая преобразует сферические координаты в прямоугольные координаты (а также определяет радиус Земли и обеспечивает постоянную π ):
|
1
2
|
radius = 10
pi = 3.14159
|
|
1
2
3
|
#converts spherical coordinates to rectangular coordinates
def sphereToRect (r, a, b):
return {‘x’: r*math.sin(b*pi/180)*math.cos(a*pi/180), ‘y’: r*math.sin(b*pi/180)*math.sin(a*pi/180), ‘z’: r*math.cos(b*pi/180) }
|
Мы можем добиться лучшей производительности, сохраняя некоторые вычисления, использованные более одного раза:
|
1
2
3
4
5
6
|
#converts spherical coordinates to rectangular coordinates
def sphereToRect (r, a, b):
aRad = math.radians(a)
bRad = math.radians(b)
r_sin_b = r*math.sin(bRad)
return {‘x’: r_sin_b*math.cos(aRad), ‘y’: r_sin_b*math.sin(aRad), ‘z’: r*math.cos(bRad) }
|
Мы можем написать несколько составных функций, которые объединят все предыдущие шаги в одну функцию — переходя от сферических или прямоугольных координат к перспективным изображениям:
|
1
2
3
4
5
|
#functions for plotting points
def rectPlot (coordinate):
return perspectiveProjection(physicalProjection(coordinate))
def spherePlot (coordinate, sRadius):
return rectPlot(sphereToRect(sRadius, coordinate[‘long’], coordinate[‘lat’]))
|
4. Рендеринг в SVG
Наш скрипт должен иметь возможность записи в файл SVG. Так что начинать следует с:
|
1
2
|
f = open(‘globe.svg’, ‘w’)
f.write(‘<?xml version=\»1.0\» encoding=\»UTF-8\»?>\n<svg viewBox=»0 0 800 800″ version=»1.1″\nxmlns=»http://www.w3.org/2000/svg» xmlns:xlink=\»http://www.w3.org/1999/xlink\»>\n’)
|
И конец:
|
1
|
f.write(‘</svg>’)
|
Создание пустого, но действительного файла SVG. В этом файле сценарий должен иметь возможность создавать объекты SVG, поэтому мы определим две функции, которые позволят ему рисовать точки и полигоны SVG:
|
1
2
3
4
5
6
|
#Draws SVG circle object
def svgCircle (coordinate, circleRadius, color):
f.write(‘<circle cx=\»‘ + str(coordinate[‘x’] + 400) + ‘\» cy=\»‘ + str(coordinate[‘y’] + 400) + ‘\» r=\»‘ + str(circleRadius) + ‘\» style=\»fill:’ + color + ‘;\»/>\n’)
#Draws SVG polygon node
def polyNode (coordinate):
f.write(str(coordinate[‘x’] + 400) + ‘,’ + str(coordinate[‘y’] + 400) + ‘ ‘)
|
Мы можем проверить это, отрисовав сферическую сетку точек:
|
1
2
3
4
|
#DRAW GRID
for x in range(72):
for y in range(36):
svgCircle (spherePlot( { ‘long’: 5*x, ‘lat’: 5*y }, radius ), 1, ‘#ccc’)
|
Этот скрипт при сохранении и запуске должен выдать что-то вроде этого:

5. Преобразуйте данные карты SVG
Чтобы прочитать файл SVG, сценарий должен уметь читать файл XML, поскольку SVG — это тип XML. Вот почему мы импортировали xml.etree.ElementTree . Этот модуль позволяет вам загружать XML / SVG в скрипт как вложенный список:
|
1
2
|
tree = ET.parse(‘BlankMap Equirectangular states.svg’)
root = tree.getroot()
|
Вы можете перейти к объекту в SVG через индексы списка (обычно вам нужно взглянуть на исходный код файла карты, чтобы понять его структуру). В нашем случае каждая страна находится в root[4][0][ x ][ n ] , где x — номер страны, начиная с 1, а n — различные подпути, которые обозначают страну. Фактические контуры страны хранятся в атрибуте d , доступном через root[4][0][ x ][ n ].attrib['d'] .
1. Построить петли
Мы не можем просто перебрать эту карту, потому что в начале она содержит «фиктивный» элемент, который нужно пропустить. Таким образом, нам нужно посчитать количество «деревенских» объектов и вычесть один, чтобы избавиться от манекена. Затем мы перебираем оставшиеся объекты.
|
1
2
3
4
|
countries = len(root[4][0]) — 1
for x in range(countries):
root[4][0][x + 1]
|
Некоторые объекты страны включают несколько путей, поэтому мы затем выполняем итерацию по каждому пути в каждой стране:
|
1
2
3
4
|
countries = len(root[4][0]) — 1
for x in range(countries):
for path in root[4][0][x + 1]:
|
Внутри каждого пути есть непересекающиеся контуры, разделенные символами ‘Z M’ в строке d , поэтому мы разбиваем строку d вдоль этого разделителя и перебираем их .
|
1
2
3
4
5
|
countries = len(root[4][0]) — 1
for x in range(countries):
for path in root[4][0][x + 1]:
for k in re.split(‘Z M’, path.attrib[‘d’]):
|
Затем мы разделяем каждый контур по разделителям «Z», «L» или «M», чтобы получить координаты каждой точки на пути:
|
1
2
3
4
|
for x in range(countries):
for path in root[4][0][x + 1]:
for k in re.split(‘Z M’, path.attrib[‘d’]):
for i in re.split(‘Z|M|L’, k):
|
Затем мы удаляем все нечисловые символы из координат и разделяем их пополам вдоль запятых, указывая широту и долготу. Если оба существуют, мы сохраняем их в словаре sphereCoordinates (на карте координаты широты идут от 0 до 180 °, но мы хотим, чтобы они шли от –90 ° до 90 ° — на север и юг — поэтому мы вычитаем 90 °).
|
1
2
3
4
5
6
7
8
9
|
for x in range(countries):
for path in root[4][0][x + 1]:
for k in re.split(‘Z M’, path.attrib[‘d’]):
for i in re.split(‘Z|M|L’, k):
breakup = re.split(‘,’, re.sub(«[^-0123456789.,]», «», i))
if breakup[0] and breakup[1]:
sphereCoordinates = {}
sphereCoordinates[‘long’] = float(breakup[0])
sphereCoordinates[‘lat’] = float(breakup[1]) — 90
|
Затем, если мы проверим это путем построения некоторых точек ( svgCircle(spherePlot(sphereCoordinates, radius), 1, '#333') ), мы получим что-то вроде этого:

2. Решить для окклюзии
Это не делает различий между точками на ближней стороне земного шара и точками на дальней стороне земного шара. Если мы хотим просто напечатать точки на видимой стороне планеты, мы должны быть в состоянии выяснить, на какой стороне планеты находится данная точка.
Мы можем сделать это, вычислив две точки на сфере, где луч от камеры до точки будет пересекаться со сферой. Эта функция реализует формулу для решения расстояний до этих двух точек — dNear и dFar :
|
1
2
3
4
5
6
7
|
cameraDistanceSquare = sumOfSquares(camera)
#distance from globe center to camera
def distanceToPoint(spherePoint):
point = sphereToRect(radius, spherePoint[‘long’], spherePoint[‘lat’])
ray = findVector(camera,point)
return vectorProject(ray, cameraForward)
|
|
01
02
03
04
05
06
07
08
09
10
11
12
|
def occlude(spherePoint):
point = sphereToRect(radius, spherePoint[‘long’], spherePoint[‘lat’])
ray = findVector(camera,point)
d1 = magnitude(ray)
#distance from camera to point
dot_l = np.dot( [ray[‘x’]/d1, ray[‘y’]/d1, ray[‘z’]/d1], vectorToList(camera) )
#dot product of unit vector from camera to point and camera vector
determinant = math.sqrt(abs( (dot_l)**2 — cameraDistanceSquare + radius**2 ))
dNear = -(dot_l) + determinant
dFar = -(dot_l) — determinant
|
Если фактическое расстояние до точки d1 меньше или равно обоим этим расстояниям, то точка находится на ближней стороне сферы. Из-за ошибок округления в эту операцию встроена небольшая комната для маневра:
|
1
2
3
4
|
if d1 — 0.0000000001 <= dNear and d1 — 0.0000000001 <= dFar :
return True
else:
return False
|
Использование этой функции в качестве условия должно ограничивать рендеринг ближайшими боковыми точками:
|
1
2
|
if occlude(sphereCoordinates):
svgCircle(spherePlot(sphereCoordinates, radius), 1, ‘#333’)
|

6. Рендеринг твердых стран
Конечно, точки не являются действительно закрытыми, заполненными формами — они только создают иллюзию закрытых форм. Рисование реальных заполненных стран требует немного большей сложности. Прежде всего, нам нужно напечатать все видимые страны.
Мы можем сделать это, создав переключатель, который активируется в любое время, когда страна содержит видимую точку, в то же время временно сохраняя координаты этой страны. Если переключатель активирован, страна рисуется с использованием сохраненных координат. Мы также будем рисовать полигоны вместо точек.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
for x in range(countries):
for path in root[4][0][x + 1]:
for k in re.split(‘Z M’, path.attrib[‘d’]):
countryIsVisible = False
country = []
for i in re.split(‘Z|M|L’, k):
breakup = re.split(‘,’, re.sub(«[^-0123456789.,]», «», i))
if breakup[0] and breakup[1]:
sphereCoordinates = {}
sphereCoordinates[‘long’] = float(breakup[0])
sphereCoordinates[‘lat’] = float(breakup[1]) — 90
#DRAW COUNTRY
if occlude(sphereCoordinates):
country.append([sphereCoordinates, radius])
countryIsVisible = True
else:
country.append([sphereCoordinates, radius])
if countryIsVisible:
f.write(‘<polygon points=\»‘)
for i in country:
polyNode(spherePlot(i[0], i[1]))
f.write(‘\» style=»fill:#ff3092;stroke: #fff;stroke-width:0.3\» />\n\n’)
|

Трудно сказать, но страны на краю земного шара складываются в себя, чего мы не хотим (взгляните на Бразилию).
1. Трассировка диска Земли
Чтобы заставить страны правильно визуализироваться на краях земного шара, мы сначала должны проследить за диском земного шара с помощью многоугольника (диск, который вы видите из точек, является оптической иллюзией). Диск очерчен видимым краем шара — кругом. Следующие операции вычисляют радиус и центр этого круга, а также расстояние от плоскости, в которой находится круг от камеры, до центра шара.
|
1
2
3
4
5
6
7
8
9
|
#TRACE LIMB
limbRadius = math.sqrt( radius**2 — radius**4/cameraDistanceSquare )
cx = camera[‘x’]*radius**2/cameraDistanceSquare
cy = camera[‘y’]*radius**2/cameraDistanceSquare
cz = camera[‘z’]*radius**2/cameraDistanceSquare
planeDistance = magnitude(camera)*(1 — radius**2/cameraDistanceSquare)
planeDisplacement = math.sqrt(cx**2 + cy**2 + cz**2)
|
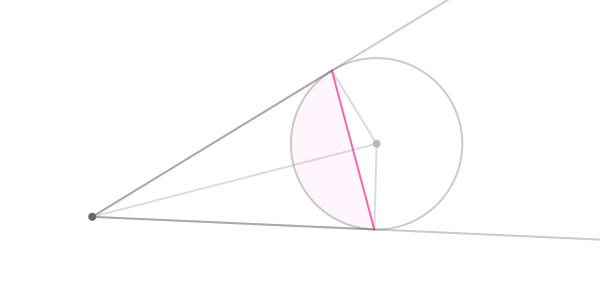
Земля и камера (темно-серая точка), вид сверху. Розовая линия представляет видимый край земли. Только заштрихованный сектор виден камере.
Затем, чтобы построить окружность в этой плоскости, построим две оси, параллельные этой плоскости:
|
1
2
3
4
|
#trade & negate x and y to get a perpendicular vector
unitVectorCamera = unitVector(camera)
aV = unitVector( {‘x’: -unitVectorCamera[‘y’], ‘y’: unitVectorCamera[‘x’], ‘z’: 0} )
bV = np.cross(vectorToList(aV), vectorToList( unitVectorCamera ))
|
Затем мы просто строим график на этих осях с шагом 2 градуса, чтобы построить окружность в этой плоскости с этим радиусом и центром (см. Это объяснение по математике):
|
1
2
3
4
5
6
|
for t in range(180):
theta = math.radians(2*t)
cosT = math.cos(theta)
sinT = math.sin(theta)
limbPoint = { ‘x’: cx + limbRadius*(cosT*aV[‘x’] + sinT*bV[0]), ‘y’: cy + limbRadius*(cosT*aV[‘y’] + sinT*bV[1]), ‘z’: cz + limbRadius*(cosT*aV[‘z’] + sinT*bV[2]) }
|
Затем мы просто инкапсулируем все это с помощью кода рисования многоугольника:
|
01
02
03
04
05
06
07
08
09
10
11
|
f.write(‘<polygon id=\»globe\» points=\»‘)
for t in range(180):
theta = math.radians(2*t)
cosT = math.cos(theta)
sinT = math.sin(theta)
limbPoint = { ‘x’: cx + limbRadius*(cosT*aV[‘x’] + sinT*bV[0]), ‘y’: cy + limbRadius*(cosT*aV[‘y’] + sinT*bV[1]), ‘z’: cz + limbRadius*(cosT*aV[‘z’] + sinT*bV[2]) }
polyNode(rectPlot(limbPoint))
f.write(‘\» style=»fill:#eee;stroke: none;stroke-width:0.5\» />’)
|
Мы также создаем копию этого объекта для последующего использования в качестве обтравочной маски для всех наших стран:
|
1
|
f.write(‘<clipPath id=\»clipglobe\»><use xlink:href=\»#globe\»/></clipPath>’)
|
Это должно дать вам это:

2. Отсечение на диск
Используя только что рассчитанный диск, мы можем изменить нашу инструкцию else в коде построения страны (когда координаты находятся на скрытой стороне земного шара), чтобы отобразить эти точки где-то за пределами диска:
|
1
2
3
4
|
else:
tangentscale = (radius + planeDisplacement)/(pi*0.5)
rr = 1 + abs(math.tan( (distanceToPoint(sphereCoordinates) — planeDistance)/tangentscale ))
country.append([sphereCoordinates, radius*rr])
|
Это использует касательную кривую, чтобы поднять скрытые точки над поверхностью Земли, создавая впечатление, что они распределены вокруг нее:

Это не совсем математический звук (он ломается, если камера не указана в центре планеты), но он прост и работает большую часть времени. Затем, просто добавив clip-path="url(#clipglobe)" в код рисования многоугольника, мы можем аккуратно обрезать страны до края земного шара:
|
1
2
|
if countryIsVisible:
f.write(‘<polygon clip-path=»url(#clipglobe)» points=\»‘)
|

Я надеюсь, вам понравился этот урок! Удачи с вашими векторными шарами!
