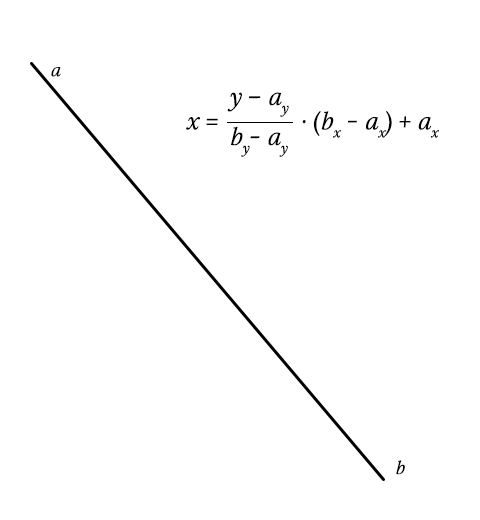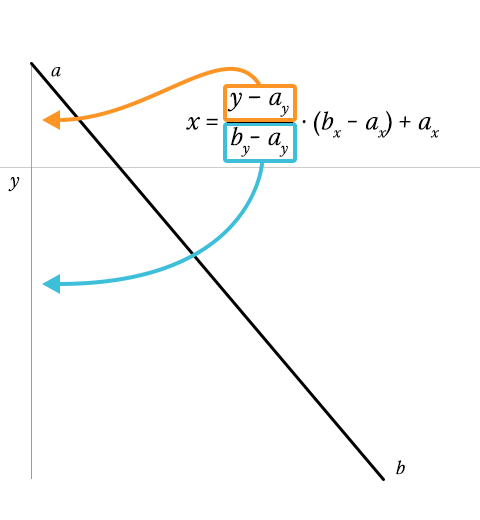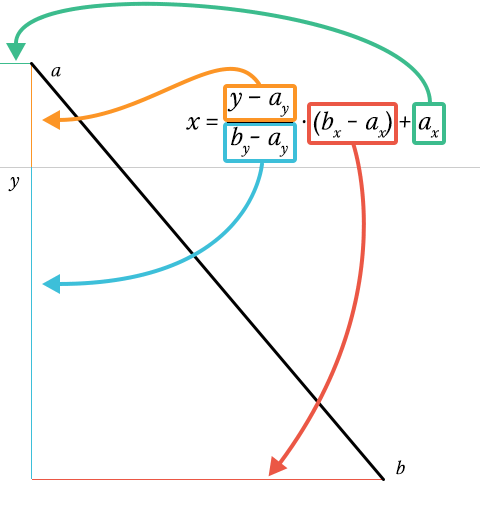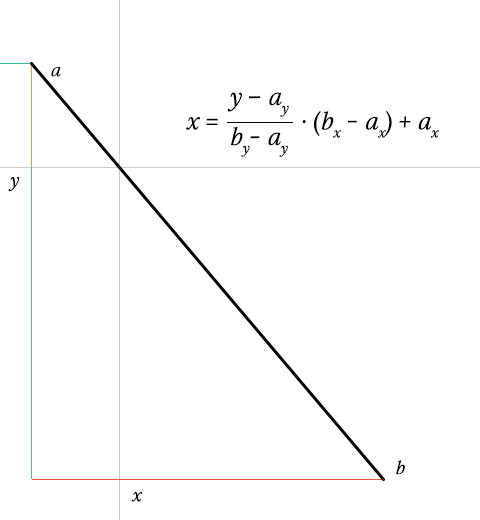Статьи

Векторная графика в Sass

Декабрь 5, 2018

Sass — очень мощный инструмент, и многие из нас все еще изучают его ограничения. Что мы можем сделать с этим и как далеко мы можем продвинуть это?

После того, как я бросил идеи в Уго Жирауделя , я был очень взволнован одной идеей; 2D графический движок. Это может сбивать с толку, потому что CSS и, следовательно, Sass уже являются частью графической области. Вместо того, чтобы стилизовать контент, я хотел (ab) использовать Sass для рендеринга изображения, пиксель за пикселем. Вывод может быть нарисован как значение box-shadow для элемента пикселя 1 × 1.

Изучение стратегий

Одним из способов является итерация по сетке и списку объектов и проверка необходимости рисования пикселя. Sass должен был бы обработать n x width x height итераций, где n — количество объектов. Это большая работа, поэтому не очень производительная, особенно учитывая, что циклы в Sass не быстрые. Вместо визуализации всей сетки можно отобразить только те части, которые могут содержать объект, получив так называемый ограничивающий прямоугольник. Проверьте демо .

Лучшим вариантом является использование путей.

Пути могут показаться вам знакомыми. Это общий термин в графических программах, таких как Adobe Illustrator и Adobe Photoshop, но он встречается и в таких веб-технологиях, как SVG и HTML5. Путь — это список координат, которые соединены последовательно. Все, что мне нужно, чтобы определить форму, это пара координат. Если вы знакомы с путями, вы, вероятно, знаете, что вы также можете делать изогнутые пути. А пока я буду придерживаться прямых линий.

Процесс преобразования векторного пути в пиксели — или, в нашем случае, векторный путь — в тень блока — называется растеризацией .

Алгоритм Scanline

Пути часто отображаются с использованием алгоритма сканирования линии. Лично, всякий раз, когда я слышу слово «алгоритм», я паникую и выполняю любую стратегию выхода, которая у меня есть под рукой. Однако этот алгоритм удивительно понятен, так что пока не пугайтесь!

Перебираем вертикальные пиксели. Для каждой строки мы храним пересечения всех линий этого пути. После перебора всех линий мы сортируем и пересекаем пересечения слева направо. На каждом перекрестке мы переключаем рисунок.

Алгоритм сканирования

Sass реализация

Перед рендерингом полезно знать, что делать. Мы должны определить путь. Я думаю, что список координат является довольно хорошей настройкой: 

$square: (
  (0, 0), (64, 0),
  (64, 64), (0, 64)
);

Их можно легко масштабировать и переводить (перемещать): 

 @function scale($path, $scale) {
  @for $n from 1 through length($path) {
    $coords: nth($path, $n);

    $path: set-nth($path, $n, (
      nth($coords, 1) * $scale,
      nth($coords, 2) * $scale
    ));
  }

  @return $path;
}

@function translate($path, $x, $y) {
  @for $n from 1 through length($path) {
    $coords: nth($path, $n);

    $path: set-nth($path, $n, (
      nth($coords, 1) + $x,
      nth($coords, 2) + $y
    ));
  }

  @return $path;
}

Чтобы отобразить определенный цвет, мы можем захотеть передать цвет функции, которая выведет список теней, например: 

 $shadows: ();

// Append more shadows
$shadows: render($shadows, $square, #f00);

В нашей функции render() Это схема render() 

 @function render($list, $path, $color) {
  // List to store shadows
  $shadows: ();

  // Do a lot of thinking

  @if length($shadows) > 0 {
    @return append($list, $shadows, comma);
  }

  @return $shadows;
}

Чтобы вычислить площадь, которую мы должны нарисовать, мы можем перебрать все координаты пути и сохранить минимальное и максимальное значение на оси Y. Таким образом, мы знаем, где начать и остановить рисование на оси Y. Знание того, что нужно визуализировать на оси X, будет вычислено с использованием линий пути, которые будут рассмотрены в ближайшее время. 

 // Initial values
$top: null;
$bottom: null;

@each $coord in $path {
    $y: nth($coord, 2);

    // @if $top is still null, let's set current value
    // @else get the smaller value between previous y and current y
    @if $top == null { $top: $y; }
    @else { $top: min($y, $top); }

    // Same thing for the bottom, but get the largest value instead
    @if $bottom == null { $bottom: $y; }
    @else { $bottom: max($y, $bottom); }
}

Зная вертикальную границу пути, мы можем перебирать строки и использовать это для вычисления пересечений линий пути. Пересечения затем сортируются, чтобы убедиться, что рисунок сделан правильно. Мы рассмотрим логику рисования позже. 

 // If there is something to draw at all
@if $bottom - $top > 0 {
  // Iterate through rows
  @for $y from $top through $bottom {
    // Get intersections
    $intersections: intersections($path, $y);

    @if type-of($intersections) == 'list' and length($intersections) > 0 {
        $intersections: quick-sort($intersections, 'compare');

        // Drawing logic
      }
    }
  }
}

Функция intersections($path, $y) Схема довольно проста. Мы перебираем путь, и для каждой строки ищем пересечения. Наконец, мы возвращаем список этих пересечений. 

 @function intersections($path, $y) {
  $intersections: ();
  $length: length($path);

  // Iterate through path
  @for $n from 1 through $length {
    // Intersection algorithm here
  }

  @return $intersections;
}

Время для Sass-паузы. Получить пересечение линии сложно. Получив высоту линии ( b y — a y ), мы можем определить продвижение y по высоте ( y — a y / height ). Это должно быть число от 0 до 1. Если нет, y вообще не пересекается с линией.

Поскольку линии являются линейными, мы можем умножить это число на ширину линии ( b x — a x ), поэтому мы получаем координату x относительно положения линии. Все, что осталось, это добавить горизонтальную позицию линии (… + a x ), и мы получим нашу окончательную координату x!

Sass Векторная графика Математика

Вернуться к Sass. Давайте реализуем вышеизложенное: 

 // Get current and next point in this path, which makes a line
$a: nth($path, $n);
$b: nth($path, ($n % $length) + 1);

// Get boundaries of this line
$top: min(nth($a, 2), nth($b, 2));
$bottom: max(nth($a, 2), nth($b, 2));

// Get size of the line
$height: nth($b, 2) - nth($a, 2);
$width: nth($b, 1) - nth($a, 1);

// Is line within boundaries?
@if $y >= $top and $y <= $bottom and $height != 0 {
  // Get intersection at $y and add it to the list
  $x: ($y - nth($a, 2)) / $height * $width + nth($a, 1);
  $intersections: append($intersections, $x);
}

Что касается логики рисования, мы можем взглянуть на первую анимацию, которая демонстрирует алгоритм линии сканирования. Как видите, он рисует пересечение 1 к 2, 3 к 4 и т. Д.

Для каждого пересечения мы переключаем рисунок. Затем мы просто заполняем пиксели в $shadows 

 // Boolean to decide whether to draw or not
$draw: false;

// Iterate through intersections
@for $n from 1 through length($intersections) {
  // To draw or not to draw?
  $draw: not $draw;

  // Should we draw?
  @if $draw {
    // Get current and next intersection
    $current: nth($intersections, $n);
    $next: nth($intersections, $n + 1);

    // Get x coordinates of our intersections
    $from: round($current);
    $to: round($next);

    // Draw the line between the x coordinates
    @for $x from $from through $to {
      $value: ($x + 0px) ($y + 0px) $color;
      $shadows: append($shadows, $value, comma);
    }
  }
}

Вывод

Давайте взглянем назад на то, что, черт возьми, только что произошло:

  1. Определите путь
  2. Создать ограничивающую рамку пути
  3. Итерация по оси Y ограничительной рамки
  4. Получить пересечения всех линий в пути
  5. Сортировать пересечения по координате х
  6. Итерация через пересечения
  7. Для каждого нечетного пересечения, рисовать до следующего
  8. Магия выхода

Смотрите демо (и полный код)

Так что-нибудь из этого полезно? Не удаленно. Производительность действительно очень плохая. Рисование некоторых основных объектов занимает несколько минут. LibSass, однако, делает его менее болезненным, возможно, даже терпимым. Но кого мы шутим, верно? Если вы намереваетесь отображать векторные пути, придерживайтесь SVG или элемента Canvas или даже WebGL. Все это делает растеризацию для вас, и вы получаете гораздо больше возможностей и повышаете производительность.

Однако это доказывает, что Sass довольно мощный, и мы можем делать с ним сумасшедшие забавные вещи. Любое приложение, которое может быть написано на Sass, в конечном итоге будет написано на Sass .

35
Share: