Эта статья была рецензирована Тимом Севериеном и Саймоном Кодрингтоном . Спасибо всем рецензентам SitePoint за то, что сделали контент SitePoint как можно лучше!
Отображать изображения и другие плоские формы на веб-страницах довольно просто. Однако, когда дело доходит до отображения 3D-фигур, все становится не так просто, поскольку 3D-геометрия более сложна, чем 2D-геометрия. Для этого вы можете использовать специальные технологии и библиотеки, например, WebGL и Three.js .
Однако эти технологии не нужны, если вы просто хотите отобразить некоторые базовые фигуры, например, куб. Более того, они не помогут вам понять, как они работают и как мы можем отображать 3D-фигуры на плоском экране.
Цель этого руководства — объяснить, как мы можем создать простой 3D-движок для Интернета без WebGL. Сначала мы увидим, как мы можем хранить трехмерные фигуры. Затем мы увидим, как отображать эти фигуры в двух разных видах.
Хранение и Преобразование 3D-фигур
Все формы многогранники
Виртуальный мир отличается от реального одним главным образом: ничто не является непрерывным, и все является дискретным. Например, вы не можете отобразить идеальный круг на экране. Вы можете подойти к нему, нарисовав правильный многоугольник с большим количеством ребер: чем больше у вас ребер, тем более «идеальным» будет ваш круг.
В 3D это то же самое, и к каждой фигуре нужно подходить с помощью трехмерного эквивалента многоугольника: многогранник (трехмерная фигура, в которой мы находим только плоские грани и не изогнутые стороны, как в сфере). Это не удивительно, когда мы говорим о фигуре, которая уже является многогранником, например, кубом, но об этом следует помнить, когда мы хотим отобразить другие фигуры, например сферу.
Хранение многогранника
Чтобы угадать, как хранить многогранник, мы должны помнить, как такая вещь может быть идентифицирована в математике. Вы, конечно, уже сделали некоторые базовые геометрии в школьные годы. Например, чтобы идентифицировать квадрат, вы называете его ABCDABCD
Для нашего 3D движка это будет то же самое. Мы начнем с сохранения каждой вершины нашей фигуры. Затем эта фигура будет перечислять свои грани, а каждая грань будет перечислять свои вершины.
Чтобы представить вершину, нам нужна правильная структура. Здесь мы создаем класс для хранения координат вершины.
var Vertex = function(x, y, z) {
this.x = parseFloat(x);
this.y = parseFloat(y);
this.z = parseFloat(z);
};
Теперь вершина может быть создана как любой другой объект:
var A = new Vertex(10, 20, 0.5);
Далее мы создаем класс, представляющий наш многогранник. Давайте возьмем куб в качестве примера. Определение класса ниже, с объяснением сразу после.
var Cube = function(center, size) {
// Generate the vertices
var d = size / 2;
this.vertices = [
new Vertex(center.x - d, center.y - d, center.z + d),
new Vertex(center.x - d, center.y - d, center.z - d),
new Vertex(center.x + d, center.y - d, center.z - d),
new Vertex(center.x + d, center.y - d, center.z + d),
new Vertex(center.x + d, center.y + d, center.z + d),
new Vertex(center.x + d, center.y + d, center.z - d),
new Vertex(center.x - d, center.y + d, center.z - d),
new Vertex(center.x - d, center.y + d, center.z + d)
];
// Generate the faces
this.faces = [
[this.vertices[0], this.vertices[1], this.vertices[2], this.vertices[3]],
[this.vertices[3], this.vertices[2], this.vertices[5], this.vertices[4]],
[this.vertices[4], this.vertices[5], this.vertices[6], this.vertices[7]],
[this.vertices[7], this.vertices[6], this.vertices[1], this.vertices[0]],
[this.vertices[7], this.vertices[0], this.vertices[3], this.vertices[4]],
[this.vertices[1], this.vertices[6], this.vertices[5], this.vertices[2]]
];
};
Используя этот класс, мы можем создать виртуальный куб, указав его центр и длину его ребер.
var cube = new Cube(new Vertex(0, 0, 0), 200);
Конструктор класса Cube Схема будет более понятной, поэтому посмотрите ниже положения восьми сгенерированных нами вершин:
Затем мы перечисляем лица. Каждое лицо является квадратом, поэтому нам нужно указать четыре вершины для каждого лица. Здесь я решил представить лицо с массивом, но, если вам нужно, вы можете создать выделенный класс для этого.
Когда мы создаем лицо, мы используем четыре вершины. Нам не нужно снова указывать их положение, так как они хранятся в this.vertices[i] Это практично, но есть и другая причина, по которой мы это сделали.
По умолчанию JavaScript пытается использовать минимально возможный объем памяти. Для этого он не копирует объекты, которые передаются в качестве аргументов функций или даже хранятся в массивах. Для нашего случая это идеальное поведение.
Фактически, каждая вершина содержит три числа (их координаты) плюс несколько методов, если нам нужно добавить их. Если для каждого лица мы сохраняем копию вершины, мы будем использовать много памяти, что бесполезно. Здесь все, что у нас есть, это ссылки: координаты (и другие методы) сохраняются один раз и только один раз. Поскольку каждая вершина используется тремя разными гранями, сохраняя ссылки, а не копии, мы делим требуемую память на три (более или менее)!
Нужны ли нам треугольники?
Если вы уже играли с 3D (с программным обеспечением, например, Blender, или с библиотеками, такими как WebGL), возможно, вы слышали, что мы должны использовать треугольники. Здесь я решил не использовать треугольники.
Причиной такого выбора является то, что эта статья является введением в тему, и мы будем отображать основные фигуры, такие как кубики. Использование треугольников для отображения квадратов было бы более сложным, чем что-либо еще в нашем случае.
Однако, если вы планируете построить более полный рендерер, вам нужно знать, что, как правило, треугольники предпочтительнее. Для этого есть две основные причины:
- Текстуры: для отображения изображений на лицах нам нужны треугольники по некоторым математическим причинам;
- Странные лица: три вершины всегда находятся в одной плоскости. Однако вы можете добавить четвертую вершину, которая не находится в той же плоскости, и вы можете создать грань, соединяющую эти четыре вершины. В таком случае, чтобы нарисовать его, у нас нет выбора: мы должны разделить его на два треугольника (просто попробуйте с листом бумаги!). Используя треугольники, вы сохраняете контроль и выбираете, где происходит разделение (спасибо Тиму за напоминание!).
Действуя на многогранник
Есть еще одно преимущество в хранении ссылок вместо копий. Когда мы хотим изменить многогранник, использование такой системы также разделит необходимое количество операций на три.
Чтобы понять почему, давайте еще раз вспомним наш урок математики. Когда вы хотите перевести квадрат, вы на самом деле не переводите его. Фактически, вы переводите четыре вершины и присоединяетесь к переводам.
Здесь мы сделаем то же самое: мы не будем касаться лиц. Мы применяем требуемую операцию к каждой вершине, и все готово. Поскольку лица используют ссылки, координаты лиц автоматически обновляются. Например, посмотрите, как мы можем перевести наш ранее созданный куб:
for (var i = 0; i < 8; ++i) {
cube.vertices[i].x += 50;
cube.vertices[i].y += 20;
cube.vertices[i].z += 15;
}
Рендеринг изображения
Мы знаем, как хранить трехмерные объекты и как действовать на них. Теперь пришло время посмотреть, как их посмотреть! Но сначала нам нужен небольшой фон в теории, чтобы понять, что мы собираемся делать.
проекция
В настоящее время мы храним 3D-координаты. Тем не менее, экран может отображать только 2D-координаты, поэтому нам нужен способ преобразовать наши 3D-координаты в 2D: это то, что мы называем проекцией в математике. 3D-2D-проекция — это абстрактная операция, выполняемая новым объектом, который называется виртуальной камерой. Эта камера берет трехмерный объект и преобразует его координаты в двухмерные, чтобы отправить их рендереру, который отобразит их на экране. Здесь мы будем предполагать, что наша камера находится в начале нашего трехмерного пространства (поэтому ее координаты (0,0,0)
С начала этой статьи мы говорили о координатах, представленных тремя числами: xyz Но чтобы определить координаты, нам нужен базис: является ли z Это идет вверх или вниз? Нет универсального ответа и нет соглашения, поскольку факт заключается в том, что вы можете выбирать все, что хотите. Единственное, что вы должны иметь в виду, это то, что при работе с трехмерными объектами вы должны быть последовательными, так как формулы будут меняться в зависимости от этого. В этой статье я выбрал основу, которую вы можете видеть на схеме куба выше: xyz
Теперь мы знаем, что делать: у нас есть координаты в базисе (x,y,z)(x,z)
Там не только одна проекция. Хуже того, существует бесконечное количество разных проекций! В этой статье мы увидим два разных типа проекций, которые на практике являются наиболее используемыми.
Как сделать нашу сцену
Прежде чем проецировать наши объекты, давайте напишем функцию, которая будет их отображать. Эта функция принимает в качестве параметров массив, перечисляющий объекты для визуализации, контекст холста, который должен использоваться для отображения объектов, и другие детали, необходимые для рисования объектов в нужном месте.
Массив может содержать несколько объектов для рендеринга. Эти объекты должны учитывать одну вещь: иметь открытое свойство с именем faces Эти грани могут быть любыми (квадрат, треугольник или даже додекагон, если хотите): они просто должны быть массивами, перечисляющими их вершины.
Давайте посмотрим на код функции, а затем объяснение:
function render(objects, ctx, dx, dy) {
// For each object
for (var i = 0, n_obj = objects.length; i < n_obj; ++i) {
// For each face
for (var j = 0, n_faces = objects[i].faces.length; j < n_faces; ++j) {
// Current face
var face = objects[i].faces[j];
// Draw the first vertex
var P = project(face[0]);
ctx.beginPath();
ctx.moveTo(P.x + dx, -P.y + dy);
// Draw the other vertices
for (var k = 1, n_vertices = face.length; k < n_vertices; ++k) {
P = project(face[k]);
ctx.lineTo(P.x + dx, -P.y + dy);
}
// Close the path and draw the face
ctx.closePath();
ctx.stroke();
ctx.fill();
}
}
}
Эта функция заслуживает некоторого объяснения. Точнее нам нужно объяснить, что это за функция project()dxdy Все остальное — это не что иное, как перечисление объектов, затем рисование каждого лица.
Как следует из названия, функция project() Он принимает вершину в 3D-пространстве и возвращает вершину в 2D-плоскости, которую мы могли бы определить, как показано ниже.
var Vertex2D = function(x, y) {
this.x = parseFloat(x);
this.y = parseFloat(y);
};
Вместо того, чтобы называть координаты xzzyz
Точное содержание project() Но каким бы ни был этот тип, функцию render()
Как только у нас есть координаты на плоскости, мы можем отобразить их на холсте, и вот что мы делаем … с небольшой хитростью: мы на самом деле не рисуем фактические координаты, возвращаемые функцией project()
Фактически, функция project() Однако мы хотим, чтобы начало координат было в центре нашего холста, поэтому мы переводим координаты: вершина (0,0)(0 + dx,0 + dy)dxdy Поскольку мы хотим, чтобы (dx,dy)dx = canvas.width / 2dy = canvas.height / 2
Наконец, последняя деталь: почему мы используем -yy Ответ в нашем выборе базы: ось z Тогда в нашей сцене вершина с положительной координатой z будет двигаться вверх. Однако на холсте ось y Вот почему нам нужно определить координату y холста на холсте как обратную координату z нашей сцены.
Теперь, когда функция render()project()
Ортогональный вид
Начнем с ортографической проекции. Как проще всего, это прекрасно, чтобы понять, что мы будем делать.
У нас есть три координаты, и мы хотим только две. Что проще всего сделать в таком случае? Удалить одну из координат. И это то, что мы делаем с точки зрения орфографии. Мы удалим координату, которая представляет глубину: координата y
function project(M) {
return new Vertex2D(M.x, M.z);
}
Теперь вы можете протестировать весь код, который мы написали с начала этой статьи: он работает! Поздравляем, вы только что отобразили 3D объект на плоском экране!
Эта функция реализована в приведенном ниже примере, где вы можете взаимодействовать с кубом, вращая его с помощью мыши.
Иногда мы хотим получить орфографическое представление, поскольку оно имеет преимущество сохранения параллелей. Однако это не самый естественный вид: наши глаза не видят так. Вот почему мы увидим второй прогноз: перспективный вид.
Перспективный вид
Перспективный вид немного сложнее, чем ортографический, так как нам нужно сделать некоторые вычисления. Однако эти вычисления не так сложны, и вам нужно знать только одно: как использовать теорему о перехвате .
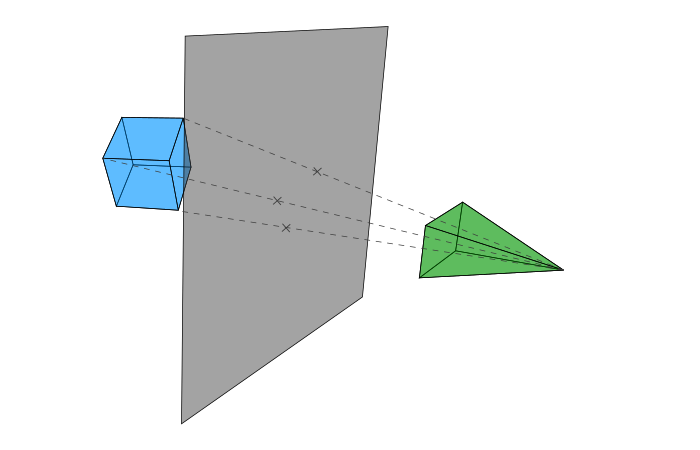
Чтобы понять почему, давайте посмотрим на схему, представляющую орфографический вид. Мы спроецировали наши точки на плоскость ортогональным способом.
Но в реальной жизни наши глаза больше похожи на следующую схему.
По сути, у нас есть два шага:
- Мы соединяем исходную вершину и происхождение камеры;
- Проекция — это пересечение этой линии и плоскости.
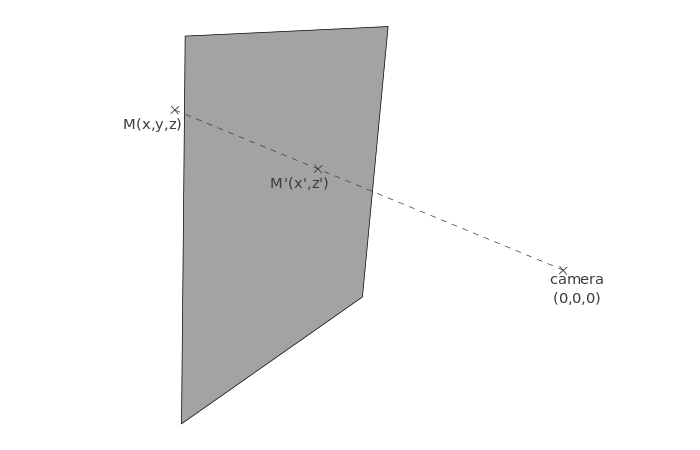
Вопреки ортографическому виду, точное местоположение плоскости здесь важно: если вы разместите плоскость далеко от камеры, вы не получите тот же эффект, что и если расположите ее близко к ней. Здесь мы размещаем его на расстоянии d
Начиная с вершины M(x,y,z)(x',z')M'
Чтобы угадать, как мы будем вычислять эти координаты, давайте возьмем другую точку зрения и увидим ту же схему, что и выше, но видимую сверху.
Мы можем распознать конфигурацию, используемую в теореме о перехвате. На схеме выше мы знаем некоторые значения: xyd Мы хотим вычислить x'x' = d / y * x
Теперь, если вы посмотрите на ту же сцену со стороны, вы получите похожую схему, позволяющую вам получить значение z'zydz' = d / y * z
Теперь мы можем написать функцию project()
function project(M) {
// Distance between the camera and the plane
var d = 200;
var r = d / M.y;
return new Vertex2D(r * M.x, r * M.z);
}
Эта функция может быть протестирована в следующем примере. Еще раз, вы можете взаимодействовать с кубом.
Заключительные слова
Наш (очень простой) 3D-движок теперь готов отображать любую трехмерную фигуру, которую мы хотим. Есть несколько вещей, которые вы можете сделать, чтобы улучшить его. Например, мы видим каждое лицо наших фигур, даже те, что сзади. Чтобы спрятать их, вы можете выполнить выборку на задней панели .
Также мы не говорили о текстурах. Здесь все наши формы имеют одинаковый цвет. Вы можете изменить это, например, добавив свойство color Вы даже можете выбрать один цвет для лица, не меняя много вещей. Вы также можете попробовать отобразить изображения на лицах. Тем не менее, это сложнее, и подробное описание того, как это сделать, займет целую статью.
Другие вещи могут быть изменены. Мы поместили камеру в начало пространства, но вы можете переместить ее (перед проецированием вершин потребуется смена базиса). Также здесь нарисованы вершины, расположенные за камерой, и это не то, чего мы хотим. План отсечения может исправить это (легко понять, менее легко реализовать).
Как вы видите, 3D-движок, который мы здесь создали, далек от завершения, и это также моя собственная интерпретация. Вы можете добавить свой собственный контакт с другими классами: например, Three.js использует специальный класс для управления камерой и проекцией. Кроме того, мы использовали базовую математику для хранения координат, но если вы хотите создать более сложное приложение и если вам нужно, например, вращать много вершин во время кадра, у вас не будет гладкого опыта. Чтобы оптимизировать его, вам понадобится более сложная математика: однородные координаты (проективная геометрия) и кватернионы .
Если у вас есть идеи для ваших собственных улучшений движка, или вы создали что-то классное на основе этого кода, пожалуйста, дайте мне знать в комментариях ниже!