В предыдущих быстрых советах мы рассматривали обнаружение столкновений: по сути, обнаружение того, что две фигуры перекрываются. Теперь мы готовы взглянуть на реакцию на столкновение: заставить что-то произойти из-за столкновения. В этом кратком совете мы рассмотрим реакции отражения и скольжения.
Окончательный результат предварительного просмотра
Давайте посмотрим на конечный результат, которого мы достигнем в конце этого урока. Каждая демонстрация Flash имеет кнопку перезапуска; щелкните по нему, чтобы сбросить положение кругов в верхней части сцены.
Первая демонстрация демонстрирует отражение :
Второе показывает скольжение :
Шаг 1: формула отражения
Я изучал эту тему несколько раундов со студентами, и опыт научил меня, что непосредственный подход к объяснению векторной математики для новичков приводит к пустым лицам и смущенному уму. Поэтому вместо того, чтобы читать здесь лекцию по математике, я отошлю тех, кто заинтересован в изучении этой темы, к странице Вольфрама о размышлении .
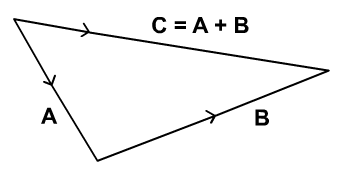
Здесь я упрощу свои объяснения с диаграммами ниже. Напомним вектор сложения:
Теперь посмотрите на диаграмму ниже. A — это скорость круга до столкновения, а A ‘- его скорость после столкновения.
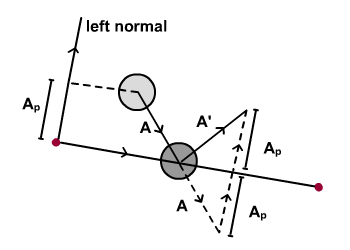
Очевидно, что A' = A + 2 V(A p ) , где V(A p ) представляет вектор с величиной A p в направлении левой нормали. (Вы можете увидеть это, следуя пунктирным линиям.)
Чтобы получить V(A p ) , спроецируем A на левую нормаль.
Шаг 2: Реализация
Здесь идет реализация отражения в ActionScript. Я выделил важные части. Строка 67 — 69 предназначена для вычисления V(A p ) ( v_leftNormSeg2 ), а строка 70 реализует формулу. Вы можете обратиться к полному ActionScript под Reaction1.as.
(Вы должны распознать большую часть кода из предыдущего Быстрого совета .)
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
private function refresh(e:Event):void {
for (var i:int = 0; i < circles.length; i++) {
//calculating line’s perpendicular distance to ball
var c1_circle:Vector2D = new Vector2D(circles[i].x — x1, circles[i].y — y1);
var c1_circle_onNormal:Number = c1_circle.projectionOn(leftNormal);
var c1_circle_onLine:Number = c1_circle.projectionOn(line);
//if collision happened, undo movement
if (Math.abs(c1_circle_onNormal) <= circles[i].radius
&& line.dotProduct(c1_circle) > 0
&& c1_circle_onLine < line.getMagnitude()){
//redefine velocity
var v_leftNormSeg2:Vector2D = leftNormal.clone();
var leftNormSeg2_mag:Number = Math.abs(velos[i].projectionOn(leftNormal))
v_leftNormSeg2.setMagnitude(leftNormSeg2_mag);
velos[i] = velos[i].add(v_leftNormSeg2.multiply(2));
}
circles[i].x += velos[i].x;
circles[i].y += velos[i].y;
}
}
|
Шаг 3: Интерактивная версия
Обратите внимание, что эта формула отражения применима к линии любого градиента. Фактически, вы можете запрограммировать вашу линию так, чтобы она была настраиваемой во время выполнения, и чтобы она отображала круги, подобные представленной ниже презентации Flash. Просто нажмите и перетащите возле нижнего края, чтобы переопределить его.
Шаг 4: скользя по линии
Концепция скольжения вдоль линии почти идентична отражению. Соблюдайте схему ниже.
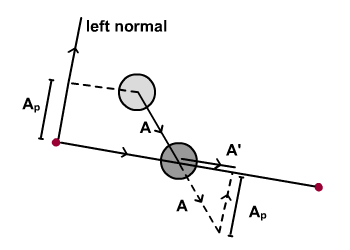
Вектор слайда A' = A + V(A p ) где V(A p ) представляет вектор с величиной A p . Снова, чтобы получить A p, мы спроецируем A на левую нормаль.
Обратите внимание, что, поскольку круг скользит вдоль линии, он сталкивается с линией. Конечно, точки столкновения различаются между кругами, которые сталкиваются на линии, поэтому некоторые из них перекрывают линию, когда они движутся вдоль нее. Это выглядит не очень хорошо, поэтому нам придется изменить их положение.
Шаг 5: переопределить местоположение
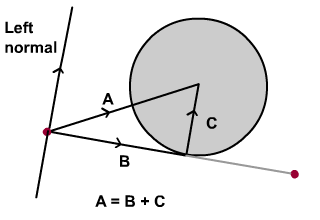
Теперь давайте переместим круги на линии, сохраняя их контакт с линией. Обратитесь к диаграмме ниже.
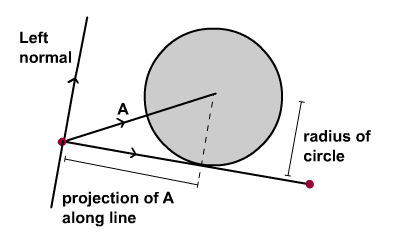
Важной переменной для расчета является проекция А вдоль линии. Радиус круга легко доступен, и у нас уже есть B, так что мы можем сформировать векторы B и C. Добавление двух даст нам A, точное местоположение для изменения положения круга. Просто!
Флеш-презентация ниже кодируется в соответствии с упомянутой идеей. Но есть одна проблема: круги дрожат вдоль линии.
Есть одна последняя деталь, которую мы пропустили. Диаграмма выше показывает, что величина C должна быть эквивалентна радиусу круга. Тем не менее, это поместит круг обратно над линией. Поскольку там не обнаружено столкновений, круг снова упадет на линию, что, в свою очередь, помечает обнаружение столкновений и вызывает перемещение круга.
Этот цикл будет повторяться до конца сегмента линии; визуальный результат этого цикла — эффект дрожания.
Решение этой проблемы состоит в том, чтобы установить величину C немного меньше радиуса круга: (radius of circle - 1) , скажем. Посмотрите демонстрацию Flash ниже, которая использует эту идею:
Шаг 6: Реализация
Итак, вот важный фрагмент ActionScript для скольжения по линии. Я выделил важные части.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
private function refresh(e:Event):void {
for (var i:int = 0; i < circles.length; i++) {
//calculating line’s perpendicular distance to ball
var c1_circle:Vector2D = new Vector2D(circles[i].x — x1, circles[i].y — y1);
var c1_circle_onNormal:Number = c1_circle.projectionOn(leftNormal);
var c1_circle_onLine:Number = c1_circle.projectionOn(line);
//check for collision
if (Math.abs(c1_circle_onNormal) <= circles[i].radius){
//check if within segment
//if within segment, reposition and recalculate velocity
if (line.dotProduct(c1_circle) > 0 && c1_circle_onLine < line.getMagnitude()) {
//repostion circle
var v_lineSeg:Vector2D = line.clone();
v_lineSeg.setMagnitude(c1_circle_onLine);
var v_leftNormSeg1:Vector2D = leftNormal.clone();
v_leftNormSeg1.setMagnitude(circles[i].radius — 1);
//v_leftNormSeg1.setMagnitude(circles[i].radius);
var reposition:Vector2D = v_lineSeg.add(v_leftNormSeg1)
circles[i].x = x1+reposition.x;
circles[i].y = y1+reposition.y;
//redefine velocity
var v_leftNormSeg2:Vector2D = leftNormal.clone();
var leftNormSeg2_mag:Number = Math.abs(velos[i].projectionOn(leftNormal))
v_leftNormSeg2.setMagnitude(leftNormSeg2_mag);
var veloAlongLine:Vector2D = velos[i].add(v_leftNormSeg2);
circles[i].x += veloAlongLine.x;
circles[i].y += veloAlongLine.y;
}
//if not in segment (eg slide out of segment), continue to fall down
else {
circles[i].x += velos[i].x;
circles[i].y += velos[i].y;
}
}
//No collision in the first place, fall down
else {
circles[i].x += velos[i].x;
circles[i].y += velos[i].y;
}
}
}
|
Вывод
Надеюсь, это полезно. Спасибо за прочтение. Подскажите мне, если есть вопросы, и увидимся в следующем кратком совете.