В моем предыдущем кратком совете мы рассмотрели идею обнаружения столкновений в целом и, в частности, обнаружение столкновений между парой окружностей. В этом кратком совете мы рассмотрим обнаружение столкновения между кругом и линией.
Это результат, над которым мы будем работать. Нажмите кнопку «Перезагрузить», чтобы переместить все круги в верхней части сцены и посмотреть, как они падают.
Обратите внимание, что круги сталкиваются с линией даже вне нарисованного отрезка. Мой следующий быстрый совет покажет, как это исправить.
Шаг 1: Общая идея
Чтобы проверить, столкнулся ли какой-либо круг с линией, мы должны проверить перпендикулярную длину от линии до круга. Соблюдайте схему ниже.
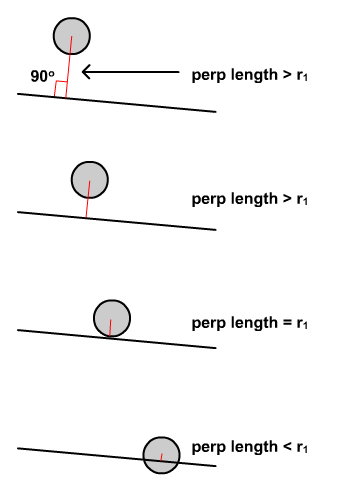
Из диаграммы выше видно, что случаи 3 и 4 должны обнаруживать столкновение между окружностью и линией. Таким образом, мы заключаем, что, если длина перпендикуляра (отмечена красным) равна или меньше радиуса круга, столкновение произошло из-за того, что круг коснулся или перекрыл линию. Вопрос в том, как рассчитать эту перпендикулярную длину? Ну, векторы могут помочь упростить нашу проблему.
Шаг 2: Линия Нормальная
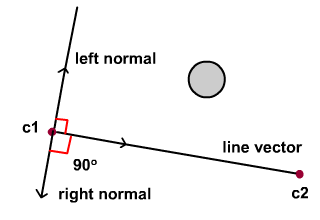
Чтобы нарисовать линию на сцене, нам нужны две координаты (c1 и c2). Линия, проведенная от c1 до c2, сформирует вектор, указывающий на c2 (обратите внимание на направление стрелки).
Далее нам нужно найти строку нормальную . Нормальная линия — это другая линия, которая составляет 90 ° с исходной линией и пересекается с ней в точке. Несмотря на то, что нормаль линии является еще одной линией, векторную форму нормали можно далее идентифицировать как левую или правую нормаль по отношению к вектору линии. Левая нормаль — это сам вектор линии, повернутый на -90 °. Правая норма та же самая, но повернута на 90 °. Помните, что ось Y в координатном пространстве Flash инвертирована по сравнению с осью Y на типичном графике, поэтому положительное вращение происходит по часовой стрелке, а отрицательное вращение против часовой стрелки.
Шаг 3: Проекция на левую нормаль
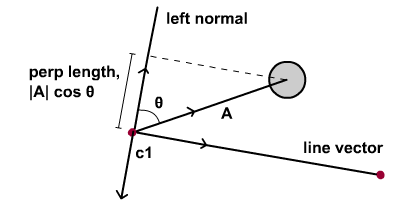
Левая нормаль используется в нашей попытке вычислить перпендикулярную длину между кругом и линией. Подробности можно найти на диаграмме ниже. A относится к вектору, указывающему от c1 до круга. Перпендикулярная длина на самом деле относится к проекции вектора А на левую нормаль. Мы выводим эту проекцию с помощью тригонометрии: это |A| Cosine (theta) |A| Cosine (theta) , где |A| относится к величине вектора А.
Самый простой подход — использовать векторные операции , в частности, скалярное произведение. Исходя из уравнения скалярного произведения , мы переставляем термины так, чтобы мы получили второе выражение, показанное ниже. Обратите внимание, что правая часть второго уравнения — это проекция, которую мы хотели вычислить!

Также обратите внимание, что левая и правая части уравнения в конечном итоге приведут к одному и тому же результату, хотя и будут разными. Таким образом, вместо использования правой части уравнения, мы можем выбрать левую часть уравнения. Чтобы легко получить конечный результат, выгодно использовать левый, потому что переменные могут быть легко разрешены. Если мы будем настаивать на использовании права уравнения, нам придется продвигать ActionScript через сложную математическую работу по вычислению угла тета. Мы заключаем с диаграммой ниже.
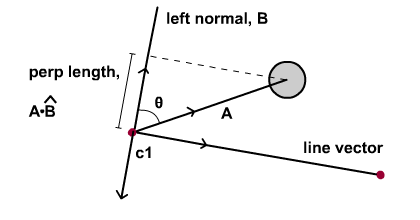
(* Дополнительное примечание: если окружность падает ниже линейного вектора, перпендикулярная длина, рассчитанная по формуле на приведенной выше диаграмме, будет давать отрицательное значение.)
Шаг 4: Реализация обнаружения столкновений по окружности
Теперь, когда мы поняли этот подход математически, давайте приступим к его реализации в ActionScript. В этом первом разделе обратите внимание, что вектор линии поворачивается на -90 °, образуя левую нормаль.
|
01
02
03
04
05
06
07
08
09
10
11
|
//declaring coordinates
x1 = 50;
x2 = 250;
//drawing line
graphics.lineStyle(3);
graphics.moveTo(x1, y1);
//forming line vectors
line = new Vector2D(x2 — x1, y2 — y1);
leftNormal = line.rotate(Math.PI * -0.5);
|
Во втором разделе я выделил упомянутые вычисления и условие проверки на наличие столкновения между окружностью и линией.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
|
private function refresh(e:Event):void {
for (var i:int = 0; i < circles.length; i++) {
//calculating line’s perpendicular distance to ball
var c1_circle:Vector2D = new Vector2D(circles[i].x — x1, circles[i].y — y1);
var c1_circle_onNormal:Number = c1_circle.projectionOn(leftNormal);
circles[i].y += 2;
//if collision happened, undo movement
if (Math.abs(c1_circle_onNormal) <= circles[i].radius){
circles[i].y -= 2;
}
}
}
|
Для тех, кто хотел бы продолжить исследование, ниже приведены выдержки из методов, используемых в Vector.as
|
1
2
3
4
5
6
7
8
9
|
/**
* Method to obtain the projection of current vector on a given axis
* @param axis An axis where vector is projected on
* @return The projection length of current vector on given axis
*/
public function projectionOn(axis:Vector2D):Number
{
return this.dotProduct(axis.normalise())
}
|
|
01
02
03
04
05
06
07
08
09
10
11
|
/**
* Method to perform dot product with another vector
* @param vector2 A vector to perform dot product with current vector
* @return A scalar number of dot product
*/
public function dotProduct(vector2:Vector2D):Number
{
var componentX:Number = this._vecX * vector2.x;
var componentY:Number = this._vecY * vector2.y;
return componentX+componentY;
}
|
|
1
2
3
4
5
6
7
8
|
/**
* Method to obtain vector unit of current vector
* @return A copy of normalised vector
*/
public function normalise():Vector2D
{
return new Vector2D(this._vecX/this.getMagnitude(), this._vecY/this.getMagnitude())
}
|
|
1
2
3
4
5
6
7
8
|
/**
* Method to obtain current magnitude of vector
* @return Magnitude of type Number
*/
public function getMagnitude():Number
{
return Math.sqrt(_vecX * _vecX + _vecY * _vecY);
}
|
Шаг 5: Результат
Нажмите кнопку «Перезагрузить», чтобы переместить все круги в верхней части сцены. Обратите внимание, что столкновение происходит между всей линией (включая не нарисованный участок) и кругами. Чтобы ограничить столкновение только сегментом линии, следите за обновлениями для следующего Быстрого совета.
Вывод
Спасибо за прочтение. Оставайтесь с нами для следующего совета.